Free space management in Operating System
Last Updated :
14 Apr, 2023
Introduction:
Free space management is a critical aspect of operating systems as it involves managing the available storage space on the hard disk or other secondary storage devices. The operating system uses various techniques to manage free space and optimize the use of storage devices. Here are some of the commonly used free space management techniques:
- Linked Allocation: In this technique, each file is represented by a linked list of disk blocks. When a file is created, the operating system finds enough free space on the disk and links the blocks of the file to form a chain. This method is simple to implement but can lead to fragmentation and wastage of space.
- Contiguous Allocation: In this technique, each file is stored as a contiguous block of disk space. When a file is created, the operating system finds a contiguous block of free space and assigns it to the file. This method is efficient as it minimizes fragmentation but suffers from the problem of external fragmentation.
- Indexed Allocation: In this technique, a separate index block is used to store the addresses of all the disk blocks that make up a file. When a file is created, the operating system creates an index block and stores the addresses of all the blocks in the file. This method is efficient in terms of storage space and minimizes fragmentation.
- File Allocation Table (FAT): In this technique, the operating system uses a file allocation table to keep track of the location of each file on the disk. When a file is created, the operating system updates the file allocation table with the address of the disk blocks that make up the file. This method is widely used in Microsoft Windows operating systems.
- Volume Shadow Copy: This is a technology used in Microsoft Windows operating systems to create backup copies of files or entire volumes. When a file is modified, the operating system creates a shadow copy of the file and stores it in a separate location. This method is useful for data recovery and protection against accidental file deletion.
Overall, free space management is a crucial function of operating systems, as it ensures that storage devices are utilized efficiently and effectively.
The system keeps tracks of the free disk blocks for allocating space to files when they are created. Also, to reuse the space released from deleting the files, free space management becomes crucial. The system maintains a free space list which keeps track of the disk blocks that are not allocated to some file or directory. The free space list can be implemented mainly as:
- Bitmap or Bit vector – A Bitmap or Bit Vector is series or collection of bits where each bit corresponds to a disk block. The bit can take two values: 0 and 1: 0 indicates that the block is allocated and 1 indicates a free block. The given instance of disk blocks on the disk in Figure 1 (where green blocks are allocated) can be represented by a bitmap of 16 bits as: 0000111000000110.
 Advantages –
Advantages –
- Simple to understand.
- Finding the first free block is efficient. It requires scanning the words (a group of 8 bits) in a bitmap for a non-zero word. (A 0-valued word has all bits 0). The first free block is then found by scanning for the first 1 bit in the non-zero word.
- Linked List – In this approach, the free disk blocks are linked together i.e. a free block contains a pointer to the next free block. The block number of the very first disk block is stored at a separate location on disk and is also cached in memory.
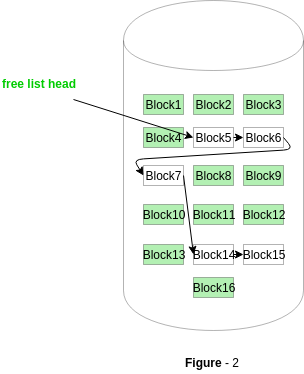 In Figure-2, the free space list head points to Block 5 which points to Block 6, the next free block and so on. The last free block would contain a null pointer indicating the end of free list. A drawback of this method is the I/O required for free space list traversal.
In Figure-2, the free space list head points to Block 5 which points to Block 6, the next free block and so on. The last free block would contain a null pointer indicating the end of free list. A drawback of this method is the I/O required for free space list traversal.
- Grouping – This approach stores the address of the free blocks in the first free block. The first free block stores the address of some, say n free blocks. Out of these n blocks, the first n-1 blocks are actually free and the last block contains the address of next free n blocks. An advantage of this approach is that the addresses of a group of free disk blocks can be found easily.
- Counting – This approach stores the address of the first free disk block and a number n of free contiguous disk blocks that follow the first block. Every entry in the list would contain:
- Address of first free disk block
- A number n
Here are some advantages and disadvantages of free space management techniques in operating systems:
Advantages:
- Efficient use of storage space: Free space management techniques help to optimize the use of storage space on the hard disk or other secondary storage devices.
- Easy to implement: Some techniques, such as linked allocation, are simple to implement and require less overhead in terms of processing and memory resources.
- Faster access to files: Techniques such as contiguous allocation can help to reduce disk fragmentation and improve access time to files.
Disadvantages:
- Fragmentation: Techniques such as linked allocation can lead to fragmentation of disk space, which can decrease the efficiency of storage devices.
- Overhead: Some techniques, such as indexed allocation, require additional overhead in terms of memory and processing resources to maintain index blocks.
- Limited scalability: Some techniques, such as FAT, have limited scalability in terms of the number of files that can be stored on the disk.
- Risk of data loss: In some cases, such as with contiguous allocation, if a file becomes corrupted or damaged, it may be difficult to recover the data.
- Overall, the choice of free space management technique depends on the specific requirements of the operating system and the storage devices being used. While some techniques may offer advantages in terms of efficiency and speed, they may also have limitations and drawbacks that need to be considered.
Share your thoughts in the comments
Please Login to comment...