Complementation process in DFA
Last Updated :
26 Jul, 2021
Prerequisite – Design a Finite automata
Suppose we have a DFA that is defined by ( Q, 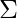 ,
, 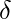 , q0, F ) and it accepts the language L1. Then, the DFA which accepts the language L2 where L2 = ̅L1‘, will be defined as below:
, q0, F ) and it accepts the language L1. Then, the DFA which accepts the language L2 where L2 = ̅L1‘, will be defined as below:
( Q, 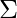 ,
, 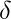 , q0, Q-F )
, q0, Q-F )
The complement of a DFA can be obtained by making the non-final states as final states and vice-versa. The language accepted by the complemented DFA L2 is the complement of the language L1.
Example-1:
L1: set of all strings over {a, b} of even length
L1 = {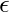 , ab, aa, abaa, aaba, ....}
, ab, aa, abaa, aaba, ....}
L2: set of all strings over {a, b} of odd length
L2 = { a, b, aab, aaa, bba, bbb, ...}
Here, we can see that L2 = ̅L1
Lets first draw the DFA for L1 that accepts the strings of even length.

Now, for designing the DFA for L2, we just need to complement the above DFA. We will change the non-final states as final state and the final states as non-final states.

This is our required complemented DFA.
Example-2:
L1: set of all strings over {a, b} starting with ‘a’.
L1 ={ a, ab, aa, aba, aaa, aab, ..}
L2: set of all strings over {a, b} not starting with ‘a’.
L2 ={ 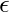 , b, ba, bb, bab, baa, bba, ...}
, b, ba, bb, bab, baa, bba, ...}
Here, we can see that L2 = ̅L1
Lets first draw the DFA for L1 that accepts the set of all strings over {a, b} starting with ‘a’

Now, for designing the DFA for L2, we just need to complement the above DFA. We will change the non-final states as final state and the final states as non-final states.

This is our required complemented DFA that accepts the strings that are not starting with ‘a’.
Note: Regular languages are closed under complement (i.e Complement of regular language will also be regular).
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...