Class 10 RD Sharma Solutions – Chapter 8 Quadratic Equations – Exercise 8.6 | Set 2
Last Updated :
16 May, 2021
Question 11. If – 5 is a root of the quadratic equation 2x² + px – 15 = 0 and the quadratic equation p(x² + x) + k = 0 has equal-roots, find the value of k.
Solution:
2x² + px – 15 = 0
-5 is its one root
It will satisfy it
2(-5)2+p(-5)-15=0
2*25-5p-15=0
50-15-5p=0
-5p+35=0
-5p=-35
p=-35/-5=7
Now in equation
p(x2+x)+k=0
7(x2+x)+k=0
7x2+7x+k=0
Here, a=7, b=7, c=k
D or b2-4ac = (7)2-4*7*k
=49-28k
Roots are real and equal
D or b2-4ac=0
49-28k=0⇒28k=49
k=49/28=7/4
Question 12. If 2 is a root of the quadratic equation 3x² + px – 8 = 0 and the quadratic equation 4x² – 2px + k = 0 has equal roots, find the value of k.
Solution:
2 is a root of 3x2+px-8=0
It will satisfy if
3(2)2+p*2-8=0
12+2p-8=0
4+2p=0
2p=-4
p=-4/2=-2
p=-2
Now in equation,
4x2-2px+k=0
4x2-2*(-2)x+k=0
4x2+4x+k=0
Here, a=4, b=4, c=k
D=b2-4ac=(4)2-4*4*k
=16- 16k
Roots are real and equal
D or b2-4ac=0
16-16k=0
=> 16k = 16
k = 16
Question 13. If 1 is a root of the quadratic equation 3x² + ax – 2 = 0 and the quadratic equation a(x² + 6x) – b=0 has equal roots, find the value of b.
Solution:
1 is one root of
3x² + ax – 2 = 0
3(1)2+a*1-2=0
3+a-2=0⇒a+1=0
a=-1
Now in equation a(x2+6x)-b=0
-1(x2+6x)-b=0
-x2-6x-b=0
⇒x2+6x+b=0
Here, a=1, b=6, c=b
D=b2-4ac=(6)2-4*1*k
=36-4k
Roots are equal
D or b2-4ac=0
36-4k=0
4k=-36
k=-36/4=-9
Question 14. Find the value of p for which the quadratic equation (p + 1) x² – 6 (p + 1) x + 3 (p + q) = 0, p ≠ -1 has equal roots. Hence, find the roots of the equation.
Solution:
(p+1)x2-6(p+1)x+3(p+9)=0,
p≠-1
Comparing with ax2+bx+c=0
b2-4ac, c=p+1, b=-6(p+1), c=3(p+9)
Now D=b2-4ac
=[-6(p+1)]2-4*(p+1)*3(p+9)
=36(p+9)2-12(p+1)(p+9)
Roots are equal
D=0
⇒36(p+1)2-12(p+1)(p+9)=0
⇒36(p+1)2=12(p+1)(p+9)
⇒3(p+1)=p+9⇒3p+3=p+9
⇒3p-p=⇒9-3⇒2p=6
p=6/2=3
p=3
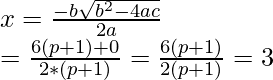
Hence, x=3,3
Question 15. Determine the nature of the roots of the following quadratic equations :
(i) (x – 2a) (x – 2b) = 4ab
Solution:
⇒x2-2bx-2ax+4ab-4ab=0
Here, a=1,b=-2(a+b), c=0
Discriminant(D)=b2-4ac
={-2(a+b)}2-4*1*0
={-2(a+b)}2
D>0
Roots are real and distinct
(ii) 9a²b²x² – 24abcdx + 16c²d² = 0, a ≠ 0, b ≠ 0
Solution:
Here a=9a2b2, b=-24abcd, c=16c2d2
D=b2-4ac
=(-24abcd)2-4*9a2b2*16c2d2
=576a2b2c2d2-576a2b2c2d2
=0
D=0
Roots are real and equal
(iii) 2 (a² + b²) x² + 2 (a + b) x + 1 = 0
Solution:
Here a=2(a2+b2), b=2(a+b), c=1
D=b2-4ac
={2(a+b)}2-4*2(a2+b2)*1
=4(a2+b2+2ab)-8(a2+b2)
=4a2+4b2+8ab-8a2-8b2
=8ab-4a2-4b2
=-(4a2+4b2-8ab)
=-4(a2+b2-2ab)
=-4(a-b)2
D<0
Root are not real
(iv) (b + c) x² – (a + b + c) x + a = 0
Solution:
Here a=b+c, b=-(a+b+c), c=a
D=b2-4ac
=[-(a+b+c)]2-4*(b+c)*a
=a2+b2+c2+2ab+2bc+2ca=4ab-4ca
=a2+b2+c2-2ab+2bc-2ca
=[-a+b+c]2
D>0
Roots are real and distinct.
Question 16. Determine the set of values of k for which the given following quadratic equation has real roots :
(i) x² – kx + 9 = 0
Solution:
Here a=1, b=-k, c=9
D=b2-4ac
=(-k)2-4*1*9
=k2-36
Roots are real
D≥⇒k2-36≥0
k2≥36⇒k2(±6)2
k≥6 or k≤-6
(ii) 2x² + kx + 2 = 0
Solution:
Here, a=2, b=k, c=2
D=b2-4ac
=(k)2-4*2*2
=k2-16
Roots are real
D≥0⇒k2-16≥0
k2≥16⇒(k)2≥(±4)2
k≥4 or k≤-4
(iii) 4x² – 3kx +1=0
Solution:
Here a=4, b=-3k, c=1
D=b2-4ac
=(-3k)2-4*4*1
=9k2-16
Roots are real
D≥0⇒9k2-16≥0
9k2≥16⇒k2≥16/9
(k)2≥(±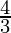 )2
)2
k≥4/3 or k≤-4/3
(iv) 2x² + kx – 4 = 0
Solution:
Here a=2, b=k, c=-4
D=b2-4ac
=k2-4*2*(-4)
=k2+32
The roots are real
D≥0⇒k2+32≥0
k2+32≥0 for all value of
k ∈ R
Question 17. If the roots of the equation (b – c) x² + (c – a) x + (a – b) = 0 are equal, then prove that 2b = a + c. [CBSE 2002C]
Solution:
(b – c) x² + (c – a) x + (a – b) = 0
Here a=b-c, B=c-a, c=a-b
D=b2-4ac
=(c-a)2-4(b-c)(a-b)
The roots are equal
D=0
(c-a)2-4(b-c)(a-b)=0
c2+a2-2ca-4(ab-b2-ca+bc)=0
c2+a2-2ca-4ab+4b2+4ca-4bc=0
a2+4b2+c2-4ab-4bc+2ca=0
(a-2b+c)2=0⇒a-2b+c=0
=> a + c = 2b
=> 2b = a + c
Hence proved.
Question 18. If the roots of the equation (a² + b²) x² – 2 (ac + bd) x + (c² + d²) = 0 are equal. prove that ab = cd
Solution:
Here a=a² + b², b= – 2 (ac + bd), c=c² + d²
D=b2-4ac
=[-2(ac+bd)]2-4(a2+b2)(c2+d2)
=4(ac+bd)2-4[a2c2+a2d2+b2c2+b2d2]
=4[a2c2+b2d2+2abcd]-4[a2c2+a2d2+b2c2+b2d2]
=4a2c2+4b2d2+8abcd-4a2d2-4b2c2-4b2d2
=8abcd-4a2d2-4b2c2
The roots are equal
D=0
8abcd-4a2d2-4b2c2=0
a2d2+b2c2-2abcd=0 ———–(Dividing by -4)
(ad-bc)2=0⇒ad-bc=0
ad=bc⇒a/b=c/d
Question 19. If the roots of the equations ax² + 2bx + c = 0 and bx² – 2√ac x + b = 0 are simultaneously real, then prove that b² = ac
Solution:
ax2+2bx+c=0 ———–(i)
and bx2-2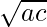 x+b=0 ———–(ii)
x+b=0 ———–(ii)
Let D1 and D2 are the discriminants of there simultaneous equation (i) and (ii)
D1=(2b)2-4*a*c=4b2-4ac
and D2=(-2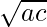 )2-4*b*b
)2-4*b*b
=4ac=4b2
These have real roots
D1≥0⇒4b2-4ac≥0
⇒4b2≥4ac⇒b2≥ac ————-(i)
and D2≥0
Therefore, 4ac-4b2≥0 ⇒4ac≥4b2
ac ≥ b2 ——————(ii)
ac≥b2≥ac
b2=ac
Question 20. If p, q are real and p ≠ q, then show that the roots of the equation (p – q) x² + 5(p + q) x – 2(p – q) = 0 are real and unequal.
Solution:
Here a=p-q, b=5(p+q), c=-2(p-q)
D=b2-4ac
=[5(p+q)]2-4*(p-q)*-2(p-q)
=25(p+q)2+8(p-q)2
p and q are real and p≠q
25(p+q)2+8(p-q)≥0
The given quadratic equation has real and unequal roots.
Question 21. If the roots of the equation (c² – ab) x² – 2 (a² – bc) x + b² – ac = 0 are equal, prove that either a = 0 or a3 + b3 + c3 = 3abc.
Solution:
Here a=c2-ab, b=-2(a2-bc), c=b2-ac
D=b2-4ac
=[-2(a2-bc)]2-4(c2-ab)(b2-ac)
=4[a4+b2c2-2a2bc]-4[b2c2-ac3-ab3+a2bc]
=4a4+4b2c2-8a2bc-4b2c2+4ac3+4ab3-4ac2bc
=4a4+4ab+4ac3-12a2bc
=4a[a3+b3+c3-3abc]
D=0
4a(a3+b3+c3-3abc)=0
a(a3+b3+c3-3abc)=0
Either a=0
or a3+b3+c3=3abc=0
a3+b3+c3=3abc
Question 22. Show that the equation 2 (a² + b²) x² + 2 (a + b) x + 1 = 0 has no real roots, when a ≠ b.
Solution:
Here a=2(a+b2), b=2(a+b), c=1
D=b2-4ac
[2(a+b)]2-4*2*(a2+b2)*1
4(a+b2+2ab)-8(a2+b2)
=4a2+4b2+8ab-8a2-8b2
=-4a2-b2+8ab
-4[a2+b2-2ab]
=-4(a-b)2
D<0
Roots are not real
Question 23. Prove that both the roots of the equation (x – a) (x – b) + (x – b) (x – c) + (x – c) (x – a) = 0 are real but they are equal only when a = b = c.
Solution:
Here a=3, b=-2(a+b+c), c=ab+ac+ca
D=b2-4ac
=[-2(a+b+c)]2-4*3(ab+bc+ca)
=4(a+b+c)2-12(ab+bc+ca)
=4[(a+b+c)]2-3(ab+bc+ca)
=4[a2+b2+c2+2ab+2bc+2ca-3ab-3bc-3ca]
=2[(a-b)]2+(b-c)2+(c-a)2]
Clearly, D≥0
Roots are real
If roots are equal, then
D=0
(a-b)2+(b-c)2+(c-a)2=0
a-b=0, b-c=0, c-a=0
a=b=, b=c, c=a
a=b=c
Hence proved
Question 24. If a, b, c are real numbers such that ac ≠ 0, then show that at least one of the equations ax² + bx + c = 0 and – ax² + bx + c = 0 has real roots.
Solution:
a,b,c are real number
and ac≠0
ax2+bx+c=0 ———-(i)
-ax+bx+c=0 ——–(ii)
Let D1 and D2 be the discriminants of the two equation (i) and (ii)
D1= b2-4ac and D2=b2-4ac
If equation (i) has real roots, then
D1≥0
b2-4ac≥0
b2-≥ac
Now D2=b2+4ac
4ac≤b2
b2+4ac≥0
D≥0
Both the equation has real roots
Hence proved
Question 25. If the equation (1 + m²) x² + 2mcx + (c² – a²) = 0 has equal roots, prove that c² = a² (1 + m²).
Solution:
Here a=1+m2, b=2mc, c=c2-a2
D=b2-4ac
=(2mc)2-4(1+m2)(c2-a2)
=4m2c2-4c2+4a-4m2c2+4m2a2
=4a2+4m2a2-4c2
Root are equal
D=0⇒4a2+4m2a2-4c2=0
a2+m2a2-c2=0
a2+m2a2=c2
a2(a+m2)=c2
c2=a2(1+m2)
Hence proved
Share your thoughts in the comments
Please Login to comment...