Class 10 RD Sharma Solutions – Chapter 8 Quadratic Equations – Exercise 8.4
Last Updated :
30 Apr, 2021
Question 1: Find the roots of the following quadratic (if they exist) by the method of completing the square: 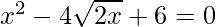 .
.
Solution:
Given: 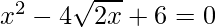
We have to make the equation a perfect square.
=> 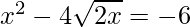
=> 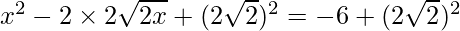
We know that:
=> (a−b)2 = a2−2×a×b+b2
Thus, the equation can be written as:
=> 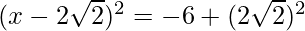
=> 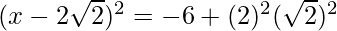
=> 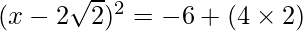
=> 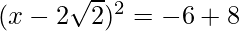
=> 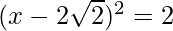
The RHS is positive, which implies that the roots exist.
=> 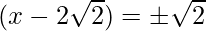
=> x = 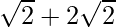 and x=
and x= 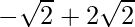
=> x = 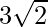 and x =
and x = 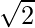
Question 2: Find the roots of the following quadratic (if they exist) by the method of completing the square: 2x2-7x+3 = 0.
Solution:
Given: 2x2-7x+3 = 0
We have to make the equation a perfect square.
=> 2x2-7x+3 = 0
=> 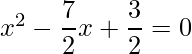
=> 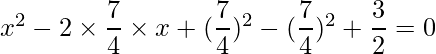
We know that:
=> (a−b)2=a2−2×a×b+b2
Thus, the equation can be written as:
=> 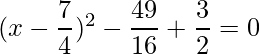
=> 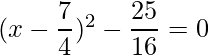
=> 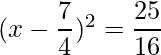
The RHS is positive, which implies that the roots exist.
=> 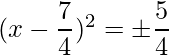
=> 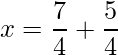 and
and 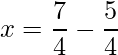
=> 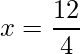 and
and 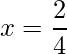
=> x = 3 and 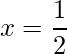
Question 3: Find the roots of the following quadratic (if they exist) by the method of the completing the square: 3x2+11x+10 = 0.
Solution:
Given: 3x2+11x+10 = 0
We have to make the equation a perfect square.
=> 3x2+11x+10 = 0
=> 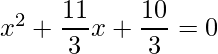
=> 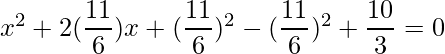
We know that:
=> (a−b)2=a2−2×a×b+b2
Thus the equation can be written as:
=> 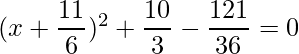
=> 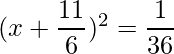
The RHS is positive, which implies that the roots exist.
=> 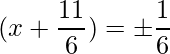
=> 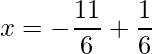 and
and 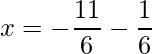
=> 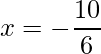 and
and 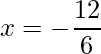
=> 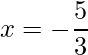 and x = -2
and x = -2
Question 4: Find the roots of the following quadratic (if they exist) by the method of completing the square: 2x2+x-4 =0.
Solution:
Given: 2x2+x-4 =0
We have to make the equation a perfect square.
=> 2x2+x-4 =0
=> 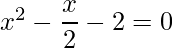
=> 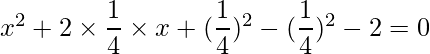
We know that:
=> (a−b)2=a2−2×a×b+b2
Thus the equation can be written as:
=> 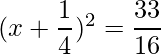
The RHS is positive, which implies that the roots exist.
=>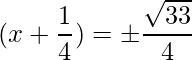
=> 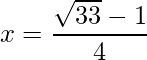 and
and 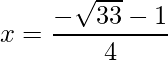
Question 5: Find the roots of the following quadratic (if they exist) by the method of completing the square: 2x2+x+4 =0.
Solution:
Given: 2x2+x+4 =0
We have to make the equation a perfect square.
=> 2x2+x+4 =0
=> 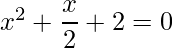
=> 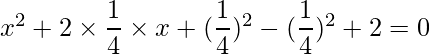
We know that:
=> (a−b)2=a2−2×a×b+b2
Thus the equation can be written as:
=> 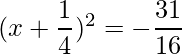
=> The RHS is negative, which implies that the roots are not real.
Question 6: Find the roots of the following quadratic (if they exist) by the method of completing the square: 4x2+4√3+3=0.
Solution:
Given: 4x2+4√3+3=0
We have to make the equation a perfect square.
=> 4x2+4√3+3=0
=> 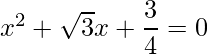
=> 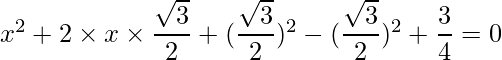
We know that,
=> (a−b)2=a2−2×a×b+b2
Thus the equation can be written as:
=> 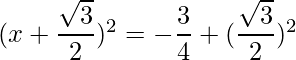
=> 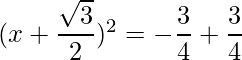
=> 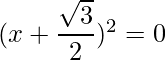
The RHS is zero, which implies that the roots exist and are equal.
=> 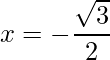
Question 7: Find the roots of the following quadratic (if they exist) by the method of the completing the square: 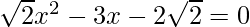 .
.
Solution:
Given: 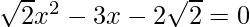
We have to make the equation a perfect square.
=> 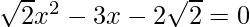
=> 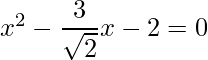
=> 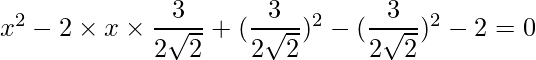
We know that,
=> (a−b)2=a2−2×a×b+b2
Thus the equation can be written as:
=> 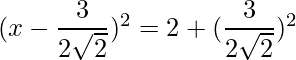
=> 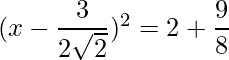
=> 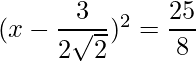
The RHS is positive, which implies that the roots exist.
=> 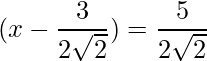
=> 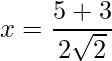 and
and 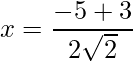
=> 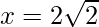 and
and 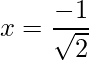
Question 8: Find the roots of the following quadratic (if they exist) by the method of completing the square: 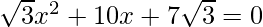 .
.
Solution:
Given: 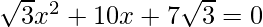
We have to make the equation a perfect square.
=> 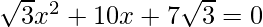
=> 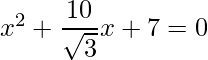
=> 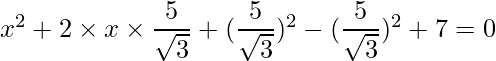
We know that,
=> (a−b)2=a2−2×a×b+b2
Thus the equation can be written as:
=> 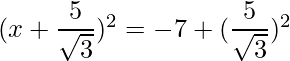
=> 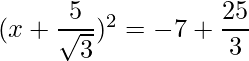
=> 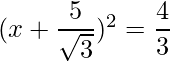
The RHS is positive, which implies that the roots exist.
=> 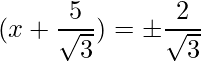
=> 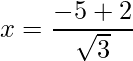 and
and 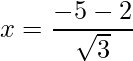
=> 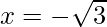 and
and 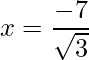
Question 9: Find the roots of the following quadratic (if they exist) by the method of completing the square: 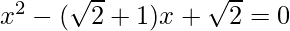 .
.
Solution:
Given: 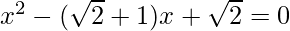
We have to make the equation a perfect square.
=> 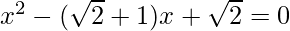
=> 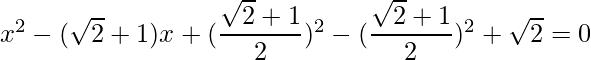
We know that,
=> (a−b)2=a2−2×a×b+b2
Thus the equation can be written as:
=> 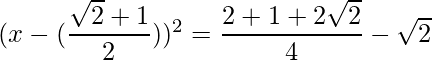
=> 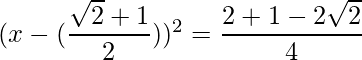
=> 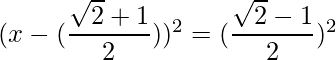
The RHS is positive, which implies that the roots exist.
=> 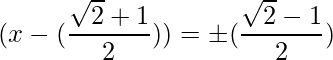
=> 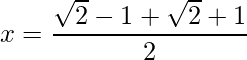 and
and 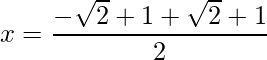
=> x = √2 and x = 1
Question 10: Find the roots of the following quadratic equation (if they exist) by the method of completing the square: x2-4ax+4a2-b2=0.
Solution:
Given: x2-4ax+4a2-b2=0
We have to make the equation a perfect square.
=> x2-4ax+4a2-b2=0
=> x2−2×x×2a+(2a)2−b2=0
We know that,
=> (a−b)2=a2−2×a×b+b2
Thus the equation can be written as:
=> x2−2×2a×x+(2a)2=b2
=> (x-2a)2 = b2
The RHS is positive, which implies that the roots exist.
=> (x-2a) = ±b
=> x= 2a+b and x = 2a-b
Share your thoughts in the comments
Please Login to comment...