Class 10 RD Sharma Solutions – Chapter 7 Statistics – Exercise 7.5 | Set 2

Read

Discuss

Question 11. Find the mean, median, and mode of the following data:

Classes	0-50	50-100	100-150	150-200	200-250	250-300	300-350
Frequency	2	3	5	6	5	3	1

Solution:

Let mean (A) = 175

Classes
Class Marks

(x)

Frequency

(f)
c.f.
d_i = x – A

A = 175
f_i * d_i

0-50 25 2 2 -150 -300

50-100 75 3 5 -100 -300

100-150 125 5 10 -50 -250

150-200 175-A 6 16 0 0

200-250 225 5 21 50 250

250-300 275 3 24 100 300

300-350 325 1 25 150 150

Total 25 -150

Find Median:

Here N = 25, 5/3 = 25/2 = 12.5 or 13, it lies in the class interval = 50-200.

l = 150, F = 10, f = 6, h = 50

Using median formula, we get

$Median = l + \frac{\frac{N}{2}-F}{f} * h \\ = 150 + \frac{12.5-10}{6} * 50 \\ = 150 + \frac{125}{6}$

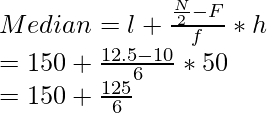
= 150 + 20.83

= 170.83

Find Mean:

Using mean formula we get

$Mean = A + \frac{\sum f d_i}{\sum f} \\ = 175 + \frac{-150}{25}$

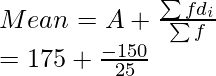
= 175 – 6

= 169

Find Mode:

Using mode formula we get

$Mode = l + \frac{f-f_1}{2f-f_1-f_2} * h \\ = 150 + \frac{6-5}{2*6-5-5} * 50$

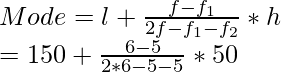
= 150 + 25

= 175

Question 12. A student noted the number of cars passing through a spot on a road for 100 periods each of 3 minutes and summarized it in the table given below. Find the mode of the data.

Number of cars	0-10	10-20	20-30	30-40	40-50	50-60	60-70	70-80
Frequency	7	14	13	12	20	11	15	8

Solution:

From the given table we conclude that

Modal class = 40-50 (it has maximum frequency)

Also,

l = 40, f = 20, f₁ = 12, f₂ = 11 and h = 10

By using mode formula, we get

$Mode = l + \frac{f-f_1}{2f-f_1-f_2} * h \\ = 40 + \frac{20-12}{2*20-12-11} * 10 \\ = 40 + \frac{8*10}{40-23} \\ = 40 + \frac{8*10}{17}$

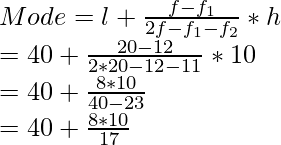
= 40 + 4.70

= 44.7

Question 13. The following frequency distribution gives the monthly consumption of electricity of 68 consumers of a locality. Find the median, mean, and mode of the data and compare them:

Monthly consumption(in units)	65-85	85-105	105-125	125-145	145-165	165-185	185-205
No. of consumers	4	5	13	20	14	8	4

Solution:

Let mean (A) = 135

Monthly consumption Class Marks (x) No. of consumers (f) c.f. d = x – A f.d

65-85 75 4 4 -60 -240

85-105 95 5 9 -40 -200

105-125 115 13 22 -20 -260

125-145 135 20 42 0 0

145-165 155 14 56 20 280

165-185 175 8 64 40 320

185-205 195 4 68 60 240

Total 68 140

Find Median:

Here, N = 34

N/2 = 34,

Class interval = 25-145

Also,

l = 125, F = 22, f = 20 and h = 20

By using the median formula, we get

$Median = l + \frac{\frac{N}{2}-F}{f} * h \\ = 125 + \frac{34-22}{20} * 20$

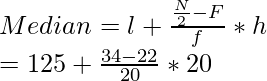
= 125 + 12

= 137 units

Find Mean:

By using the mean formula, we get

Mean = 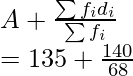$A + \frac{\sum f_id_i}{\sum f_i} \\ = 135 + \frac{140}{68}$

= 135 + 2.05

= 137.05 units

Find Mode:

By using the mode formula, we get

$Mode = l + \frac{f-f_1}{2f-f_1-f_2} * h \\ = 125 + \frac{20-13}{2*20-14-13} * 10 \\ = 125 + \frac{7*20}{40-27} \\ = 125 + \frac{140}{13}$

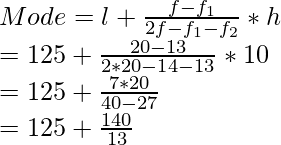
= 125 + 10.76

= 135.76 units

Question 14. 100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows:

Number of letters	1-4	4-7	7-10	10-13	13-16	16-19
Number of surnames	6	30	40	16	4	4

Determine the median number of letters in the surnames. Find the mean number of letters in the surnames. Also, And the modal size of the surnames.

Solution:

Let mean (A) = 8.5

Number of letters Class Marks(x) No. of surnames (f) c.f. d = x- A f.d.

1-4 2.5 6 6 -6 -36

4-7 5.5 30 36 -3 -90

7-10 8.5-A 40 76 0 0

10-13 11.5 16 92 3 48

13-16 14.5 4 96 6 24

16-19 17.5 4 100 9 36

Total 100 -18

Find Median:

Here, N = 100

So, N/2 = 50

Class interval = 7-10

l = 7, F = 36, f = 40 and h =3

By using the median formula, we get

$Median = l + \frac{\frac{N}{2}-F}{f} * h \\ = 7 + \frac{50-36}{40} * 3 \\ = 7 + \frac{14}{40} * 3$

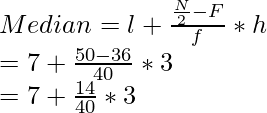
= 7 + 1.05

= 8.05

Find Mean:

By using the mean formula, we get

Mean = 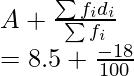$A + \frac{\sum f_id_i}{\sum f_i} \\ = 8.5 + \frac{-18}{100}$

= 8.5 + 0.18

= 8.32

Find Mode:

We have,

N = 100

N/2 = 100/2 = 50

Here, the cumulative frequency is just greater than N/2 = 76,

Hence, the median class = 7 – 10

l = 7, h = 10 – 7 = 3, f = 40, F = 36

By using the mode formula, we get

Mode = l + 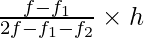$\frac{f-f_1}{2f-f_1-f_2}\times h$

= 7 + $\frac{40-30}{2\times40-30-16}\times3$

= 7 + 30/34

= 7 + 0.88

= 7.88

Question 15. Find the mean, median, and mode of the following data:

Class	0 – 20	20 – 40	40 – 60	60 – 80	80 – 100	100 – 120	120 – 140
Frequency	6	8	10	12	6	5	3

Solution:

Class interval Mid value Frequency (f) fx Cumulative frequency

0 – 20 10 6 60 6

20 – 40 30 8 240 17

40 – 60 50 10 500 24

60 – 80 70 12 840 36

80 – 100 90 6 540 42

100 – 120 110 5 550 47

120 – 140 130 3 390 50

N = 50 ∑fx = 3120

Find Mean:

By using the mean formula, we get

Mean = 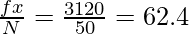$\frac{∑fx}{N}=\frac{3120}{50}=62.4$

Find Median:

We have,

N = 50

Then, N/2 = 50/2 = 25

Here, the cumulative frequency just greater than N/2 = 36

Hence, the median class = 60 – 80

l = 60, h = 80 – 60 = 20, f = 12, F = 24

By using the median formula, we get

Median = l + 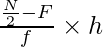$\frac{\frac{N}{2}-F}{f}\times h$

= 60 + $\frac{25-24}{12}\times20$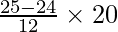

= 60 + 20/12

= 60 + 1.67

= 61.67

Find Mode:

We have,

The maximum frequency = 12

Model class = 60 – 80

l = 60, h = 80 – 60 = 20, f = 12, f₁ = 10, f₂ = 6

By using the mode formula, we get

Mode = l + 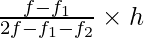$\frac{f-f_1}{2f-f_1-f_2}\times h$

= 60 + $\frac{12-10}{2× 12-10-6}\times 20$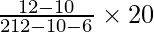

= 60 + 40/8

= 65

Question 16. The following data gives the distribution of total monthly household expenditure of 200 families of a village. Find the modal monthly expenditure of the families. Also, find the mean monthly expenditure:

Expenditure	Frequency	Expenditure	Frequency
1000 – 1500	24	3000 – 3500	30
1500 – 2000	40	3500 – 4000	22
2000 – 2500	33	4000 – 4500	16
2500 – 3000	28	4500 – 5000	7

Solution:

From the given table we conclude that

The maximum class frequency = 40

So, modal class = 1500 – 2000

l = 1500, f = 40, h = 500, f₁= 24, f₂= 33

By using the mode formula, we get

Mode = l + 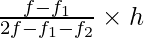$\frac{f-f_1}{2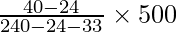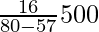f-f_1-f_2}\times h$

= 1500 + $\frac{40-24}{2× 40-24-33}\times500$

= 1500 + $\frac{16}{80-57}× 500$

= 1500 + 347.826

= 1847.826 ≈ 1847.83

Hence, the modal monthly expenditure = Rs. 1847.83

Now we will find class marks as

Class mark = 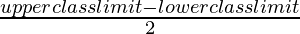$\frac{upperclasslimit-lowerclasslimit}{2}$

Class size (h) of given data = 500

Let mean(a) = 2750, now we are going to calculate d_iu_i as follows:

Expenditure (In Rs) Number of families f_i X_i d_i = x_i – 2750 U_i f_iu_i

1000 – 1500 24 1250 -1500 -3 -72

1500 – 2000 40 1750 -1000 -2 -80

2000 – 2500 33 2250 -500 -1 -33

2500 – 3000 28 2750 0 0 0

3000 – 3500 30 3250 500 1 30

3500 – 4000 22 3750 1000 2 44

4000 – 4500 16 4250 1500 3 48

4500 – 5000 7 4750 2000 4 28

Total 200 -35

From the table we conclude that

∑f_i= 200

∑f_id_i= -35

Mean 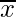$\overline{x}$ = a + $\frac{\sum f_id_i}{\sum f_i}\times h$

= 2750 + $\frac{-35}{200}\times500$

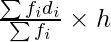
= 2750 – 87.5

= 2662.5

Hence, the mean monthly expenditure = Rs. 2662.5

Question 17. The given distribution shows the number of runs scored by some top batsmen of the world in one day international cricket matches.

Runs scored	No. of batsmen	Runs scored	No. of batsmen
3000 – 4000	4	7000 – 8000	6
4000 – 5000	18	8000 – 9000	3
5000 – 6000	9	9000 – 10000	1
6000 – 7000	7	10000 – 11000	1

Find the mode of the data

Solution:

From the given table we conclude that

The maximum class frequency = 18

So, modal class = 4000 – 5000

and

l = 4000, f = 18, h = 1000, f₁= 4, f₂= 9

By using the mode formula, we get

Mode = l + 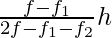$\frac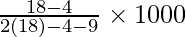{f-f_1}{2f-f_1-f_2}× h$

= 4000 + $\frac{18-4}{2(18)-4-9}\times 1000$

= 4000 + (14000/23)

= 4000 + 608.695

= 4608.695

Hence, the mode of given data = 4608.7 runs.

Question 18. The frequency distribution table of agriculture holdings in a village is given below:

Area of land (in hectares):	1 – 3	3 – 5	5 – 7	7 – 9	9 – 11	11 – 13
Number of families	20	45	80	55	40	12

Find the modal agriculture holdings of the village.

Solution:

From the given table we conclude that

The maximum class frequency = 80,

So, the modal class = 5-7

and

l = 5, f₀ = 45, h = 2, f₁= 80, f₂= 55

By using the mode formula, we get

Mode = l + 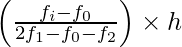$\left(\frac{f_i-f_0}{2f_1-f_0-f_2}\right)\times h$

= 5 + $\left(\frac{80-45}{2(80)-45-55}\right)\times 2$

= 5 + $\frac{35}{60}\times2$

= 5 + $\frac{35}{30}$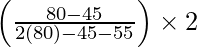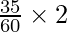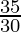

= 5 + 1.2

= 6.2

So, the modal agricultural holdings of the village = 6.2 hectares.

Question 19. The monthly income of 100 families are given as below:

Income in (in Rs)	Number of families
0 – 5000	8
5000 – 10000	26
10000 – 15000	41
15000 – 20000	16
20000 – 25000	3
25000 – 30000	3
30000 – 35000	2
35000 – 40000	1

Calculate the modal income.

Solution:

From the given table we conclude that

The maximum class frequency = 41,

So, modal class = 10000-15000.

Here, l = 10000, f₁ = 41, f₀ = 26, f₂ = 16 and h = 5000

Therefore, by using the mode formula, we get

Mode = l + 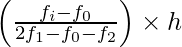$\left(\frac{f_i-f_0}{2f_1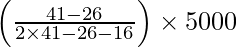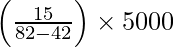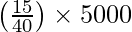-f_0-f_2}\right)\times h$

= 10000 + $\left(\frac{41-26}{2\times41-26-16}\right)\times 5000$

= 10000 + $\left(\frac{15}{82-42}\right)\times 5000$

= 10000 + $\left(\frac{15}{40}\right)\times 5000$

= 10000 + 15 × 125

= 10000 + 1875

= 11875

So, the modal income = Rs. 11875.

Whether you're preparing for your first job interview or aiming to upskill in this ever-evolving tech landscape, GeeksforGeeks Courses are your key to success. We provide top-quality content at affordable prices, all geared towards accelerating your growth in a time-bound manner. Join the millions we've already empowered, and we're here to do the same for you. Don't miss out - check it out now!

Last Updated : 05 Mar, 2021

Classes	Class Marks (x)	Frequency (f)	c.f.	d_i = x – A A = 175	*f_i d_i**
0-50	25	2	2	-150	-300
50-100	75	3	5	-100	-300
100-150	125	5	10	-50	-250
150-200	175-A	6	16	0	0
200-250	225	5	21	50	250
250-300	275	3	24	100	300
300-350	325	1	25	150	150
Total		25			-150

Monthly consumption	Class Marks (x)	No. of consumers (f)	c.f.	d = x – A	f.d
65-85	75	4	4	-60	-240
85-105	95	5	9	-40	-200
105-125	115	13	22	-20	-260
125-145	135	20	42	0	0
145-165	155	14	56	20	280
165-185	175	8	64	40	320
185-205	195	4	68	60	240
Total		68			140

Number of letters	Class Marks(x)	No. of surnames (f)	c.f.	d = x- A	f.d.
1-4	2.5	6	6	-6	-36
4-7	5.5	30	36	-3	-90
7-10	8.5-A	40	76	0	0
10-13	11.5	16	92	3	48
13-16	14.5	4	96	6	24
16-19	17.5	4	100	9	36
Total		100			-18

Class interval	Mid value	Frequency (f)	fx	Cumulative frequency
0 – 20	10	6	60	6
20 – 40	30	8	240	17
40 – 60	50	10	500	24
60 – 80	70	12	840	36
80 – 100	90	6	540	42
100 – 120	110	5	550	47
120 – 140	130	3	390	50
		N = 50	∑fx = 3120

Expenditure (In Rs)	Number of families f_i	X_i	d_i = x_i – 2750	U_i	f_iu_i
1000 – 1500	24	1250	-1500	-3	-72
1500 – 2000	40	1750	-1000	-2	-80
2000 – 2500	33	2250	-500	-1	-33
2500 – 3000	28	2750	0	0	0
3000 – 3500	30	3250	500	1	30
3500 – 4000	22	3750	1000	2	44
4000 – 4500	16	4250	1500	3	48
4500 – 5000	7	4750	2000	4	28
Total	200				-35

Chapter 1: Real Numbers

Chapter 2: Polynomials

Chapter 3: Pair of Linear Equations in Two Variables

Chapter 4: Triangles

Chapter 5: Trigonometric Ratios

Chapter 6: Trigonometric Identities

Chapter 7: Statistics

Chapter 8: Quadratic Equations

Chapter 9: Arithmetic Progressions

Chapter 10: Circles

Chapter 11: Constructions

Chapter 12: Some Applications of Trigonometry

Chapter 13: Probability

Chapter 14: Coordinate Geometry

Chapter 15: Areas Related To Circles

Chapter 16: Surface Areas And Volumes

Chapter 1: Real Numbers

Chapter 2: Polynomials

Chapter 3: Pair of Linear Equations in Two Variables

Chapter 4: Triangles

Chapter 5: Trigonometric Ratios

Chapter 6: Trigonometric Identities

Chapter 7: Statistics

Chapter 8: Quadratic Equations

Chapter 9: Arithmetic Progressions

Chapter 10: Circles

Chapter 11: Constructions

Chapter 12: Some Applications of Trigonometry

Chapter 13: Probability

Chapter 14: Coordinate Geometry

Chapter 15: Areas Related To Circles

Chapter 16: Surface Areas And Volumes

Class 10 RD Sharma Solutions – Chapter 7 Statistics – Exercise 7.5 | Set 2

Question 11. Find the mean, median, and mode of the following data:

Question 12. A student noted the number of cars passing through a spot on a road for 100 periods each of 3 minutes and summarized it in the table given below. Find the mode of the data.

Question 13. The following frequency distribution gives the monthly consumption of electricity of 68 consumers of a locality. Find the median, mean, and mode of the data and compare them:

Question 14. 100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows:

Determine the median number of letters in the surnames. Find the mean number of letters in the surnames. Also, And the modal size of the surnames.

Question 15. Find the mean, median, and mode of the following data:

Question 16. The following data gives the distribution of total monthly household expenditure of 200 families of a village. Find the modal monthly expenditure of the families. Also, find the mean monthly expenditure:

Question 17. The given distribution shows the number of runs scored by some top batsmen of the world in one day international cricket matches.

Find the mode of the data

Question 18. The frequency distribution table of agriculture holdings in a village is given below:

Find the modal agriculture holdings of the village.

Question 19. The monthly income of 100 families are given as below:

Calculate the modal income.

Please Login to comment...