Difference between Context Free Grammar and Regular Grammar
Last Updated :
31 May, 2021
Noam Chomsky has divided grammar into four types :
|
Type
|
Name
|
|
0
|
Unrestricted Grammar |
|
1
|
Context Sensitive Grammar |
|
2
|
Context Free Grammar |
|
3
|
Regular Grammar |
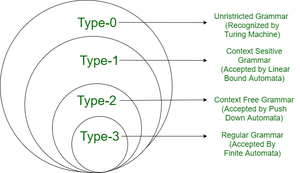
Chomsky Hierarchy
1. Context Free Grammar :
- Language generated by Context Free Grammar is accepted by Pushdown Automata
- It is a subset of Type 0 and Type 1 grammar and a superset of Type 3 grammar.
- Also called phase structured grammar.
- Different context-free grammars can generate the same context-free language.
- Classification of Context Free Grammar is done on the basis of the number of parse trees.
- Only one parse tree->Unambiguous.
- More than one parse tree->Ambiguous.
Productions are in the form –
A->B;
A∈N i.e A is a non-terminal.
B∈V*(Any string).
Example –
S –> AB
A –> a
B –> b
2. Regular Grammar :
- It is accepted by Finite State Automata.
- It is a subset of Type 0 ,Type 1 and Type 2 grammar.
- The language it generates is called Regular Language.
- Regular languages are closed under operations like Union, Intersection, Complement etc.
- They are the most restricted form of grammar.
Productions are in the form –
V –> VT / T (left-linear grammar)
(or)
V –> TV /T (right-linear grammar)
Example –
1. S –> ab.
2. S -> aS | bS | ∊
Difference Between Context Free Grammar and Regular Grammar:
| Parameter |
Context Free Grammar |
Regular Grammar |
| Type |
Type-2 |
Type-3 |
| Recognizer |
Push-down automata. |
Finite State Automata |
| Rules |
Productions are of the form:
A->B;
A∈N(Non-Terminal)
B∈V*(Any string) |
Productions are of the form:
V –> VT / T (left-linear grammar)
(or)
V –> TV /T (right-linear grammar) |
| Restriction |
Less than Regular Grammar |
More than any other grammar |
| Right-hand Side |
The right-hand side of production has no restrictions. |
The right-hand side of production should be either left linear or right linear. |
| Set Property |
Super Set of Regular Grammar |
Subset of Context Free Grammar |
| Intersection |
Intersection of two CFL need not be a CFL |
Intersection of two RG is a RG. |
| Complement |
They are not closed under complement |
Closed under complement |
| Range |
The range of languages that come under CFG is wide. |
The range of languages that come under RG is less than CFG. |
| Examples |
S –> AB;A –> a;B –> b |
S -> aS | bS | ∊ |
Share your thoughts in the comments
Please Login to comment...