Centre of Mass is the point of anybody where all the mass of the body is concentrated. For the sake of convenience in Newtonian Physics, we take the body as the point object where all its mass is concentrated at the centre of mass of the body. The centre of mass of the body is a point that can be on the body such as in the case of a Circular sheet, rectangle sheet, sphere, etc, and can also be outside the body such as in the case of a ring, hollow sphere, etc.
In this article, we’ll explore the basic fundamentals of the centre of mass, including its definition, methods, and formula to calculate it. We’ll also discuss some real-world examples of the centre of mass to help you see its practical applications. So, let’s start learning about the fascinating world of the centre of mass and its role in the physics of motion.
What is Centre of Mass?
The center of mass (COM) is a theoretical point within an object or system of objects where the entire mass of the object or system can be considered to be concentrated. It is a point that represents the average position of all the mass in the object or system, taking into account both the distribution of mass and its spatial arrangement.
Centre of Mass Definition
The point at which the whole mass of the body seems to be concentrated is called Centre of Mass. It means the point from which we can support the object from below.
For example, a stick can be supported from a middle point such that it does not fall down. Similarly, every object has a similar point which is called the Centre of mass. Its position is defined relative to an object or the system of objects whose Centre of mass is to be calculated. Usually for uniform shapes, it’s their centroid. Let’s start with simple shapes and see where their Centre of masses are located. Consider the shapes given in the figure below. It’s easy to guess the Centre of masses for the following shapes. For most of them, the Centre of mass is at their centroid. The centre of mass of the ring and disc is shown below:

The centre of mass of the rectangle, square and triangular sheet is shown below:

Note: As for a ring, its Centre of mass lies inside the ring, which means it is necessary that the Centre of mass of a body lies in the body itself.
Centre of Mass Formula
Now, it is clear that bodies that are uniform and symmetrical have their Centre of masses at their centroid. But for bodies that are not symmetrical and uniform, the answer is not that simple. The Centre of mass for such bodies can be anywhere. To work out the Centre of mass of a complex object. A weighted average of the locations of each mass of the body is taken.
Let’s say there is a body of mass M, consisting of a set of masses “mi“, each at position ri, then as the total mass seems to concentrate at the centre of mass of the body then:
Mrcm = m1r1 + m2r2 + ….+ mnrn
Thus, the formula for the location of the Centre of mass rcm is given as:
[Tex]\bold{r_{cm} =\frac{ m_1r_1 + m_2r_2 + …+m_nr_n}{M}}
[/Tex]
Where,
- M = ∑mi, which is the total mass of the body.
The above technique uses vector arithmetic. To avoid vector arithmetic, we can find out the Centre of mass of the body along the x-axis and y-axis respectively. Formulas for this case are given below:
[Tex]\bold{x_{cm} = \frac{ m_1x_1 + m_2x_2 + …}{M}}
[/Tex]
[Tex]\bold{y_{cm} = \frac{ m_1y_1 + m_2y_2 + …}{M}}
[/Tex]
Centre of Mass of a Body Having Continuous Mass Distribution
For objects that have non-uniform structures, their centre of mass is calculated by distributing the body into infinitely many small rectangles and then finding the centre of mass of individual rectangles and then integrating them to find the centre of mass of the object.
Suppose the object has mass m and its infinitely small part has mass dm, then the coordinate of its centre of mass is calculated as,
- xcm = ∫(x.dm)/∫dm
- ycm = ∫(y.dm)/∫dm
- zcm = ∫(z.dm)/∫dm
Centre of Mass and Centre of Gravity
Usually, gravity is assumed to be a uniform force acting on the body. In that case, the centre of mass and centre of gravity are almost the same thing but as we change the force of gravity to be non-uniform, then the position of both points changes and we have different centres of mass and centre of gravity for an object in a non-uniform gravitational field.
What is a Rigid Body?
While dealing with the centre of mass we came across various types of bodies that are made up of millions of individual particles. These bodies can change their shape or get deformed if force is applied to them. The bodies which do not get deformed by applying force are called rigid bodies. Thus we can say that rigid bodies are that under stress do not change their shape and their centre of mass remains in the same position.
In the case of any rigid body that has uniform density its centre of mass is generally at its centroid. Some examples of rigid bodies are solid spheres made of steel, solid cylinders, etc.
Centre of Mass for Various Objects
The Centre of Mass for some 3D solids is as follows:
Object | Centre of Mass Location |
|---|
| Sphere | At the centre
|
|---|
| Cube | At the centre
|
|---|
| Cylinder | At the centre
|
|---|
| Cone | One-third of the way up from the base
|
|---|
| Rectangular Prism | At the intersection of the diagonals
|
|---|
| T-Shaped Object | Varies based on the distribution of mass
|
|---|
| L-Shaped Object | Varies based on the distribution of mass
|
|---|
Various Formulas for Centre of Mass
Some systems occur more frequently in real life than others. While calculating the Centre of mass for such systems, the traditional method takes time. Certain centres of mass formulas should be kept in mind while solving the questions related to the Centre of mass. These formulas help in simplifying the calculations.
Center of Mass of System of Two Point Masses
In such a system, COM lies closer to the heavier mass.

m1r1 = m2r2
Distance of COM from mass m1 = [Tex]\frac{m_2r}{m_1 + m_2}
[/Tex]
Distance of COM from mass m2 = [Tex]\frac{m_1r}{m_1 + m_2}
[/Tex]
Centre of Mass of Triangle
The centre of mass of any triangle of height h is at a distance h/3 from its base. If we take a uniform triangle of height h then its centre of mass is at, height h/3 from the base. The image added below shows the same,
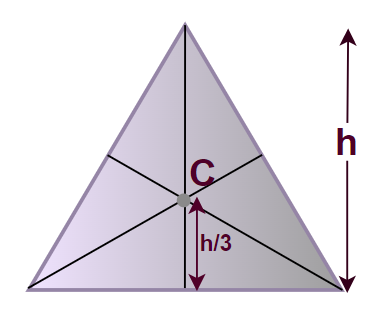
Centre of mass of the triangle lies at the point, which is at the height of h/3
Centre of Mass of Triangle = h/3
where h is the height of the Triangle.
Centre of Mass of Semicircular Disk
The centre of mass of any semi-circular disc of radius r is at a distance of 4r/3π from its base. If we take a uniform semi-circular disc of radius r then its centre of mass is at, height 4r/3π from the base. The image added below shows the same,

Centre of mass of the semi-circular disc lies at the point, which is at the height of 4r/3π
Centre of Mass of Semi-Circular Disc = 4r/3π
where r is the radius of the semi-circular disc
Center of Mass of Half Ring
The centre of mass of any half ring of radius r is at a distance of 2r/π from its base. If we take a uniform semi-circular disc of radius r then its centre of mass is at, height 2r/π from the base. The image added below shows the same,

Centre of mass of the half-ring lies at the point, which is at the height of 2r/π
Centre of Mass of half-ring = 2r/π
where r is the radius of the half-ring.
Centre of Mass of Solid Hemisphere
The centre of mass of a solid hemisphere is located at the intersection of its axis of symmetry and the plane of its circular base. To find the coordinates of the centre of mass of a solid hemisphere of radius R and uniform density, we can use the following formula:
xcm = (3R)/(8π)
The y-coordinate and z-coordinate of the centre of mass are both zero.
Centre of Mass of Solid Cone
The center of mass of a solid cone is located along its axis of symmetry, at a distance of 3/4 times the height of the cone from its base.
To find the coordinates of the centre of mass of a solid cone of radius R, height H, and uniform density, we can use the following formula:
xcm = (3H)/(4π)
The y-coordinate and z-coordinate of the centre of mass are both zero.
Centre of Mass of Hollow Cone
The center of mass of a hollow cone is located along its axis of symmetry, at a distance of 1/4 times the height of the cone from its base.
To find the coordinates of the centre of mass of a hollow cone of radius R, height H, and uniform density, we can use the following formula
xcm = (H/4)(1 + (R/ro)2)
System of Particles
As we have now found the centre of mass of the object that has rigid structures but we also have to find the centre of mass of the objects that are not rigid and are formed by infinite particles that are free to move individually and are not fixed as in case of the uniform body. The particles in this type of body interact with each other through internal forces. In the case of motion of these particles, they move differently for different particles, but there is a point in this body where all the mass of the object can be assumed to be placed and this is called the centre of mass of the body.
Centre of Mass of a System of Particles
The derivation of the Centre of Mass of the System of Particles is explained below:
Suppose we have n particles of masses,
m1, m2, m3, ….., mn. And m1, m2, m3, ….., mn = M
Let their position vector be, [Tex]\vec{r_1},~\vec{r_2},~\vec{r_3},~…..~\vec{r_n}
[/Tex]
Then the centre of mass of this system of particles with respect to the origin is,
[Tex]\vec{r_{cm}}~=~\frac{m_1\vec{r_1}~+~m_2\vec{r_2}~+~m_3\vec{r_3}~+…..~+m_n\vec{r_n}}{m_1~+~m_2~+~m_n~+….+~m_n}
[/Tex]
We know that,
m1, m2, m3, ….., mn = M
[Tex]\vec{r_{cm}}~=~\frac{m_1\vec{r_1}~+~m_2\vec{r_2}~+~m_3\vec{r_3}~+…..~+m_n\vec{r_n}}{m_1~+~m_2~+~m_n~+….+~m_n}
[/Tex]
Two particle system
For two particle system we take two particles of mass m1 and m2 and their position vector be, [Tex]\vec{r_1}~and~\vec{r_2}
[/Tex]
Then the centre of mass of this system of particles with respect to the origin is,
[Tex]\vec{r_{cm}}~=~\frac{m_1\vec{r_1}~+~m_2\vec{r_2}}{m_1~+~m_2}
[/Tex]
In the Cartesian coordinate system,
- Xcm = (m1x1 + m2x2)/(m1 + m2)
- Ycm = (m1y1 + m2y2)/(m1 + m2)
Centre of Mass of the System with Cavity
Suppose we take some part of the body out from the whole body then its centre of mass gets affected. Now the centre of mass of the body is calculated as,
Mass of Body with Cavity = Original Mass of Body(M) + {-Mass of Removed Part(m)}
Suppose the mass of the body is M and the mass of the cavity is m, the centre of mass of the original body is at (x, y, z) and the centre of mass of the cavity is at (x1, y1, z1), then the centre of mass of the object with the cavity is,
- Xcm = (Mx – mx1)/(M – m)
- Ycm = (My – my1)/(M – m)
- Zcm = (Mz – mz1)/(M – m)
Applications of Centre of Mass
The centre of mass has numerous practical applications. Here are some examples:
- Stability: Centre of Mass is taken into consideration while making physical structures in the real world. For example, to make a tall tower or a building its centre of mass needs to be closer to the ground for that building to sustain itself.
- Motion: The motion of an object can be understood with the help of the centre of mass as in many art forms and sports, performer shift their centre of mass to achieve the results.
- Engineering: Engineers use the centre of mass to build structures like buildings and machines like automobiles, that are stable and safe. For example, cranes or bridges are the best examples of machines made by engineers using the centre of mass.
- Astronomy: In the study of the celestial bodies centre of mass play a crucial role.
Read More,
Sample Problems on Center of Mass
Problem 1: Two point masses, m1 = 5Kg and m2 = 2Kg, are located at x = 2 m and x = 6 m respectively. Find the Centre of mass.
Solution:
Formula for the Centre of mass is given by,
[Tex]x_{cm} =\frac{ m_1x_1 + m_2x_2 + …}{M}
[/Tex]
m1 = 5Kg, m2 = 2Kg and x = 2 m and x = 6 m.
M = m1 + m2
⇒ M = 5 + 2 = 7
xcm = [Tex]\frac{ m_1x_1 + m_2x_2 + …}{M}
[/Tex]
⇒ xcm = [Tex]\frac{ m_1x_1 + m_2x_2}{M}
[/Tex]
⇒ xcm = [Tex]\frac{ (5)(2) + (2)(6)}{7}
[/Tex]
⇒ xcm = [Tex]\frac{22}{7}
[/Tex]
Problem 2: Two–point masses, m1 = 5Kg and m2 = 2Kg, are located at y = 10m and y = -5 m respectively. Find the Centre of mass.
Solution:
Formula for the Centre of mass is given by,
[Tex]y_{cm} = \frac{ m_1y_1 + m_2y_2 + …}{M}
[/Tex]
m1 = 5Kg, m2 = 2Kg and y = 10m and y = -5 m.
M = m1 + m2
⇒ M = 5 + 2 = 7
ycm = [Tex]\frac{ m_1y_1 + m_2y_2 + …}{M}
[/Tex]
⇒ ycm = [Tex]\frac{ m_1y_1 + m_2y_2}{M}
[/Tex]
⇒ ycm = [Tex]\frac{ (5)(10) + (2)(-5)}{7}
[/Tex]
⇒ ycm = [Tex]\frac{40}{7}
[/Tex]
Problem 3: Two–point masses, m1 = 1Kg and m2 = 2Kg, are located at vector a = 6i + 4j and vector b = -5i + 2j respectively. Find the Centre of mass.
Solution:
Formula for the Centre of mass in the vector notation is given by,
[Tex]r_{cm} = \frac{ m_1\vec{r_1} + m_2\vec{r_2} + …}{M}
[/Tex]
m1 = 1Kg, m2 = 2Kg and a = 6i + 4j, b = -5i + 2j
M = m1 + m2
⇒ M = 1 + 2 = 3
rcm = [Tex]\frac{ m_1\vec{r_1} + m_2\vec{r_2} + …}{M}
[/Tex]
⇒rcm = [Tex]\frac{ m_1\vec{a} + m_2\vec{b}}{M}
[/Tex]
⇒ rcm = [Tex]\frac{ (1)(6\hat{i} + 4\hat{j} ) + (2)(-5\hat{i} + 2\hat{j})}{7}
[/Tex]
⇒ rcm = [Tex]\frac{ 6\hat{i} + 4\hat{j} + -10\hat{i} + 4\hat{j})}{7}
[/Tex]
⇒ rcm = [Tex]\frac{ -4\hat{i} + 8\hat{j} }{7}
[/Tex]
Problem 4: Two–point masses, m1 = 4Kg and m2 = 2Kg, is located at vector a = i + j and vector b = -i + j respectively. Find the Centre of mass.
Solution:
Formula for the Centre of mass in the vector notation is given by,
[Tex]r_{cm} = \frac{ m_1\vec{r_1} + m_2\vec{r_2} + …}{M}
[/Tex]
m1 = 4Kg, m2 = 2Kg and a = i + j, b = -i + j
M = m1 + m2
⇒ M = 4 + 2 = 6
rcm = [Tex]\frac{ m_1\vec{r_1} + m_2\vec{r_2} + …}{M}
[/Tex]
⇒ rcm = [Tex]\frac{ m_1\vec{a} + m_2\vec{b}}{M}
[/Tex]
⇒ rcm = [Tex]\frac{ (4)(\hat{i} + \hat{j} ) + (2)(\hat{i} -\hat{j})}{7}
[/Tex]
⇒ rcm = [Tex]\frac{ 4\hat{i} + 4\hat{j} + 2\hat{i} -2\hat{j})}{7}
[/Tex]
⇒ rcm = [Tex]\frac{ 6\hat{i} + 2\hat{j} }{7}
[/Tex]
Problem 5: A disk of radius R/2 is removed from a bigger disk of mass M of radius R. Find the Centre of mass.

Solution:
Since the density of the disk is uniform, the weight is uniformly distributed over all the area.
Mass “m” of the removed disk [Tex]= \frac{M (\pi (\frac{R}{2})^2)}{\pi R^2} = \frac{M}{4}
[/Tex]
The figure shows the center of masses of the remaining portion and the removed portion. Notice that if both of these are taken together, the center of mass should lie at the Centre. Let the distance of the center of mass of the remaining portion be “x”.
[Tex]0 = \frac{x\frac{3M}{4} + \frac{R}{2}\frac{M}{4}}{\frac{3M}{4} + \frac{M}{4}} \\ \Rightarrow 0 = x\frac{3M}{4} + \frac{RM}{8} \\ \Rightarrow -\frac{RM}{8} = x\frac{3M}{4} \\ \Rightarrow x = \frac{-R}{6}
[/Tex]
Problem 6: A disk of radius R/4 is removed from a bigger disk of mass M of radius R, in the same manner as the previous figure. Find the Centre of mass.
Solution:
Since the density of the disk is uniform, the weight is uniformly distributed over all the area.
Mass “m” of the removed disk = [Tex]\frac{M (\pi (\frac{R}{4})^2)}{\pi R^2} = \frac{M}{16}
[/Tex]
The figure shows the center of masses of the remaining portion and the removed portion. Notice that if both of these are taken together, the center of mass should lie at the Centre. Let the distance of the center of mass of the remaining portion be “x”.
[Tex]0 = \frac{x\frac{15M}{16} + \frac{R}{2}\frac{M}{16}}{\frac{15M}{16} + \frac{M}{16}} \\ \Rightarrow 0 = x\frac{15M}{16} + \frac{RM}{32} \\ \Rightarrow-\frac{RM}{32} = x\frac{15M}{16} \\ \Rightarrow x = \frac{-R}{30}
[/Tex]
FAQs on Center of Mass
What is centre of mass?
The center of mass is the point in an object or system where the mass seems to be concentrated.
How is centre of mass calculated?
The center of mass is calculated by taking the weighted average of the positions of all the particles in an object or system using mass of each particle as weights.
Can the centre of mass be outside an object?
Yes, the center of mass can lie outside the object. As in the case of a uniform-density ring center of mass is at the center of the inner circle of the ring.
Does the centre of mass change when an object is in motion?
The position of the center of mass may change when an object is in motion if the distribution of mass within the object changes with motion.
What happens when centre of mass is outside an object’s base of support?
When the center of mass is outside an object’s base of support, the object becomes unstable and may tip over or fall. This is why a tall object like a tower must have its center of mass closer to the ground to maintain stability.
Can an object have multiple centres of mass?
No, an object can have only one center of mass. However, a system of objects can have a center of mass that is different from any of the individual objects.
Share your thoughts in the comments
Please Login to comment...