Central Tendencies are the numerical values which are used to represent a large collection of numerical data. These obtained numerical values are called central or average values. A central or average value of any statistical data or series is the value of that variable that is representative of the entire data or its associated frequency distribution.
Some commonly used measures of central tendency are:
Mean Definition
“Mean” in general terms, is referred to the arithmetic mean of a set of data. However, besides the arithmetic mean, there are two other types of means called the geometric mean and the harmonic mean. Each of these means is calculated using different formulas.
Mean for Ungrouped Data
Mean for ungrouped data, also known as the arithmetic mean (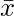 ), is calculated by summing up all individual values in the dataset and dividing the sum by the total number of values. This provides a single representative value that reflects the central tendency of the data. It’s commonly used to understand the average value or typical value of a given set of observations.
), is calculated by summing up all individual values in the dataset and dividing the sum by the total number of values. This provides a single representative value that reflects the central tendency of the data. It’s commonly used to understand the average value or typical value of a given set of observations.
Formula for same is,
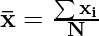
OR
Mean = Sum of all Observations ÷ Total number of Observations
Example: If there are 5 observations, which are 27, 11, 17, 19, and 21 then the mean ( ) is given by
) is given by
 = (27 + 11 + 17 + 19 + 21) ÷ 5
= (27 + 11 + 17 + 19 + 21) ÷ 5
⇒  = 95 ÷ 5
= 95 ÷ 5
⇒ 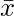 = 19
= 19
Mean for Grouped Data
Mean ( ) is defined for the grouped data as the sum of the product of observations (xi) and their corresponding frequencies (fi) divided by the sum of all the frequencies (fi).
) is defined for the grouped data as the sum of the product of observations (xi) and their corresponding frequencies (fi) divided by the sum of all the frequencies (fi).
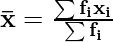
Example: If the values (xi) of the observations and their frequencies (fi) are given as follows:
xi
| 4
| 6
| 15
| 10
| 9
|
|---|
fi
| 5
| 10
| 8
| 7
| 10
|
|---|
then Arithmetic mean (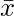 ) of the above distribution is given by
) of the above distribution is given by
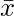 = (4×5 + 6×10 + 15×8 + 10×7 + 9×10) ÷ (5 + 10 + 8 + 7 + 10)
= (4×5 + 6×10 + 15×8 + 10×7 + 9×10) ÷ (5 + 10 + 8 + 7 + 10)
⇒ 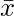 = (20 + 60 + 120 + 70 + 90) ÷ 40
= (20 + 60 + 120 + 70 + 90) ÷ 40
⇒ 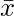 = 360 ÷ 40
= 360 ÷ 40
⇒ 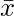 = 9
= 9
Types of Mean
Mean can be classified into three different class groups which are
- Arithmetic Mean
- Geometric Mean
- Harmonic Mean
As Arithmetic mean is already discussed under the heading Mean, Let’s focus on the other two here.
Geometric Mean: The formula for Geometric Mean is given by
![Rendered by QuickLaTeX.com \bold{\text{G.M.} = \sqrt[n]{x_1\cdot x_2\cdot x_3\cdot \ldots \cdot x_n}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1b143a9a5907c1436399abe2f719f385_l3.png)
Where,
- x1, x2, x3, . . ., xn are the observations, and
- n is the number of observations.
Harmonic Mean: The formula for Harmonic Mean is given by
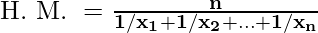
OR
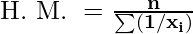
Where,
- x1, x2, . . ., xn are the observations, and
- n is the number of observations.
Properties of Mean (Arithmetic)
There are various properties of Arithmetic Mean, some of which are as follows:
- Algebraic sum of deviations from the arithmetic mean is zero i.e.,
 .
. - If
 is the arithmetic mean of observations and a is added to each of the observations, then the new arithmetic mean is given by
is the arithmetic mean of observations and a is added to each of the observations, then the new arithmetic mean is given by 
- If
 is the arithmetic mean of observations and a is subtracted from each of the observations, then the new arithmetic mean is given by
is the arithmetic mean of observations and a is subtracted from each of the observations, then the new arithmetic mean is given by
- If
 is the arithmetic mean of observations and a is multiplied by each of the observations, then the new arithmetic mean is given by
is the arithmetic mean of observations and a is multiplied by each of the observations, then the new arithmetic mean is given by 
- If
 is the arithmetic mean of observations and each of the observations is divided by a, then the new arithmetic mean is given by
is the arithmetic mean of observations and each of the observations is divided by a, then the new arithmetic mean is given by 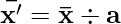 .
.
Median of any distribution is that value that divides the distribution into two equal parts such that the number of observations above it is equal to the number of observations below it. Thus, the median is called the central value of any given data either grouped or ungrouped.
Median of Ungrouped Data
To calculate the Median, the observations must be arranged in ascending or descending order. If the total number of observations is N then there are two cases
Case 1: N is Odd
Median = Value of observation at [(n + 1) ÷ 2]th Position
Case 2: N is Even
Median = Arithmetic mean of Values of observations at (n ÷ 2)th and [(n ÷ 2) + 1]th Position
Example 1: If the observations are 25, 36, 31, 23, 22, 26, 38, 28, 20, 32 then the Median is given by
Arranging data in ascending order: 20, 22, 23, 25, 26, 28, 31, 32, 36, 38
N = 10 which is even then
Median = Arithmetic mean of values at (10 ÷ 2)th and [(10 ÷ 2) + 1]th position
⇒ Median = (Value at 5th position + Value at 6th position) ÷ 2
⇒ Median = (26 + 28) ÷ 2
⇒ Median = 27
Example 2: If the observations are 25, 36, 31, 23, 22, 26, 38, 28, 20 then the Median is given by
Arranging the data in ascending order: 20, 22, 23, 25, 26, 28, 31, 36, 38
N = 9 which is odd then
Median = Value at [(9 + 1) ÷ 2]th position
⇒ Median = Value at 5th position
⇒ Median = 26
Median of Grouped Data
Median of Grouped Data is given as follows:
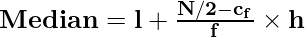
where,
- l is Lower limit of median class
- n is Total number of observations
- cf is Cumulative frequency of the preceding class
- f is Frequency of each class
- h is Class size
Example: Calculate the median for the following data.
Class
| 10 – 20
| 20 – 30
| 30 – 40
| 40 – 50
| 50 – 60
|
|---|
Frequency
| 5
| 10
| 12
| 8
| 5
|
|---|
Solution:
Create the following table for the given data.
| Class | Frequency | Cumulative Frequency |
|---|
10 – 20
| 5
| 5
|
20 – 30
| 10
| 15
|
30 – 40
| 12
| 27
|
40 – 50
| 8
| 35
|
50 – 60
| 5
| 40
|
As n = 40 and n/2 = 20,
Thus, 30 – 40 is the median class.
l = 30, cf = 15, f = 12, and h = 10
Putting the values in the formula \bold{Median =l+ \frac{N/2 – c_f}{f} \times h}
Median = 30 + (20 – 15)/12) × 10
⇒ Median = 30 + (5/12) × 10
⇒ Median = 30 + 4.17
⇒ Median = 34.17
So, median value for this data set is 34.17
Mode
Mode is the value of that observation which has a maximum frequency corresponding to it. In other, that observation of the data occurs the maximum number of times in a dataset.
Mode of Ungrouped Data
Mode of Ungrouped Data can be simply calculated by observing the observation with the highest frequency. Let’s see an example of the calculation of the mode of ungrouped data.
Example: Find the mode of observations 5, 3, 4, 3, 7, 3, 5, 4, 3.
Solution:
Create a table with each observation with its frequency as follows:
Since 3 has occurred a maximum number of times i.e. 4 times in the given data;
Hence, Mode of the given ungrouped data is 3.
Mode of Grouped Data
Formula to find the mode of the grouped data is:
![Rendered by QuickLaTeX.com \bold{Mode = l +\left [\frac{f_1-f_0}{2f_1-f_0-f_2}\right]×h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d280e4acc553b67aa85dc77168fc3e12_l3.png)
where,
- l is the lower class limit of modal class
- h is the class size
- f1 is the frequency of modal class
- f0 is the frequency of class which proceeds the modal class
- f2 is the frequency of class which succeeds the modal class
Example: Find the mode of the dataset which is given as follows.
| Class Interval | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
|---|
| Frequency | 5 | 8 | 12 | 16 | 10 |
|---|
Solution:
As class interval with the highest frequency is 40-50, which has a frequency of 16. Thus, 40-50 is the modal class.
Thus, l = 40 , h = 10 , f1 = 16 , f0 = 12 , f2 = 10
Plugging in the values in formula ![Rendered by QuickLaTeX.com \bold{Mode = l +\left [\frac{f_1-f_0}{2f_1-f_0-f_2}\right]×h}](https://quicklatex.com/cache3/3c/ql_679efc9163c2c89058dbb44af410373c_l3.png) , we get
, we get
Mode = 40 + (16 – 12)/(2 × 16 – 12 – 10) × 10
⇒ Mode = 40 + (4/10)×10
⇒ Mode = 40 + 4
⇒ Mode = 44
Therefore, mode for this set of data is 44.
Empirical Relation Between Measures of Central Tendency
Three central tendencies are related to each other by the empirical formula which is given as follows:
2×Mean + Mode = 3×Median
Formula is used to calculate one of the central tendencies when two other central tendencies are given.
Read More,
FAQs on Central Tendency
What is a Measure of Central Tendency?
Measure of Central Tendency of a dataset represent a central value or a typical value for a dataset which can be used to do further analysis on the data.
What is Mean?
Mean is the Average value of the dataset and can be calculated Arithmetically, Geometrically, and Harmonically as well. Generally by term “mean” means the arithmetic mean of the data.
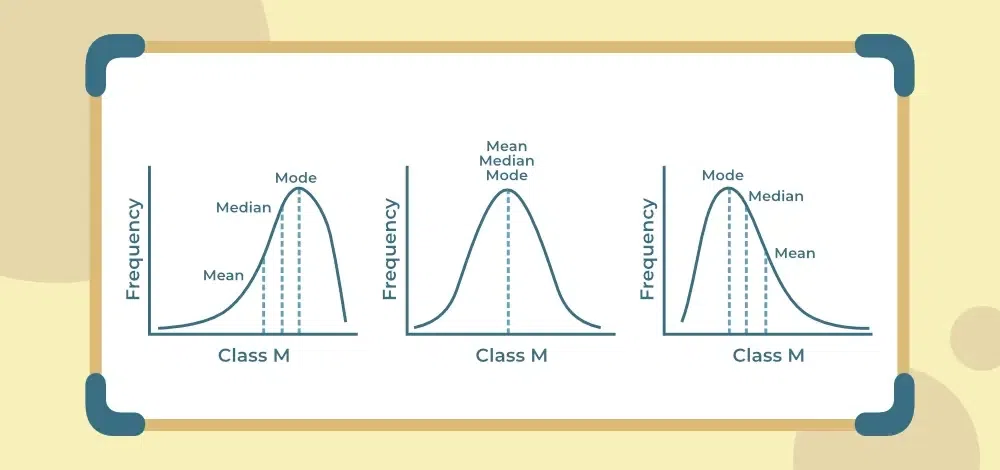
When is Mean a good measure of Central Tendency?
Mean is a good measure of central tendency when data is normally distributed and there is no extreme values or outliers in the dataset.
What is Median?
Median is the middle value of the data set when arranged in increasing or decreasing order i.e., in either ascending or desending order there are equal number of observations on both sides of median.
When is the Median a good measure of Central Tendency?
The median is a good measure of central tendency when dataset is skewed or there are extreme values or outliers in the dataset.
What is Mode?
Mode is highest frequency observation of the given dataset.
When is the Mode a good measure of Central Tendency?
The mode is a good measure of central tendency when there are clear peaks in the dataset of frequencies of observations.
Can a dataset have more than One Mode?
Yes, a dataset can have more than one mode as there can be two observations with same number of highest frequencies.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...