Class 9 RD Sharma Solutions – Chapter 24 Measures of Central Tendency – Exercise 24.3
Last Updated :
18 Mar, 2021
Question 1. Find the median of the following data:
83, 37, 70, 29, 45, 63, 41, 70, 34, 54
Solution:
Ascending order sequence of the numbers :
29, 34, 37, 41, 45, 54, 63, 70, 70, 83
Total number of terms, supposedly, n = 10 (even)
Median =
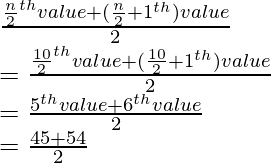
= 99/2
= 49.5
Question 2. Find the median of the following data:
133, 73, 89, 108, 94, 104, 94, 85, 100, 120
Solution:
Ascending order sequence of the numbers :
73, 85, 89, 94, 94, 100, 104, 108, 120, 133
Total number of terms, supposedly, n = 10 (even)
Median =
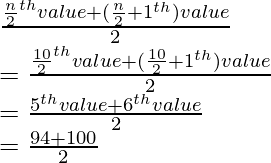
= 194/2
= 97
Question 3. Find the median of the following data:
31, 38, 27, 28, 36, 25, 35, 40
Solution:
Ascending order sequence of the numbers :
25, 27, 28, 31, 35, 36, 38, 40
Total number of terms, supposedly, n = 8 (even)
Median =
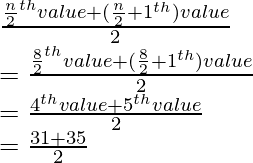
= 66/2
= 33
Question 4. Find the median of the following data:
15, 6, 16, 8, 22, 21, 9, 18, 25
Solution:
Ascending order sequence of the numbers :
6, 8, 9, 15, 16, 18, 21, 22, 25
Total number of terms, supposedly, n = 9 (odd)
Median =
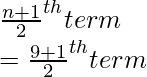
= 5th term
= 16
Question 5. Find the median of the following data:
41, 43, 127, 99, 71, 92, 71, 58, 57
Solution:
Ascending order sequence of the numbers :
41, 43, 57, 58, 71, 71, 92, 99, 127
Total number of terms, supposedly, n = 9 (odd)
Median =
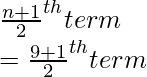
= 5th term
= 71
Question 6. Find the median of the following data:
25, 34, 31, 23, 22, 26, 35, 29, 20, 32
Solution:
Ascending order sequence of the numbers :
20, 22, 23, 25, 26, 29, 31, 32, 34, 35
Total number of terms, supposedly, n = 10 (even)
Median =
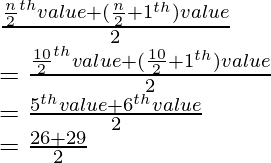
= 55/2
= 27.5
Question 7. Find the median of the following data:
12, 17, 3, 14, 5, 8, 7, 15
Solution:
Ascending order sequence of the numbers :
3, 5, 7, 8, 12, 14, 15, 17
Total number of terms, supposedly, n = 8 (even)
Median =
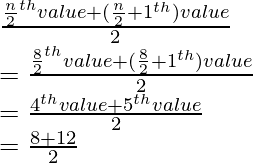
= 20/2
= 10
Question 8. Find the median of the following data:
92, 35, 67, 85, 72, 81, 56, 51, 42, 69
Solution:
Ascending order sequence of the numbers :
35, 42, 51, 56, 67, 69, 72, 81, 85, 92
Total number of terms, supposedly, n = 10 (even)
Median =

= 136/2
= 68
Question 9. Numbers 50, 42, 35, 2x + 10, 2x – 8, 12, 11, 8 are written in descending order and their median is 25, find x.
Solution:
Ascending order sequence of the numbers :
8, 11, 12, 2x – 8, 2x+10, 35, 42, 50
Total number of terms, supposedly, n = 8 (even)
Given,
Median = 25
Median =

48 = 4x
x = 12
Question 10. Find the median of the following observations : 46, 64, 87, 41, 58, 77, 35, 90, 55, 92, 33.If 92 is replaced by 99 and 41 by 43 in the new data, find the new median?
Solution:
Ascending order sequence of the numbers :
33, 35, 41, 46, 55, 58, 64, 77, 87, 90, 92
n = 11 (odd)
Median =
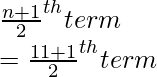
= 6th term
= 58
If we replace 92 by 99 and 41 and 43, then the new sequence of numbers are :
33, 35, 43, 46, 55, 58, 64, 77, 87, 90, 99
New Median =
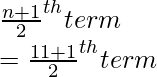
= 6th term
= 58
Question 11. Find the median of the following data : 41, 43, 127, 99, 61, 92, 71, 58, 57. If 58 is replaced by 85, what will be the new median?
Solution:
Arranging the data given in ascending order :
41, 43, 57, 58, 61, 71, 92, 99, 127
Number of terms, supposedly n = 9 (odd)
Median =
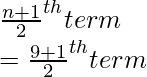
= 5th term
= 61
On replacing the value 58 by 85, we get,
41, 43, 57, 61, 71, 85, 92, 99, 127
New Median =
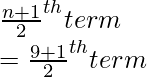
= 5th term
= 71
Question 12. The weights (in kg) of 15 students are : 31, 35, 27, 29, 32, 43, 37, 41, 34, 28, 36, 44, 45, 42,30. Find the median in weight. If the 44 kg is replaced by 446kg and 27 kg by 25kg. Find the new median.
Solution :
Arranging the data in ascending order,
27, 28, 29, 30, 31, 32, 34, 35, 36, 37, 41, 42, 43, 44, 45
Total number of terms = 15 (n = odd)
Median =
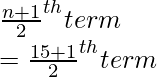
= 8th term
= 35 kg
On replacing 44 kg by 46 kg and 27 kg by 25 kg respectively, we get,
25, 28, 29, 30, 31, 32, 34, 35, 36, 37, 41, 42, 43, 45,46
New Median =
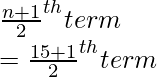
= 8th term
= 35 kg
Question 13. The following observations have been arranged in ascending order. If the median of the data is 63, find the value of x.
29, 32, 48, 50, x, x + 2, 72, 78, 84, 95
Solution :
Given,
Median = 63
Total number of terms, supposedly n = 10 (even)
Now,
Median =

63 = x+1
x = 62
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...