Bayes’s Theorem for Conditional Probability

We strongly recommend to refer below post as a pre-requisite for this.

Bayes’s formula
Below is Bayes’s formula.
$P(A|B) = \frac{P(B|A)P(A)}{P(B)}$

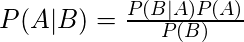
The formula provides the relationship between P(A|B) and P(B|A). It is mainly derived from conditional probability formula discussed in the previous post.
Consider the below formulas for conditional probabilities P(A|B) and P(B|A)
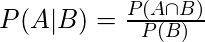
$P(A|B) = \frac{P(A \cap B)}{P(B)}$ —-(1)

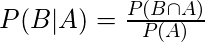
$P(B|A) = \frac{P(B \cap A)}{P(A)}$ —-(2)

Since P(B ∩ A) = P(A ∩ B), we can replace P(A ∩ B) in the first formula with P(B|A)P(A)

After replacing, we get the given formula.

Product Rule

Product rule states that

(1) $\begin{equation*} P(X \cap Y) = P(X|Y)*P(Y) \end{equation*}$

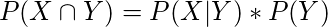
So the joint probability that both X and Y will occur is equal to the product of two terms:

From the product rule :
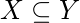
$X \subseteq Y$ implies P(X|Y) = P(X)/P(Y)
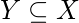
$Y \subseteq X$ implies P(X|Y) = 1

Chain rule

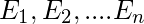
When the above product rule is generalized we lead to chain rule. Let there are $E_{1}, E_{2},....E_{n}$ n events . Then, the joint probability is given by

(2) $\begin{equation*} P(\bigcap_{i=1,..,n}E_{i}) = P(E_{n}|\bigcap_{i=1,..,n-1}E_{i})*P(\bigcap_{i=1,..,n-1}E_{i}) \end{equation*}$

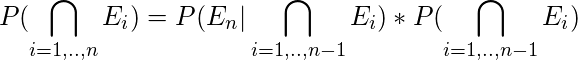
Bayes’ Theorem

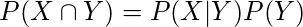
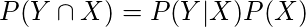
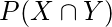
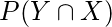
From the product rule, $P(X \cap Y) = P(X|Y)P(Y)$ and $P(Y \cap X) = P(Y|X)P(X)$ . As $P(X \cap Y)$ and $P(Y \cap X)$ are same .

(3) $\begin{equation*} P(Y|X) = \frac{P(X|Y)*P(Y)}{P(X)} \end{equation*}$

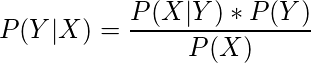
where $P(X) = P(X \cap Y) + P(X \cap Y^{c})$ .

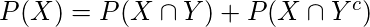
Example : Box P has 2 red balls and 3 blue balls and box Q has 3 red balls and 1 blue ball. A ball is selected as follows:

(i)  Select a box
(ii) Choose a ball from the selected box such that each ball in
     the box is equally likely to be chosen. The probabilities of
     selecting boxes P and Q are (1/3) and (2/3), respectively.

Given that a ball selected in the above process is a red ball, the probability that it came from the box P is (GATE CS 2005)
(A) 4/19
(B) 5/19
(C) 2/9
(D) 19/30

Solution:

R --> Event that red ball is selected
B --> Event that blue ball is selected
P --> Event that box P is selected
Q --> Event that box Q is selected

We need to calculate P(P|R)?


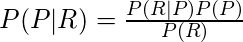P(R|P) = A red ball selected from box P
       = 2/5
P(P) = 1/3
P(R) = P(P)*P(R|P) + P(Q)*P(R|Q)
     = (1/3)*(2/5) + (2/3)*(3/4)
     = 2/15 + 1/2
     = 19/30

Putting above values in the Bayes's Formula
P(P|R) = (2/5)*(1/3) / (19/30)
       = 4/19

Exercise A company buys 70% of its computers from company X and 30% from company Y. Company X produces 1 faulty computer per 5 computers and company Y produces 1 faulty computer per 20 computers. A computer is found faulty what is the probability that it was bought from company X?

Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above

Last Updated : 28 Jun, 2021