Thresholding-Based Image Segmentation
Last Updated :
16 Jan, 2023
Image segmentation is the technique of subdividing an image into constituent sub-regions or distinct objects. The level of detail to which subdivision is carried out depends on the problem being solved. That is, segmentation should stop when the objects or the regions of interest in an application have been detected.
Segmentation of non-trivial images is one of the most difficult tasks in image processing. Segmentation accuracy determines the eventual success or failure of computerized analysis procedures. Segmentation procedures are usually done using two approaches – detecting discontinuity in images and linking edges to form the region (known as edge-based segmenting), and detecting similarity among pixels based on intensity levels (known as threshold-based segmenting).
Mathematically, we can define the problem of segmentation as follows. Let R represent the entire spatial region occupied by an image. Image segmentation tries to divide the region R into sub-regions R1 ,R2 , …. Rn , such that: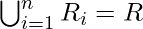
Ri is a connected set for i =1,2,….,n.
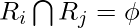 for all i and j.
for all i and j.
Q(Ri) = TRUE for i = 1,2,…,n.
Q(Ri U Rj) = FALSE for any adjacent regions Ri and Rj.
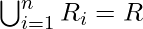
- Ri is a connected set for i =1,2,….,n.
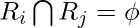 for all i and j.
for all i and j.- Q(Ri) = TRUE for i = 1,2,…,n.
- Q(Ri U Rj) = FALSE for any adjacent regions Ri and Rj.
Here, Q(Ri) is a logical predicate defined over the regions in the set Ri, and \phi represents the null set.
Thresholding
Thresholding is one of the segmentation techniques that generates a binary image (a binary image is one whose pixels have only two values – 0 and 1 and thus requires only one bit to store pixel intensity) from a given grayscale image by separating it into two regions based on a threshold value. Hence pixels having intensity values greater than the said threshold will be treated as white or 1 in the output image and the others will be black or 0.
Suppose the above is the histogram of an image f(x,y). We can see one peak near level 40 and another at 180. So there are two major groups of pixels – one group consisting of pixels having a darker shade and the others having a lighter shade. So there can be an object of interest set in the background. If we use an appropriate threshold value, say 90, will divide the entire image into two distinct regions.
In other words, if we have a threshold T, then the segmented image g(x,y) is computed as shown below:
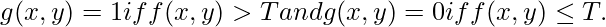
So the output segmented image has only two classes of pixels – one having a value of 1 and others having a value of 0.
If the threshold T is constant in processing over the entire image region, it is said to be global thresholding. If T varies over the image region, we say it is variable thresholding.
Multiple-thresholding classifies the image into three regions – like two distinct objects on a background. The histogram in such cases shows three peaks and two valleys between them. The segmented image can be completed using two appropriate thresholds T1 and T2.
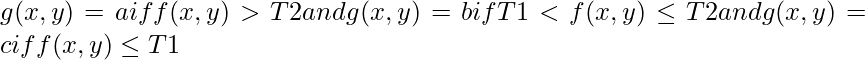
where a, b and c are three distinct intensity values.
From the above discussion, we may intuitively infer that the success of intensity thresholding is directly related to the width and depth of the valleys separating the histogram modes. In turn, the key factors affecting the properties of the valleys are the separation between peaks, the noise content in the image, and the relative sizes of objects and backgrounds. The more widely the two peaks in the histogram are separated, the better thresholding and hence image segmenting algorithms will work. Noise in an image often degrades this widely-separated two-peak histogram distribution and leads to difficulties in adequate thresholding and segmenting. When noise is present, it is appropriate to use some filter to clean the image and then apply segmentation. The relative object sizes play a role in determining the accuracy of segmentation.
Global Thresholding
When the intensity distribution of objects and background are sufficiently distinct, it is possible to use a single or global threshold applicable over the entire image. The basic global thresholding algorithm iteratively finds the best threshold value so segmenting.
The algorithm is explained below.
- Select an initial estimate of the threshold T.
- Segment the image using T to form two groups G1 and G2: G1 consists of all pixels with intensity values > T, and G2 consists of all pixels with intensity values ≤ T.
- Compute the average intensity values m1 and m2 for groups G1 and G2.σ
- Compute the new value of the threshold T as T = (m1 + m2)/2
- Repeat steps 2 through 4 until the difference in the subsequent value of T is smaller than a pre-defined value δ.
- Segment the image as g(x,y) = 1 if f(x,y) > T and g(x,y) = 0 if f(x,y) ≤ T.
This algorithm works well for images that have a clear valley in their histogram. The larger the value of δ, the smaller will be the number of iterations. The initial estimate of T can be made equal to the average pixel intensity of the entire image.
The above simple global thresholding can be made optimum by using Otsu’s method. Otsu’s method is optimum in the sense that it maximizes the between-class variance. The basic idea is that well-thresholded classes or groups should be distinct with respect to the intensity values of their pixels and conversely, a threshold giving the best separation between classes in terms of their intensity values would be the best or optimum threshold.
Variable Thresholding
There are broadly two different approaches to local thresholding. One approach is to partition the image into non-overlapping rectangles. Then the techniques of global thresholding or Otsu’s method are applied to each of the sub-images. Hence in the image partitioning technique, the methods of global thresholding are applied to each sub-image rectangle by assuming that each such rectangle is a separate image in itself. This approach is justified when the sub-image histogram properties are suitable (have two peaks with a wide valley in between) for the application of thresholding techniques but the entire image histogram is corrupted by noise and hence is not ideal for global thresholding.
The other approach is to compute a variable threshold at each point from the neighborhood pixel properties. Let us say that we have a neighborhood Sxy of a pixel having coordinates (x,y). If the mean and standard deviation of pixel intensities in this neighborhood be mxy and σxy , then the threshold at each point can be computed as:
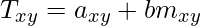
where a and b are arbitrary constants. The above definition of the variable threshold is just an example. Other definitions can also be used according to the need.
The segmented image is computed as:
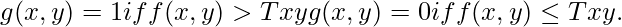
Moving averages can also be used as thresholds. This technique of image thresholding is the most general one and can be applied to widely different cases.
Example 1:
Matlab
image=(imread("coins.jpg"));
figure(1);
imshow(image);
title("Original image.");
[counts,x] = imhist(image,16);
thresh= otsuthresh(counts);
otsu=imbinarize(image,thresh);
figure(2);
imshow(otsu);
title("Image segmentation with Otsu thresholding.");
|
Output:
Share your thoughts in the comments
Please Login to comment...