Thermal Expansion
Last Updated :
31 Aug, 2021
When it comes to liquids, it is observed that when a thermometer is placed in slightly warm water, the mercury in the thermometer rises. When we remove the thermometer from the heated water, the mercury level drops. Similarly, When a balloon is halfway inflated in a cool room and placed in warm water, it will expand to its full size. On the contrary, when a fully inflated balloon is submerged in chilled water, would start shrinking due to the contraction of the air inside.
It has been noted that some sealed bottles with metallic lids are so tightly screwed that the lid must be dipped in hot water for a few minutes to open the lid. This would make the metallic lid expand, and makes the lid easier to unscrew.
Thermal Expansion
Most substances expand when heated and contract when cooled. When a body’s temperature changes, its dimensions change as well. The term “thermal expansion” refers to the expansion of a body’s size as its temperature rises.
There are three types of expansions that can take place in solids,
- Linear expansion
- Area superficial or superficial expansion
- Volume expansion
Linear expansion
Linear expansion refers to the increment in the length of a solid on heating. If the substance is in the form of a long rod, a little variation in temperature, ΔT will cause it to deform, the fractional change in length, Δl/l, is directly proportional to ΔT.
The expression for the linear expansion is,
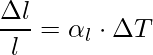
where αl is the coefficient of linear expansion of the given solid.
The unit of α is per degree Celsius (°C-1) in the CGS and per Kelvin (K-1) in the SI system.
The values of coefficient of linear expansion for some material shown in the below table.
| Materials | αl (10–5 K–1) |
|---|
| Aluminum | 2.5 |
| Brass | 1.8 |
| Iron | 1.2 |
| Copper | 1.7 |
| Silver | 1.9 |
| Gold | 1.4 |
| Glass (pyrex) | 0.32 |
| Lead | 0.29 |
Superficial or Area Expansion
Superficial or Area expansion refers to the increment in the surface area of the substance on heating. There is a little variation in temperature, ΔT will cause it to deform, the fractional change in surface area, ΔA/A, is directly proportional to ΔT.
The expression for the Area expansion is,
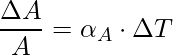
Here, αA is the coefficient of area expansion of the given solid.
Volume expansion
The volume expansion refers to the fractional change in the volume of the substance. There is a little variation in temperature, ΔT will cause it to deform, the fractional change in the volume, ΔV/V, is directly proportional to ΔT.
The expression for the Area expansion is,
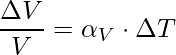
Here αV is also a characteristic of the substance but it does not remain constant, It depends in general on temperature.
The coefficient of volume expansion becomes constant only at a high temperature. For example, Alcohol (ethyl) has a higher coefficient of volume expansion than mercury thus expands more for the same increase in temperature.
The graph plot below shows the Coefficient of volume expansion of copper as a function of temperature.

The Coefficient of volume expansion of copper as a function of temperature.
Anomalous Expansion of Water
The anomalous expansion of water is an abnormal property of water whereby it expands instead of contracting when the temperature goes from 4 °C to 0°C, and it becomes less dense.
- Water has an unusual behavior when heated between 0 and 4 degrees Celsius. As a certain amount of water is cooled from room temperature, its volume drops until the temperature approaches 4 °C.
- The temperature below 4 °C, the volume of water increases, and therefore the density decreases. That means water has a maximum density of 4 °C. This property has a significant impact on a body of water. Lakes and ponds freeze first at the top.
- Water loses energy to the atmosphere, becomes denser, and sinks as a lake cool approaching 4 °C; warmer which is less dense water towards the bottom rises. When the cooler water on top cools to below 4 degrees Celsius, it becomes less dense and settles to the surface, where it freezes.

Thermal expansion of water.
Sample question
Problem 1: Define the term thermal expansion.
Solution:
Most substances expand when heated and contract when cooled. When a body’s temperature changes, its dimensions change as well. The term “thermal expansion” refers to the expansion of a body’s size as its temperature rises.
There are three types of expansions that can take place in solids,
- Linear expansion
- Area superficial or superficial expansion
- Volume expansion
Problem 2: What will be the pressure that has to be applied to the ends of a steel wire of length 10 cm to keep its length constant when its temperature is raised by 100 °C. (For steel Young’s modulus is 2 x 1011 Nm-2 and the coefficient of thermal expansion is 1.1 x 10-5 K-1).
Solution:
Given,
ΔT = 100 °C,
Y = 2 × 1011 N m–2
α = 1.1 × 10–5 K–1
The expression for thermal strain is
ΔF/A=Y(Δl/l)
= YαΔT
Thermal stress in a rod is the pressure due to the thermal strain.
Substitute the value in the above expression.
Thermal strain=(2 × 1011 Nm-2)× (1.1 × 10–5 K-1)×( 100 °C)
= 2.2 × 108 Pa
Problem 3: Two wires are made of the same material and have the same volume. However, wire 1 has cross-sectional area A and wire 2 has cross-sectional area 3A. If the length of wire 1 increases by Dx on applying force F, how much force is needed to stretch wire 2 by the same amount?
Solution:
Young’s modulus is the same for same substance.
The area of the cross-section for the wire 1 is A and wire 2 is 3A.
The volume of wire 1 and 2 is
V1 = V2
(A × l1 )= (3A × l2)
l2 = l1/3
Y = (F/A)/(Δl/l)
or F1 = YA(Δl1/l1)
Similarly,
F2 = Y3A(Δl2/l2)
Wire 2 is stretch by the same amount therefore,
Δl1 = Δl2 = x
F2 = Y3Ax /(l1/3)
F2 = 9(YAx/l1)
F2 = 9F1
Problem 4: Define the term area expansion.
Solution:
Superficial or Area expansion refers to the increment in the surface area of the substance on heating. There is a little variation in temperature, ΔT will cause it to deform, the fractional change in surface area, ΔA/A, is directly proportional to ΔT.
The expression for the Area expansion is
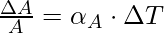
Here, αA is the coefficient of area expansion of the given solid.
Problem 5: Derive the relationship between the coefficient of area expansion (αA) and the coefficient of linear expansion (αl).
Solution:
Consider a cube with a length of l that expands evenly in all directions as its temperature rises by T. The original area will be length square and the new area, after a temperature increase is,
A+ΔA=(l+Δl)2
A+ΔA=l2+(Δl)2+2lΔl
The terms in (Δl)2 have been neglected since Δl is small compared to l.
A+ΔA≈l2+2lΔl
or A+ΔA=A+(2AΔl)/l
or ΔA≈ 2AΔl/l
Rearrange the above equation,
or ΔA/A≈ 2(Δl/l)
or αA=2αl
Therefore, the coefficient of area expansion is twice the coefficient of linear expansion.
Share your thoughts in the comments
Please Login to comment...