When work is done by a force on an object. It acquires energy, it can be any form. Energy can take on many forms and can be converted from one form to another form. Potential energy, electric potential energy, kinetic energy, etc. are some examples of different types of energy. Kinetic energy comes when the object starts moving. This energy is due to motion. Although this energy is due to motion, this energy is not created. It is usually converted from one type of energy to another type. Let’s look at this concept in detail.
Kinetic Energy
If an object is stationary, and we want to put that object into motion. We need to apply force. Any type of acceleration requires some force. When this force is applied, work is done on the object. When the work is done on an object, this means energy is getting transferred to the object is one form or another. Force can be removed once the object is in motion, but till the time force was applied on the object. The work that was done during that time is converted into energy.
Kinetic energy is the energy an object acquires by virtue of its motion.
This energy can be transferred from one object to another. For example, a moving ball hitting a stationary ball might cause the other ball to move. In this situation, some kinetic energy of the ball is transferred to another ball.
Formula of Kinetic Energy
To calculate the kinetic energy of the object, let’s consider a scenario where a force F, is acting on an object of mass M. In this case, the object starts moving with the acceleration “a” and covers a distance of “d”.
Work done in this case will be,
W = F.d
⇒W = m.a.d
The acceleration “a” can be replaced using an equation of motion.
v2 = u2 + 2a.d
⇒v2 – u2 = 2a.d
⇒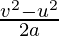 = d
= d
Substituting the value of “d” in the equation,
W = m.a.d
⇒ W = 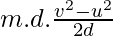
⇒W = 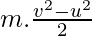
⇒W = 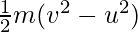
So, this whole work done is converted into the K.E of the object.
In case, initial velocity u = 0,
K.E = 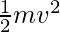
One can also say, the network work done on the system is equal to the change in kinetic energy of the object.
Note:
1. Kinetic energy depends on the velocity of the object squared. This means, when th velocity of the object is doubled, its kinetic energy becomes four times.
2. K.E must always have zero or positive values.
3. Kinetic energy is a scalar quantity, and it is expressed in Joules.
Sample Problems
Question 1: A ball has a mass of 2Kg, suppose it travels at 10m/s. Find the kinetic energy possessed by it.
Answer:
Given: m = 2Kg, and v = 10m/s
The KE is given by,
K.E = 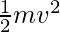
K.E = 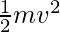
⇒ K.E = 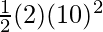
⇒ K.E = 100J
Question 2: A ball has a mass of 10Kg, suppose it travels at 100m/s. Find the kinetic energy possessed by it.
Answer:
Given: m = 10Kg, and v = 100m/s
The KE is given by,
K.E = 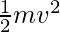
K.E = 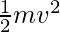
⇒ K.E = 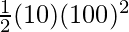
⇒ K.E = 50000J
Question 3: A spaceship has a mass of 20000Kg, suppose it travels at 10m/s. Find the kinetic energy possessed by it.
Answer:
Given: m = 20000Kg, and v = 10m/s
The KE is given by,
K.E = 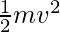
K.E = 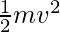
⇒ K.E = 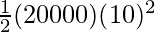
⇒ K.E = 106J
Question 4: Work done by a force on a moving object is 100J. It was traveling at a speed of 2 m/s. Find the new speed of the object if the mass of the object is 2Kg.
Answer:
Given: W = 100J
Work done by the force is equal to the change in kinetic energy.
W = 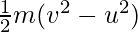
Given, u = 2 m/s and v = ?, m = 2kg.
Plugging the values in the given equation,
W = 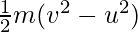
⇒ 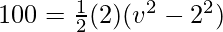
⇒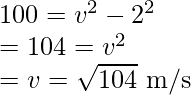
Question 5: Work done by a force on a moving object is -50J. It was traveling at a speed of 10m/s. Find the new speed of the object if the mass of the object is 2Kg.
Answer:
Given: W = -50J
Work done by the force is equal to the change in kinetic energy.
W = 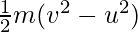
Given, u = 10m/s and v = ? . m = 2kg.
Plugging the values in the given equation,
W = 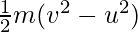
⇒ 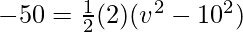
⇒ 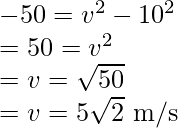
The speed is decreased because the work done was negative. This means that the force was acting opposite to the block and velocity was decreased.
Question 6: Suppose a 1000Kg was traveling at a speed of 10m/s. Now, this mass transfers all its energy to a mass of 10Kg. What will be the velocity of the 10Kg mass after being hit by it?
Answer:
KE is given by the formula,
K.E = 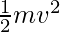
KE of the heavier object
M =1000Kg and v = 10m/s
K.E = 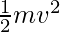
⇒ K.E = 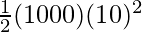
⇒K.E = 50,000J
Now this energy is transferred to another ball.
m = 10Kg and v = ?
50,000 = 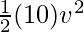
⇒ 10,000 = v2
⇒ v = 100 m/s
Question 7: Suppose a 10Kg was traveling at a speed of 100m/s. Now, this mass transfers all its energy to a mass of 20Kg. What will be the velocity of the 20Kg mass after being hit by it?
Answer:
KE is given by the formula,
K.E = 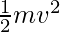
KE of the heavier object
M =10Kg and v = 100m/s
K.E = 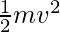
⇒ K.E = 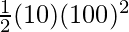
⇒K.E = 50,000J
Now this energy is transferred to another ball.
m = 20Kg and v = ?
50,000 = 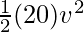
⇒ 5000 = v2
⇒ v = 50√2 m/s
Question 8: Suppose a 10Kg was traveling at a speed of 100m/s. Now, this mass transfers all its energy to a mass of 20Kg. What will be the velocity of the 20Kg mass after being hit by it?
Answer:
KE is given by the formula,
K.E = 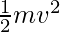
KE of the heavier object
M =10Kg and v = 100m/s
K.E = 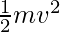
⇒ K.E = 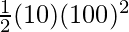
⇒K.E = 50,000J
Now this energy is transferred to another ball.
m = 20Kg and v = ?
50,000 = 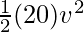
⇒ 5000 = v2
⇒ v = 50√2 m/s
Question 9: Suppose a 10Kg was kept at 20m height. Now, this block is dropped. Find out the velocity of the block just before it hits the ground.
Answer:
The block of 10Kg is kept at a height of 20m.
The potential energy of the block will be,
P.E = mgh
Here m = 10, g = 10m/s2 and h = 20m.
P.E = mgh
⇒ P.E = (10)(10)(20)
⇒ P.E = 2000J
Now, this energy is converted completely into KE.
KE = PE
⇒2000 = 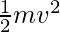
Given m = 10Kg,
⇒2000 = 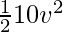
⇒400 = v2
v = 20m/s
Question 10: Suppose a rock of 100Kg was kept at 80m height. Now, this block is dropped. Find out the velocity of the block just before it hits the ground.
Answer:
The block of 10Kg is kept at a height of 20m.
The potential energy of the block will be,
P.E = mgh
Here m = 100, g = 10m/s2 and h = 80m.
P.E = mgh
⇒ P.E = (100)(10)(80)
⇒ P.E = 80000J
Now, this energy is converted completely into KE.
KE = PE
⇒80000 = 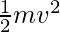
Given m = 100Kg,
⇒80000 = 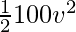
⇒1600 = v2
v = 40m/s
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...