Tabulation vs Memoization
Last Updated :
02 Feb, 2024
Tabulation and memoization are two techniques used in dynamic programming to optimize the execution of a function that has repeated and expensive computations. Although both techniques have similar goals, there are some differences between them.
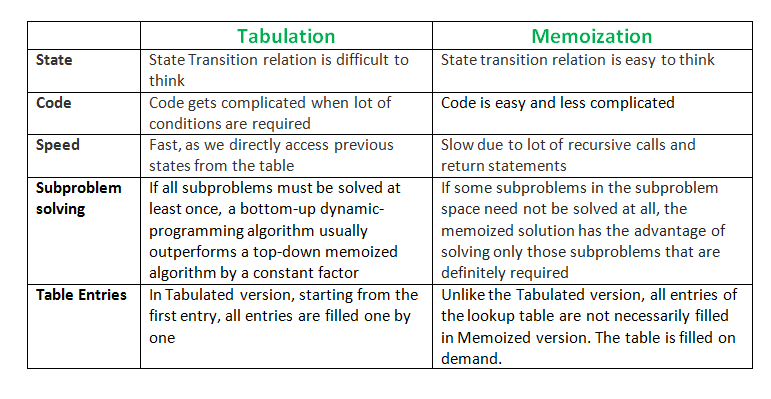
Memoization is a top-down approach where we cache the results of function calls and return the cached result if the function is called again with the same inputs. It is used when we can divide the problem into subproblems and the subproblems have overlapping subproblems. Memoization is typically implemented using recursion and is well-suited for problems that have a relatively small set of inputs.
Tabulation is a bottom-up approach where we store the results of the subproblems in a table and use these results to solve larger subproblems until we solve the entire problem. It is used when we can define the problem as a sequence of subproblems and the subproblems do not overlap. Tabulation is typically implemented using iteration and is well-suited for problems that have a large set of inputs.
Here’s a comparison of memoization and tabulation:
Memoization:
Top-down approach
Caches the results of function calls
Recursive implementation
Well-suited for problems with a relatively small set of inputs
Used when the subproblems have overlapping subproblems
Tabulation:
Bottom-up approach
Stores the results of subproblems in a table
Iterative implementation
Well-suited for problems with a large set of inputs
Used when the subproblems do not overlap
Here’s an example of using memoization and tabulation to solve the same problem – calculating the nth number in the Fibonacci sequence:
Memoization implementation:
C++
#include <iostream>
#include <unordered_map>
int fibonacci(int n, std::unordered_map<int, int>& cache) {
if (cache.find(n) != cache.end()) {
return cache[n];
}
int result;
if (n == 0) {
result = 0;
} else if (n == 1) {
result = 1;
} else {
result = fibonacci(n-1, cache) + fibonacci(n-2, cache);
}
cache[n] = result;
return result;
}
|
Java
import java.util.HashMap;
import java.util.Map;
public class Fibonacci {
public static int fibonacci(int n, Map<Integer, Integer> cache) {
if (cache.containsKey(n)) {
return cache.get(n);
}
int result;
if (n == 0) {
result = 0;
} else if (n == 1) {
result = 1;
} else {
result = fibonacci(n - 1, cache) + fibonacci(n - 2, cache);
}
cache.put(n, result);
return result;
}
public static void main(String[] args) {
int n = 6;
Map<Integer, Integer> cache = new HashMap<>();
int result = fibonacci(n, cache);
System.out.println("The " + n + "th Fibonacci number is: " + result);
}
}
|
Python3
def fibonacci(n, cache={}):
if n in cache:
return cache[n]
if n == 0:
result = 0
elif n == 1:
result = 1
else:
result = fibonacci(n-1) + fibonacci(n-2)
cache[n] = result
return result
|
C#
using System;
using System.Collections.Generic;
class Program
{
static int Fibonacci(int n, Dictionary<int, int> cache)
{
if (cache.ContainsKey(n))
{
return cache[n];
}
int result;
if (n == 0)
{
result = 0;
}
else if (n == 1)
{
result = 1;
}
else
{
result = Fibonacci(n - 1, cache) + Fibonacci(n - 2, cache);
}
cache[n] = result;
return result;
}
static void Main()
{
int n = 10;
Dictionary<int, int> cache = new Dictionary<int, int>();
int result = Fibonacci(n, cache);
Console.WriteLine($"Fibonacci({n}) = {result}");
}
}
|
Javascript
const cache = new Map();
function fibonacci(n) {
if (cache.has(n)) {
return cache.get(n);
}
let result;
if (n === 0) {
result = 0;
} else if (n === 1) {
result = 1;
} else {
result = fibonacci(n - 1) + fibonacci(n - 2);
}
cache.set(n, result);
return result;
}
const n = 10;
const result = fibonacci(n);
console.log(`Fibonacci(${n}) = ${result}`);
|
Tabulation implementation:
C++
#include <iostream>
#include <vector>
int fibonacci(int n)
{
if (n == 0) {
return 0;
}
else if (n == 1) {
return 1;
}
else {
std::vector<int> table(n + 1, 0);
table[0] = 0;
table[1] = 1;
for (int i = 2; i <= n; i++) {
table[i] = table[i - 1] + table[i - 2];
}
return table[n];
}
}
|
Java
import java.util.Arrays;
public class Fibonacci {
public static int fibonacci(int n) {
if (n == 0) {
return 0;
} else if (n == 1) {
return 1;
} else {
int[] table = new int[n + 1];
table[0] = 0;
table[1] = 1;
for (int i = 2; i <= n; i++) {
table[i] = table[i - 1] + table[i - 2];
}
return table[n];
}
}
public static void main(String[] args) {
int n = 6;
int result = fibonacci(n);
System.out.println("The " + n + "th Fibonacci number is: " + result);
}
}
|
Python3
def fibonacci(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
table = [0] * (n + 1)
table[0] = 0
table[1] = 1
for i in range(2, n+1):
table[i] = table[i-1] + table[i-2]
return table[n]
|
C#
using System;
class Fibonacci
{
public static int CalculateFibonacci(int n)
{
if (n == 0)
{
return 0;
}
else if (n == 1)
{
return 1;
}
else
{
int[] table = new int[n + 1];
table[0] = 0;
table[1] = 1;
for (int i = 2; i <= n; i++)
{
table[i] = table[i - 1] + table[i - 2];
}
return table[n];
}
}
static void Main()
{
int n = 6;
int result = CalculateFibonacci(n);
Console.WriteLine($"The {n}th Fibonacci number is: {result}");
}
}
|
Javascript
function fibonacci(n) {
if (n === 0) {
return 0;
} else if (n === 1) {
return 1;
} else {
let table = Array(n + 1).fill(0);
table[0] = 0;
table[1] = 1;
for (let i = 2; i <= n; i++) {
table[i] = table[i - 1] + table[i - 2];
}
return table[n];
}
}
|
In the memoization implementation, we use a dictionary object called cache to store the results of function calls, and we use recursion to compute the results.
In the tabulation implementation, we use an array called table to store the results of subproblems, and we use iteration to compute the results.
Both implementations achieve the same result, but the approach used is different. Memoization is a top-down approach that uses recursion, while tabulation is a bottom-up approach that uses iteration.
Prerequisite – Dynamic Programming, How to solve Dynamic Programming problems?
There are two different ways to store the values so that the values of a sub-problem can be reused. Here, will discuss two patterns of solving dynamic programming (DP) problems:
- Tabulation: Bottom Up
- Memoization: Top Down
Before getting to the definitions of the above two terms consider the following statements:
- Version 1: I will study the theory of DP from GeeksforGeeks, then I will practice some problems on classic DP and hence I will master DP.
- Version 2: To Master DP, I would have to practice Dynamic problems and practice problems – Firstly, I would have to study some theories of DP from GeeksforGeeks
Both versions say the same thing, the difference simply lies in the way of conveying the message and that’s exactly what Bottom-Up and Top-Down DP do. Version 1 can be related to Bottom-Up DP and Version-2 can be related as Top-Down DP.
Tabulation Method – Bottom Up Dynamic Programming
As the name itself suggests starting from the bottom and accumulating answers to the top. Let’s discuss in terms of state transition.
Let’s describe a state for our DP problem to be dp[x] with dp[0] as base state and dp[n] as our destination state. So, we need to find the value of destination state i.e dp[n].
If we start our transition from our base state i.e dp[0] and follow our state transition relation to reach our destination state dp[n], we call it the Bottom-Up approach as it is quite clear that we started our transition from the bottom base state and reached the topmost desired state.
Now, Why do we call it the tabulation method?
To know this let’s first write some code to calculate the factorial of a number using a bottom-up approach. Once, again as our general procedure to solve a DP we first define a state. In this case, we define a state as dp[x], where dp[x] is to find the factorial of x.
Now, it is quite obvious that dp[x+1] = dp[x] * (x+1)
// Tabulated version to find factorial x.
int dp[MAXN];
// base case
int dp[0] = 1;
for (int i = 1; i< =n; i++)
{
dp[i] = dp[i-1] * i;
}
The above code clearly follows the bottom-up approach as it starts its transition from the bottom-most base case dp[0] and reaches its destination state dp[n]. Here, we may notice that the DP table is being populated sequentially and we are directly accessing the calculated states from the table itself and hence, we call it the tabulation method.
Memoization Method – Top-Down Dynamic Programming
Once, again let’s describe it in terms of state transition. If we need to find the value for some state say dp[n] and instead of starting from the base state that i.e dp[0] we ask our answer from the states that can reach the destination state dp[n] following the state transition relation, then it is the top-down fashion of DP.
Here, we start our journey from the top most destination state and compute its answer by taking in count the values of states that can reach the destination state, till we reach the bottom-most base state.
Once again, let’s write the code for the factorial problem in the top-down fashion
// Memoized version to find factorial x.
// To speed up we store the values
// of calculated states
// initialized to -1
int dp[MAXN]
// return fact x!
int solve(int x)
{
if (x==0)
return 1;
if (dp[x]!=-1)
return dp[x];
return (dp[x] = x * solve(x-1));
}
As we can see we are storing the most recent cache up to a limit so that if next time we got a call from the same state we simply return it from the memory. So, this is why we call it memoization as we are storing the most recent state values.
In this case, the memory layout is linear that’s why it may seem that the memory is being filled in a sequential manner like the tabulation method, but you may consider any other top-down DP having 2D memory layout like Min Cost Path, here the memory is not filled in a sequential manner.
This article is contributed by Nitish Kumar.
Share your thoughts in the comments
Please Login to comment...