Python Program for Find largest prime factor of a number
Last Updated :
14 Mar, 2023
Given a positive integer \’n\'( 1 <= n <= 1015). Find the largest prime factor of a number.
Input: 6
Output: 3
Explanation
Prime factor of 6 are- 2, 3
Largest of them is 3
Input: 15
Output: 5
Python3
import math
def maxPrimeFactors (n):
maxPrime = -1
while n % 2 == 0:
maxPrime = 2
n >>= 1
for i in range(3, int(math.sqrt(n)) + 1, 2):
while n % i == 0:
maxPrime = i
n = n / i
if n > 2:
maxPrime = n
return int(maxPrime)
n = 15
print(maxPrimeFactors(n))
n = 25698751364526
print(maxPrimeFactors(n))
|
Time complexity: 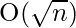
Auxiliary space: 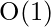
Please refer complete article on Find largest prime factor of a number for more details!
Method 2:
Follow the steps below for the implementation:
- Initialize variables largest_prime to -1, i to 2, and n to the input integer.
- Start a while loop that continues as long as i * i <= n. This loop will iterate through all possible factors of n.
- In the while loop, start another while loop that continues as long as n % i == 0. This inner loop will divide n by i until n is no longer divisible by i.
- In the inner loop, set largest_prime to i, and update n by dividing it by i.
- At the end of the inner loop, increment i by 1.
- After the outer loop, if n > 1, set largest_prime to n. This is because n could be a prime number larger than any of its factors.
- Return largest_prime.
Python3
def largest_prime_factor(n):
largest_prime = -1
i = 2
while i * i <= n:
while n % i == 0:
largest_prime = i
n = n // i
i = i + 1
if n > 1:
largest_prime = n
return largest_prime
n = 15
print(largest_prime_factor(n))
n = 25698751364526
print(largest_prime_factor(n))
|
Time complexity: O(sqrt(n)).
Auxiliary space: O(1),
Share your thoughts in the comments
Please Login to comment...