Kth largest factor of number N

Given two positive integers N and K, the task is to print the Kth largest factor of N.  

Input: N = 12, K = 3
Output: 4
Explanation: The factors of 12 are {1, 2, 3, 4, 6, 12}. The largest factor is 12 and the 3^rd largest factor is 4.

Input: N = 30, K = 2
Output: 15
Explanation: The factors of 30 are {1, 2, 3, 5, 6, 10, 15, 30} and the 2^nd largest factor is 15.

Approach: The idea is to check for each number in the range [N, 1], and print the Kth number that divides N completely.

Iterate through the loop from N to 0. Now, for each number in this loop:

• Check if it divides N or not.
• If N is divisible by the current number, decrement the value of K by 1.
• When K becomes 0, this means that the current number is the Kth largest factor of N.
• Print the answer according to the above observation.

Below is the implementation of the above approach:

C

// C program for the above approach

#include <stdio.h>

// Function to print Kth largest
// factor of N
int KthLargestFactor(int N, int K)
{

    // Check for numbers
    // in the range [N, 1]
    for (int i = N; i > 0; i--) {

        // Check if i is a factor of N
        if (N % i == 0)

            // If Yes, reduce K by 1
            K--;

        // If K is 0, it means
        // i is the required
        // Kth factor of N
        if (K == 0) {
            return i;
        }
    }

    // When K is more
    // than the factors of N
    return -1;
}

// Driver Code
int main()
{
    int N = 12, K = 3;
    printf("%d", KthLargestFactor(N, K));
    return 0;
}

C++

// C++ program for the above approach

#include <iostream>
using namespace std;

// Function to print Kth largest
// factor of N
int KthLargestFactor(int N, int K)
{
    // Check for numbers
    // in the range [N, 1]
    for (int i = N; i > 0; i--) {

        // Check if i is a factor of N
        if (N % i == 0)

            // If Yes, reduce K by 1
            K--;

        // If K is 0, it means
        // i is the required
        // Kth factor of N
        if (K == 0) {
            return i;
        }
    }

    // When K is more
    // than the factors of N
    return -1;
}

// Driver Code
int main()
{
    int N = 12, K = 3;
    cout << KthLargestFactor(N, K);
}

Java

// Java program for the above approach

import java.io.*;

class GFG {

    // Function to print Kth largest
    // factor of N
    static int KthLargestFactor(int N, int K)
    {
        // Check for numbers
        // in the range [N, 1]
        for (int i = N; i > 0; i--) {

            // Check if i is a factor of N
            if (N % i == 0)

                // If Yes, reduce K by 1
                K--;

            // If K is 0, it means
            // i is the required
            // Kth factor of N
            if (K == 0) {
                return i;
            }
        }

        // When K is more
        // than the factors of N
        return -1;
    }

    // Driver Code
    public static void main(String[] args)
    {
        int N = 12, K = 3;
        System.out.println(KthLargestFactor(N, K));
    }
}

Python

# Python program for the above approach

# Function to print Kth largest
# factor of N
def KthLargestFactor(N, K):
    for i in range(N, 0, -1):
        if N % i == 0:
            K -= 1
        if K == 0:
            return i
    return -1


# Driver Code
N = 12
K = 3
print(KthLargestFactor(N, K))

C#

// C# program for the above approach
using System;
using System.Collections.Generic;

class GFG{

// Function to print Kth largest
// factor of N
static int KthLargestFactor(int N, int K)
{

    // Check for numbers
    // in the range [N, 1]
    for (int i = N; i > 0; i--) {

        // Check if i is a factor of N
        if (N % i == 0)

            // If Yes, reduce K by 1
            K--;

        // If K is 0, it means
        // i is the required
        // Kth factor of N
        if (K == 0) {
            return i;
        }
    }

    // When K is more
    // than the factors of N
    return -1;
}

// Driver Code
public static void Main()
{
    int N = 12, K = 3;
    Console.Write(KthLargestFactor(N, K));
}
}

// This code is contributed by ipg2016107.

Javascript

<script>
// JavaScript program for the above approach
// Function to print Kth largest
// factor of N
function KthLargestFactor(N, K)
    {
        // Check for numbers
        // in the range [N, 1]
        for (let i = N; i > 0; i--) {

            // Check if i is a factor of N
            if (N % i == 0)

                // If Yes, reduce K by 1
                K--;

            // If K is 0, it means
            // i is the required
            // Kth factor of N
            if (K == 0) {
                return i;
            }
        }

        // When K is more
        // than the factors of N
        return -1;
    }

// Driver Code
let N = 12, K = 3;
document.write(KthLargestFactor(N, K));

// This code is contributed by shivanisinghss2110
</script>

Output

4

Time Complexity: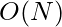 
Auxiliary Space: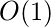 

Efficient Approach: The problem can be solved in an optimized way in sqrt(n) complexity by using the fact that factors of any number remain in the form of pairs. In other words, if i is a factor of number n then n/i  will also be a factor of n. So in order to find all the factors of the number we need to check for factors till sqrt(n) and their corresponding pairs. A similar type of approach is used in the article: find divisors of natural numbers.

Illustration: 
If n = 80, then all the various pairs of divisors possible are: (1,80), (2,40), (4,20), (5,16), (8,10). Hence in order to store all the factors of 80, we will iterate the loop from 1 to √80 ≈ 8 and store the factors in the range(which includes 1,2,4,5,8 here in this case). After this, we run a reverse loop and store the pairs of these previous factors (which will give 10, 16, 20, 40, and 80). Here we are running a reverse loop so that we can get the pairs in increasing order. In this way, we will get all the factors which include {1, 2, 4, 5, 8, 10, 16, 20, 40, and 80}.

Approach:

1. Initialize a vector to store the elements in increasing order.
2. First, iterate a loop from 1 to sqrt(n) and store all the factors.
3. Then iterate the loop in reverse order and for each factor store its corresponding pair. So if i is the factor then store n/i.
4. If the size of the vector is greater or equal to k then return the kth largest factor(which will be v[v.size()-k] as the vector v is in increasing order).
5. If k elements do not exist that means there is no kth largest factor and hence return -1.

Handling the corner cases:
A corner case will arise when any factor is exactly equal to sqrt(n). For example, if n=100, then in this case 10 will be a factor of the number, and also its corresponding pair is 10 as (10*10=100). So in this case 10 will be taken two times. In order to tackle this case, we use an if statement between two loops and remove the issue by considering this factor only one time.

Below is the implementation of the above approach:

C++

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;

// Function to print Kth largest
// factor of N
int KthLargestFactor(int n, int k)
{
    // vector v to store the factors
    // of n in increasing order
    vector<int> v;
    int i;

    // Iterating the loop and checking
    // factors till sqrt(n)
    for (i = 1; i * i <= n; i++) {
        if (n % i == 0)
            v.push_back(i);
    }

    // corner cases
    if (i * i == n) {
        i--;
    }

    for (; i >= 1; i--) {
        if (n % i == 0)
            v.push_back(n / i);
    }

    // When k is less than the factors
    // of n then return the kth
    // largest element which will be
    // will kth element from the end
    // in the vector
    if (k <= v.size()) {
        return v[v.size() - k];
    }

    // When k is more
    // than the factors of n
    else
        return -1;
}

// Driver Code
int main()
{
    int N = 12, K = 3;
    cout << KthLargestFactor(N, K);
}

// This code is contributed by Pushpesh raj

Java

import java.io.*;
import java.util.*;
public class Main
{

  // Function to print Kth largest
  // factor of N
  static int KthLargestFactor(int n, int k)
  {

    // vector v to store the factors
    // of n in increasing order
    ArrayList<Integer> v = new ArrayList<Integer>();
    int i;

    // Iterating the loop and checking
    // factors till sqrt(n)
    for (i = 1; i * i <= n; i++) {
      if (n % i == 0)
        v.add(i);
    }

    // corner cases
    if (i * i == n) {
      i--;
    }

    for (; i >= 1; i--) {
      if (n % i == 0)
        v.add(n / i);
    }

    // When k is less than the factors
    // of n then return the kth
    // largest element which will be
    // will kth element from the end
    // in the vector
    if (k <= v.size()) {
      return v.get(v.size() - k);
    }

    // When k is more
    // than the factors of n
    else
      return -1;
  }

  public static void main(String[] args)
  {
    int N = 12, K = 3;
    System.out.println(KthLargestFactor(N, K));
  }
}

// This code is contributed by garg28harsh.

Python3

# Python program for the above approach
import math

# Function to prKth largest
# factor of N
def KthLargestFactor(n, k):

    # vector v to store the factors
    # of n in increasing order
    v = []

    # Iterating the loop and checking
    # factors till sqrt(n)
    i = 1
    x = math.ceil(math.sqrt(n))
    for j in range (1,x):
        if (n % j == 0):
            v.append(i)
        i = j
    # corner cases
    if (i * i == n):
        i-=1

    # for ( i >= 1 i--) {
    for j in range(i,0,-1):
        if (n % i == 0):
            v.append(math.floor(n / i))

    # When k is less than the factors
    # of n then return the kth
    # largest element which will be
    # will kth element from the end
    # in the vector
    if (k <= len(v)):
        return v[len(v)- k]

    # When k is more
    # than the factors of n
    else:
        return -1

# Driver Code
N = 12
K = 3
print(KthLargestFactor(N, K))

# This code is contributed by akashish__

C#

// C# program for the above approach

using System;
using System.Collections;
using System.Collections.Generic;

public class GFG {

    // Function to print Kth largest
    // factor of N
    static int KthLargestFactor(int n, int k)
    {

        // vector v to store the factors
        // of n in increasing order
        ArrayList v = new ArrayList();
        int i;

        // Iterating the loop and checking
        // factors till sqrt(n)
        for (i = 1; i * i <= n; i++) {
            if (n % i == 0)
                v.Add(i);
        }

        // corner cases
        if (i * i == n) {
            i--;
        }

        for (; i >= 1; i--) {
            if (n % i == 0)
                v.Add(n / i);
        }

        // When k is less than the factors
        // of n then return the kth
        // largest element which will be
        // will kth element from the end
        // in the vector
        if (k <= v.Count) {
            return (int)v[v.Count - k];
        }

        // When k is more
        // than the factors of n
        else
            return -1;
    }

    static public void Main()
    {

        // Code
        int N = 12, K = 3;
        Console.WriteLine(KthLargestFactor(N, K));
    }
}

// This code is contributed by lokeshmvs21.

Javascript

// Javascript program for the above approach

// Function to print Kth largest
// factor of N
function KthLargestFactor(n, k)
{
    // vector v to store the factors
    // of n in increasing order
    var v=[];
    var i;

    // Iterating the loop and checking
    // factors till sqrt(n)
    for (i = 1; i * i <= n; i++) {
        if (n % i == 0)
            v.push(i);
    }

    // corner cases
    if (i * i == n) {
        i--;
    }

    for (; i >= 1; i--) {
        if (n % i == 0)
            v.push(n / i);
    }

    // When k is less than the factors
    // of n then return the kth
    // largest element which will be
    // will kth element from the end
    // in the vector
    if (k <= v.length) {
        return v[v.length - k];
    }

    // When k is more
    // than the factors of n
    else
        return -1;
}

// Driver Code
    var N = 12;
    var K = 3;
    console.log(KthLargestFactor(N, K));

// This code is contributed by Aman Kumar.

Output

4

Time Complexity: O(sqrt(n)) 
Auxiliary Space: O(m) where m is the total number of factors of n.