Python Program for array rotation

Array Rotation:

Image Contributed by SR Dhanush

METHOD 1 (Partitioning the sub arrays and reversing them)

Approach:

Input arr[] = [1, 2, 3, 4, 5, 6, 7, 8], d = 1, size = 8
1) Reverse the entire list by swapping first and last numbers
   i.e start=0, end=size-1
2) Partition the first subarray and reverse the first subarray, by swapping first and last numbers.
   i.e start=0, end=size-d-1
3) Partition the second subarray and reverse the second subarray, by swapping first and last numbers.
   i.e start=size-d, end=size-1

Image Contributed by SR Dhanush

Python3

#Python program to left-rotate the given array

#Function reverse the given array by swapping first and last numbers.
def reverse(start,end,arr):

    #No of iterations needed for reversing the list
    no_of_reverse=end-start+1

    #By incrementing count value swapping of first and last elements is done.
    count=0
    while((no_of_reverse)//2!=count):
        arr[start+count],arr[end-count]=arr[end-count],arr[start+count]
        count+=1
    return arr

#Function takes array, length of array and no of rotations as input
def left_rotate_array(arr,size,d):

    #Reverse the Entire List
    start=0
    end=size-1
    arr=reverse(start,end,arr)

    #Divide array into twosub-array based on no of rotations.
    #Divide First sub-array
    #Reverse the First sub-array
    start=0
    end=size-d-1
    arr=reverse(start,end,arr)

    #Divide Second sub-array
    #Reverse the Second sub-array
    start=size-d
    end=size-1
    arr=reverse(start,end,arr)
    return arr

arr=[1,2,3,4,5,6,7,8]
size=8
d=1
print('Original array:',arr)

#Finding all the symmetric rotation number
if(d<=size):
    print('Rotated array: ',left_rotate_array(arr,size,d))
else:
    d=d%size
    print('Rotated array: ',left_rotate_array(arr,size,d))

#This code contributed by SR.Dhanush

Output

Original array: [1, 2, 3, 4, 5, 6, 7, 8]
Rotated array:  [2, 3, 4, 5, 6, 7, 8, 1]

Time Complexity: O(log10(Half no of elements presents in the given array)). 

Auxiliary Space: O(1).

METHOD 2 (Using temp array):

Write a function rotate(ar[], d, n) that rotates arr[] of size n by d elements. 

Rotation of the above array by 2 will make array

Input arr[] = [1, 2, 3, 4, 5, 6, 7], d = 2, n =7
1) Store d elements in a temp array
   temp[] = [1, 2]
2) Shift rest of the arr[]
   arr[] = [3, 4, 5, 6, 7, 6, 7]
3) Store back the d elements
   arr[] = [3, 4, 5, 6, 7, 1, 2]

Python3

# function to rotate array by d elements using temp array
def rotateArray(arr, n, d):
    temp = []
    i = 0
    while (i < d):
        temp.append(arr[i])
        i = i + 1
    i = 0
    while (d < n):
        arr[i] = arr[d]
        i = i + 1
        d = d + 1
    arr[:] = arr[: i] + temp
    return arr


# Driver function to test above function
arr = [1, 2, 3, 4, 5, 6, 7]
print("Array after left rotation is: ", end=' ')
print(rotateArray(arr, len(arr), 2))

# this code is contributed by Anabhra Tyagi

Output

Array after left rotation is:  [3, 4, 5, 6, 7, 1, 2]

Time complexity: O(n) 
Auxiliary Space: O(d)

METHOD 3 (Rotate one by one) : 

leftRotate(arr[], d, n)
start
  For i = 0 to i < d
    Left rotate all elements of arr[] by one
end

To rotate by one, store arr[0] in a temporary variable temp, move arr[1] to arr[0], arr[2] to arr[1] …and finally temp to arr[n-1]
Let us take the same example arr[] = [1, 2, 3, 4, 5, 6, 7], d = 2 
Rotate arr[] by one 2 times 
We get [2, 3, 4, 5, 6, 7, 1] after first rotation and [ 3, 4, 5, 6, 7, 1, 2] after second rotation. 

Python3

#Function to left rotate arr[] of size n by d*/
def leftRotate(arr, d, n):
    for i in range(d):
        leftRotatebyOne(arr, n)

#Function to left Rotate arr[] of size n by 1*/
def leftRotatebyOne(arr, n):
    temp = arr[0]
    for i in range(n-1):
        arr[i] = arr[i+1]
    arr[n-1] = temp


# utility function to print an array */
def printArray(arr,size):
    for i in range(size):
        print ("%d"% arr[i],end=" ")


# Driver program to test above functions */
arr = [1, 2, 3, 4, 5, 6, 7]
leftRotate(arr, 2, 7)
printArray(arr, 7)

# This code is contributed by Shreyanshi Arun

Output

3 4 5 6 7 1 2 

Time complexity : O(n * d) 
Auxiliary Space : O(1) 

METHOD 4 (A Juggling Algorithm)
This is an extension of method 2. Instead of moving one by one, divide the array in different sets 
where number of sets is equal to GCD of n and d and move the elements within sets. 
If GCD is 1 as is for the above example array (n = 7 and d =2), then elements will be moved within one set only, we just start with temp = arr[0] and keep moving arr[I+d] to arr[I] and finally store temp at the right place.
Here is an example for n =12 and d = 3. GCD is 3 and 

Let arr[] be {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}

a)    Elements are first moved in first set – (See below diagram for this movement

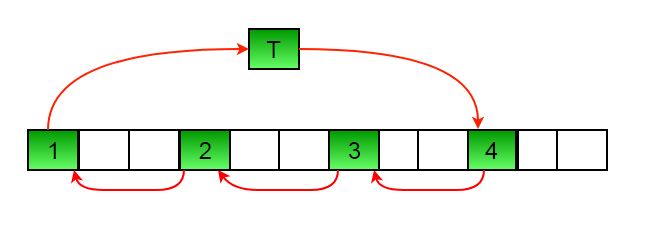
          arr[] after this step --> {4 2 3 7 5 6 10 8 9 1 11 12}

b)    Then in second set.
          arr[] after this step --> {4 5 3 7 8 6 10 11 9 1 2 12}

c)    Finally in third set.
          arr[] after this step --> {4 5 6 7 8 9 10 11 12 1 2 3}

Python3

#Function to left rotate arr[] of size n by d
def leftRotate(arr, d, n):
    for i in range(gcd(d,n)):

        # move i-th values of blocks
        temp = arr[i]
        j = i
        while 1:
            k = j + d
            if k >= n:
                k = k - n
            if k == i:
                break
            arr[j] = arr[k]
            j = k
        arr[j] = temp

#UTILITY FUNCTIONS
#function to print an array
def printArray(arr, size):
    for i in range(size):
        print ("%d" % arr[i], end=" ")

#Function to get gcd of a and b
def gcd(a, b):
    if b == 0:
        return a;
    else:
        return gcd(b, a%b)

# Driver program to test above functions
arr = [1, 2, 3, 4, 5, 6, 7]
leftRotate(arr, 2, 7)
printArray(arr, 7)

# This code is contributed by Shreyanshi Arun

Output

3 4 5 6 7 1 2 

Time complexity : O(n) 
Auxiliary Space : O(1)

Another Approach : Using List slicing

Python3

# Python program using the List
# slicing approach to rotate the array
def rotateList(arr,d,n):
  arr[:]=arr[d:n]+arr[0:d]
  return arr
# Driver function to test above function
arr = [1, 2, 3, 4, 5, 6]
print(arr)
print("Rotated list is")
print(rotateList(arr,2,len(arr)))

# this code is contributed by virusbuddah

Output

[1, 2, 3, 4, 5, 6]
Rotated list is
[3, 4, 5, 6, 1, 2]

If array needs to be rotated by more than its length then mod should be done. 

For example: rotate arr[] of size n by d where d is greater than n. In this case d%n should be calculated and rotate by the result after mod. 

Time complexity : O(n) where n is size of given array
Auxiliary Space : O(1)

Please refer complete article on Program for array rotation for more details!