Puzzle – An Aeroplane Takes a Round-trip in the Wind
Last Updated :
18 Jan, 2023
If an airplane makes a round trip and the wind is blowing, is the trip time shorter, longer, or the same as without wind? Round trip means the airplane goes from point A to point B and then returns to point A.
The velocity of the wind is constant.
.png)
An Aeroplane takes a round trip in wind
Answer:
To begin, meaning roundtrip, we mean that it begins and ends in the same location. Its route is unimportant since it will be subject to a headwind and a tailwind in equal measure. We’ll look at the simple example when the plane flies directly into the wind, spins around, and returns straight back. Alternatively, vice versa.
Let’s look at an example. Assume our plane must fly 300 miles there and 300 miles back. It has a normal cruising speed of 600 miles per hour. In the absence of wind, it will fly 600 miles in exactly one hour. That was easy enough.
If the wind speed is 100 mph, the plane will be wind helped to 700 mph and slowed to 500 mph – Wind Assisted: 300 miles at 700 mph takes 0.429 hours – Wind Slowed: 300 miles at 500 mph takes 0.6 hours – Total Time: 1.029 hours
Let T0 be the time when there is no wind. TW is the wind time. V the unconstrained speed. W is the wind speed, therefore it flies in one direction at V+W and the other at V-W. D denotes the distance there and back.
Let T0 be relatively easily given by:
T0 = D/V
TW is calculated by taking two D/2 trips at speeds V+W and V-W
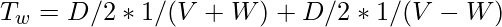
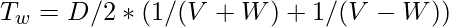
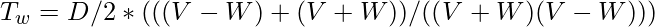
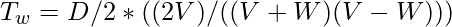
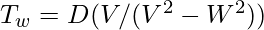
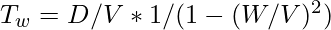
When we show T0 over TW, the reason for such an odd arrangement will become obvious.
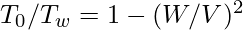
Conclusion:
Here, T0 < TW.
Share your thoughts in the comments
Please Login to comment...