A spring is used in almost every mechanical aspect of our daily lives, from the shock absorbers of a car to a gas lighter in the kitchen. Spring is used because of their property to get deformed and come back to their natural state again. Whenever a spring is stretched or compressed, a force is experienced in the opposite direction of this change. This happens because when a spring deviates from its mean position, it tries to come back there. This force is given by Hooke’s law and helps us to analyze the energy stored in the spring.
Hooke’s law
Force is required to stretch an elastic object such as a metal spring or rope. Whenever an elastic object is stretched or compressed. It tends to exert force to oppose that change in shape. This force is given by Hooke’s law. The force exerted by the spring is called restoring force because it is always in the opposite direction of the deformation.
Hooke’s law states that,
Force required to stretch an elastic object such as a metal spring is directly proportional to the extension of the spring for short distances. Since this restoring force is in the opposite direction, a negative sign is used.
If x is the displacement relative to the unstretched length of the spring and F is the force exerted by it. Then,
F = -kx
Here, k is the spring constant.

So, whenever a spring is stretched downwards, the force is exerted upwards and vice versa.
Elastic Potential Energy
Elastic potential energy is the energy that gets stored in elastic objects when force is applied to them to deform their shape and size. Then energy is stored until the force is removed. After that, objects start to return to their normal shapes and this energy is converted into some other type of energy. Examples of some objects storing elastic potential energy are:
- A stretched or compressed spring.
- A twisted rubber band.
- A bouncy ball, compressed at the moment it strikes the wall and bounces back.
Calculating the potential energy stored in the spring
Hooke’s law mentioned above, states how the restoring force in the spring varies as the net displacement from the mean position of the spring. Considering the net displacement to be 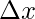 and the restoring force being denoted by F,
and the restoring force being denoted by F,
F = -kx
This force is a conservative force, and conservative forces have potential energies associated with them. It is known that the work done is defined as the product of force and displacement.
W = F.x
For a variable force F, and the net displacement x,
W = 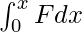
Now at the displacement x, for an infinitesimally small-displacement 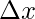 and force F,
and force F,
dW = Fdx
⇒ dW = -kxdx
Integrating the above equation for the total work done,
dW = kxdx
⇒∫dW = ∫kxdx
⇒ W = 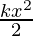
So, this is the total work done for the displacement x. This work done is stored as potential energy in the spring. This fact can also be verified through the force versus displacement graph for the spring. The area under the curve in the force-displacement graph gives the elastic potential energy stored in the spring.

The area under the curve = Area of the shaded region of the curve
= 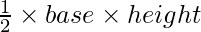
= 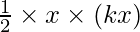
= 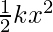
Both of the approaches give the same answer.
Thus, elastic potential energy stored in spring with “x” displacement is given by,
P.E = 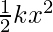
Sample Problems
Question 1: Find the elastic potential energy stored in the spring with k = 50 N/m when the spring is compressed by 0.2m.
Answer:
Given: k = 50 N/m and x = 0.2m
Now, elastic potential energy stored in the spring is given by,
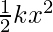
Plugging the values in the above formula,
P.E = 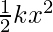
⇒ P.E = 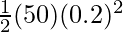
⇒ P.E = 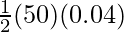
⇒ P.E = 1 J
Question 2: Find the elastic potential energy stored in the spring with k = 100 N/m when the spring is compressed by 0.1m.
Answer:
Given: k = 100 N/m and x = 0.1m
Now, elastic potential energy stored in the spring is given by,
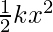
Plugging the values in the above formula,
P.E = 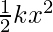
⇒ P.E = 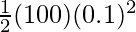
⇒ P.E = 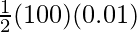
⇒ P.E = 0.5 J
Question 3: Find the elastic potential energy stored in the spring with k = 100 N/m when the spring is stretched to 0.1m from its natural length of 0.5m.
Answer:
Given: k = 100 N/m and xi = 0.1m and xf = 0.5m
Let the displacement x be given by,
x = 0.5 – 0.1
⇒x = 0.4m
Now, elastic potential energy stored in the spring is given by,
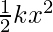
Plugging the values in the above formula,
P.E = 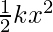
⇒ P.E = 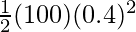
⇒ P.E = 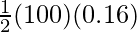
⇒ P.E = 8 J
Question 4: Find the elastic potential energy stored in the spring with k = 100 N/m when the spring is stretched to 0.5m from its natural length of 1 m.
Answer:
Given: k = 100 N/m and xi = 1 m and xf = 0.5m
Let the displacement x be given by,
x = 1 – 0.5
⇒x = 0.5m
Now, elastic potential energy stored in the spring is given by,
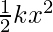
Plugging the values in the above formula,
P.E = 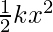
⇒ P.E = 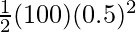
⇒ P.E = 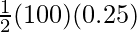
⇒ P.E = 12.5 J
Question 5: A spring with spring constant k = 100 N/m was initially compressed by x = 0.4m, after that, it was released and stopped at x = 0.2m compression. Find the work done by the restoring force in this process.
Answer:
Given: k = 100 N/m and xi = 0.4m and xf = 0.2m
The work done will be given by the difference in potential energy of the spring at these two instances.
Elastic potential energy stored in the spring is given by,
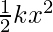
At x = 0.4m
Plugging the values in the above formula,
P.Ei = 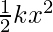
⇒ P.Ei = 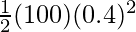
⇒ P.Ei = 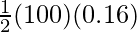
⇒ P.Ei = 8 J
At x = 0.2m
Plugging the values in the above formula,
P.Ef = 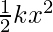
⇒ P.Ef = 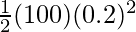
⇒ P.Ef = 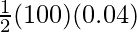
⇒ P.Ef = 2 J
W.D = -(P.Ef – P.Ei)
⇒W.D = -2 + 8
⇒W.D = 6J
Question 6: A spring with spring constant k = 20 N/m was initially compressed by x = 0.5m, after that, it was released and stopped at x = 0.1m compression. Find the work done by the restoring force in this process.
Answer:
Given: k = 20 N/m and xi = 0.5m and xf = 0.1m
The work done will be given by the difference in potential energy of the spring at these two instances.
Elastic potential energy stored in the spring is given by,
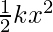
At x = 0.5m
Plugging the values in the above formula,
P.Ei = 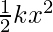
⇒ P.Ei = 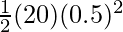
⇒ P.Ei = 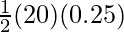
⇒ P.Ei = 2.5 J
At x = 0.1m
Plugging the values in the above formula,
P.Ef = 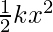
⇒ P.Ef = 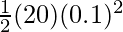
⇒ P.Ef = 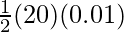
⇒ P.Ef = 0.1 J.
W.D = -(P.Ef – P.Ei)
⇒W.D = -0.1 + 2.5
⇒W.D = 2.4J
Share your thoughts in the comments
Please Login to comment...