Elasticity, this term always reminds of objects like Rubber bands, etc. However, if the question arises, which one is more elastic- A rubber or an Iron piece? The answer will be an Iron piece. Why? The answer lies in the definition of Elasticity, elasticity is known to be the ability of the object to restore its original form after the force is being applied to the object deforming its shape. Let’s learn about elasticity in more detail,
Stress and Strain
When forces are applied to bodies that are elastic in nature, a temporary deformation is caused in them which depends on the nature of the material. This deformation is usually not visible, but it produces a restoring force that tends to bring back the body to its natural state. The magnitude of the restoring force is equal to the force that is applied to the body. Stress has been defined as the restoring force per unit area.
Let F be the magnitude of the force applied on the body and A be the area,
Stress = 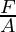
Stress can be classified into three categories. Consider an example to understand how forces act on these stresses:
- Tensile/Compressive Stress: In this kind of stress, the force is perpendicular to the cross-section of the cylinder.
- Shearing Stress: The force is applied parallel to the cross-sectional area of the cylinder.
- Hydraulic Stress: The force is applied to the whole body
Strain is the ratio of change in dimension to the original dimension. For example, in the previous case of a cylinder, different kinds of stress bring about different changes in the dimensions of the cylinder. In the case of compressive or tensile stress, the length of the cylinder is changed.
Let 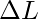 be the change in length of the cylinder and L be the original length. This is called longitudinal strain. It is given by,
be the change in length of the cylinder and L be the original length. This is called longitudinal strain. It is given by,
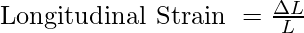
In the case of shearing stress,
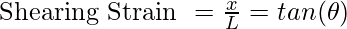
Here,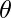 is the angular displacement of the cylinder from its mean position.
is the angular displacement of the cylinder from its mean position.
When hydraulic stress is applied, the body changes its volume. In this case, volumetric strain is used.
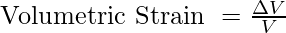
Hooke’s Law
Hooke’s law is based on empirical evidence and is valid for almost all the materials. It helps in establishing a relationship between the stress and the strain in the form of a stress-strain curve. These curves vary from material to material and are very helpful in giving a fair idea of how the material performs in different load conditions. However, this law is only applicable for small displacements. According to Hooke’s law, For small deformations, the stress and the strain produced in the body are directly proportional to each other.”
Stress ∝ Strain
⇒ Stress = k x Strain
Here, k is the proportionality constant and is called the modulus of elasticity.
Elastic Potential Energy
Elastic Potential energy is the energy stored in an object due to its deformation. When a force is applied to an object to deform its shape and size, it does work against a restoring force. In this way, the work done on the object gets stored in the form of the potential energy of the object. This energy is called elastic potential energy. Many times, objects are specifically designed to store the elastic potential energy-
- An ideal spring
- A bouncy ball that compresses when it hits the ground.
- An archer’s stretched bow.
Elastic potential energy stored in the spring
When a spring is compressed with a force F producing the change in length 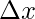 . A restoring force starts acting which tries to bring the body back to an equilibrium position. This force follows Hooke’s law. The work done by this force for the change in length
. A restoring force starts acting which tries to bring the body back to an equilibrium position. This force follows Hooke’s law. The work done by this force for the change in length 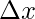 can be calculated either through the methods of integration or by the area under the curve of Hooke’s law.
can be calculated either through the methods of integration or by the area under the curve of Hooke’s law.
Elastic Potential energy stored in the spring = Work done by the force
= 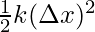
Elastic Potential energy stored in other plastic materials
Spring is an example of an object designed to take advantage of the elastic properties of the material. In the general case of any material, the energy stored due to compression or elongation is calculated through the stress-strain curve. The area under this curve gives us the elastic potential energy stored in the material due to the work done by restoring force.
In the case of three-dimensional materials which obey Hooke’s Law,
Elastic Potential Energy = 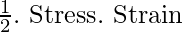
Sample Problems
Question 1: A cube of side 2 m shrinks in size to a length of 0.5 m when hydraulic stress is applied. Find the volumetric strain.
Answer:
Volumetric strain is given by,
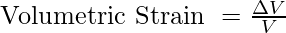
The volume of a cube is given by A
V = a3
Initial radius: ai = 2 m
Final radius: af = 0.5m
Change in Volume = 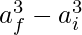
=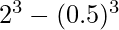
= 7.875
Original Volume = a3
= 1
Volumetric Strain = 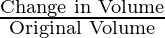
= 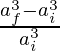
= 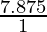
=7.875
Question 2: A sphere of radius 2 m shrinks in size to a radius of 1 m when hydraulic stress is applied. Find the volumetric strain.
Answer:
Volumetric strain is given by,
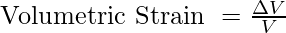
The volume of a sphere is given by A
V = 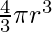
Initial radius: ri = 2 m
Final radius: rf = 1 m
Change in Volume = 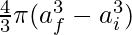
=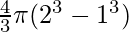
= 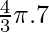
Original Volume = 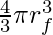
= 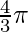
Volumetric Strain = 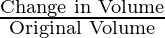
= 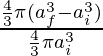
= 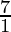
=7
Question 3: A cube of side 1.5m shrinks in size to a length of 0.5 m when the compressive force of 100N is applied. Find the compressive stress.
Answer:
Compressive stress is given by,
Stress = 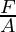
In this case, F = 100N and A = side2.
The side is given as 1.5 m
A = side2.
⇒A = 1.52
⇒A = 2.25
Stress = 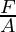
⇒ Stress = 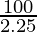
⇒ Stress = 44.44 N/m2
Question 4: A cube of side 3 m shrinks in size to a length of 1 m when the compressive force of 500N is applied. Find the compressive stress.
Answer:
Compressive stress is given by,
Stress = 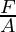
In this case, F = 500N and A = side2.
The side is given as 32m
A = side2.
⇒A = 32
⇒A = 9
Stress = 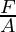
⇒ Stress = 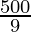
⇒ Stress =55.5 N/m2
Question 5: A spring with k = 50N/m is compressed from its natural length of 1 m to 0.5m. Find the elastic potential energy stored in the spring.
Answer:
The energy stored in the spring is given by,
E.P.E = 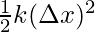
Here, k = 50N/m and 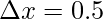
Plugging the values into the given equation,
E.P.E = 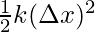
⇒ E.P.E = 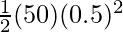
⇒ E.P.E = (25)(0.25)
⇒ E.P.E = 6.25J
Question 6: A spring with k = 100N/m is compressed from its natural length of 2m to 1m. Find the elastic potential energy stored in the spring.
Answer:
The energy stored in the spring is given by,
E.P.E = 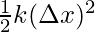
Here, k = 100N/m and 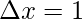
Plugging the values into the given equation,
E.P.E = 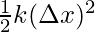
⇒ E.P.E = 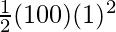
⇒ E.P.E = 50J
Question 7: A spring with k = 50N/m is compressed from its natural length of 1 m to 0.5m. Find the elastic potential energy stored in the spring.
Answer:
The energy stored in the spring is given by,
E.P.E = 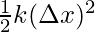
Here, k = 50N/m and 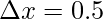
Plugging the values into the given equation,
E.P.E = 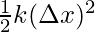
⇒ E.P.E = 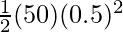
⇒ E.P.E = (25)(0.25)
⇒ E.P.E = 6.25J
Question 8: A spring with k = 100N/m is compressed from its natural length to 0.5m. If the elastic potential energy stored in the spring is 10J, Find the natural length of the spring.
Answer:
The energy stored in the spring is given by,
E.P.E = 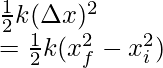
Here, k = 50N/m, xf = 0.5m and xi = ?.
Plugging the values into the given equation,
E.P.E =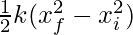
⇒ 10 =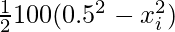
⇒ 20 = 100(0.52 – xi2)
⇒ 0.2 = 0.25 – xi2
⇒xi2= 0.25 – 0.2
⇒xi2= 0.05
⇒xi= √0.05
⇒xi= 0.223
Stress, strain, and elastic potential energy are three related concepts in mechanics and materials science that describe the behavior of materials under stress.
Stress refers to the force per unit area that is applied to a material or structure, and is usually expressed in units of pressure such as pascals (Pa) or pounds per square inch (psi).
Strain refers to the measure of deformation or elongation that occurs in a material or structure due to stress. It is usually expressed as a dimensionless quantity or percentage.
Elastic potential energy refers to the energy stored in a material or structure when it is deformed under stress. When a material is stretched or compressed, it stores elastic potential energy, which can be released when the stress is removed and the material returns to its original shape.
The relationship between stress, strain, and elastic potential energy can be described by Hooke’s law, which states that the amount of deformation or strain in a material is directly proportional to the applied stress, provided the material remains within its elastic limit. In other words, the more stress applied to a material, the more it will deform or stretch, and the more elastic potential energy it will store.
The formula for elastic potential energy can be expressed as:
- Elastic potential energy = 0.5 x stress x strain x volume
- where volume refers to the volume of the material or structure being deformed.
- Understanding the relationship between stress, strain, and elastic potential energy is important in designing and analyzing structures and materials that can withstand different levels of stress and strain without deformation or failure.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...