P-value in Machine Learning
Last Updated :
29 May, 2023
P-value helps us determine how likely it is to get a particular result when the null hypothesis is assumed to be true. It is the probability of getting a sample like ours or more extreme than ours if the null hypothesis is correct. Therefore, if the null hypothesis is assumed to be true, the p-value gives us an estimate of how “strange” our sample is. If the p-value is very small (<0.05 is considered generally), then our sample is “strange,” and this means that our assumption that the null hypothesis is correct is most likely to be false. Thus, we reject it.
What Is P-Value
A P-value is the lowest level (of significance) at which the observed value of the Null Hypothesis statistic is significant. It provides needed evidence for our assumption about the data. Note that the p-value does not provide any probability on our null hypothesis being true or false.
Approach To Hypothesis Testing With P-Value
1. State the null and alternative hypotheses.
2. Choose a fixed significance level α.
3. Choose an appropriate test statistic and establish the critical region based on α.
4. Reject H0 if the computed test statistic is in the critical region.
Otherwise, do not reject.
5. Draw scientific or engineering conclusions.
Examples Of P-Value
1. Average life span of the individual in the US
Let’s take a random sample of 100 records of death in the united states in any certain year and suppose the average life span of these people comes out to be 71.8 years. Here we will assume our data have a standard deviation of 8.9 years. will we be able to conclude that the mean life span today is greater than 70 years? here we will use level of significance value of 0.05(alpha).
Here our null hypothesis (H0) and the alternative hypothesis (H1) are as follows:
H0: μ = 70 years. i.e Mean life span of people is 70 years
H1: μ > 70 years. i.e Mean life span is greater than 70 years\
α = 0.05. level of significance.
Here, x̄ = 71.8 years, σ = 8.9 years,
Since 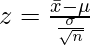
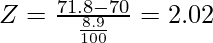
The P -value corresponding to z = 2.02 is given by the area of the shaded region in the following figure.

Distribution graph example
Using the Normal distribution Table we can see that Z provides the area to the left of a given p-value. However, since we want the area to the right of the z-value, we need to subtract the area to the left of the z-value from 1. That is,
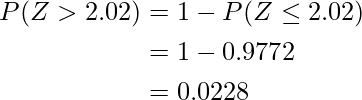
So the p-value corresponding to the z-value of 2.02 is 0.0228 or approximately 0.0217 (rounded to four decimal places). This means that the probability of obtaining a z-value as extreme or more extreme than 2.02 under the null hypothesis is 0.0228 or approximately 0.0217.
As a result, the evidence in favor of H1 is even stronger than that suggested by a 0.05 level of significance. So we Reject H0 and conclude that the mean life span today is greater than 70 years
2. Cookies and Nuts!!
Mary sells chocolate nut cookies. Sadly, there was a complaint that there were fewer peanuts in the chocolate nut cookies than they are supposed to have (a pack of 200g is supposed to have 70g of peanuts). Hence, she wanted to check if the complaint was valid. To do so, she takes 20 random samples of cookies from the population of 400 cookies, unwraps them, and melts the chocolate to weigh the nuts in each packet. If the weights of peanuts in all the 20 samples were much more than 70g and the mean is about 95g, the complaint was definitely not valid. The nut quantity is, in fact, more. Consider that the weights of peanuts in all the 20 samples were much less than 70g, and the mean is about 30g. In this situation, there is a problem with cookies. Here our null hypothesis (H0) and the alternative hypothesis (H1) are as follows:
H0 - Mean weight of peanuts in a packet = 70g (there is no problem with the cookies).
H1 - Mean weight of peanuts in a packet < 70g.
If the weights of peanuts in all the packs are in the range (65,75) which is close to 70g, and the mean is around 68.5g, it is difficult to decide if our claim that H0 is true is correct. In such cases, we find the p-value for this data compared with the mean of 70g. Suppose that the p-value we got is 0.18. Hence, there is an 18% chance of getting a mean as low as this (68.5g) if there is nothing wrong with the cookies (H0 is true) that is the mean weight of peanuts in the cookies >= 70g (Mary is relieved!). If the p-value we obtained were less than the significance level of 0.05, we would reject the null hypothesis.

P-value demonstration
Thus, the p-value tells us if we have evidence from the sample that there is an effect on the population. If the p-value is higher than the significance level, we have no proof. As the p-value goes below the significance level, our evidence gets more potent, and hence we can reject the claim that the null hypothesis is correct.
The procedure we use to find how strong the evidence is as follows –
- Assume that H0 is true.
- Take a sample, get the statistic (mean), and work out how likely it is to get such figures if H0 is true. The parameter which tells us the former is the p-value.
- If the p-value is quite small, H0 is probably wrong. The lower the p-value, the more evidence we have that the null hypothesis is false.
- If the p-value is large, our original idea of assuming H0 to be true is probably correct. Hence, we do not reject H0 – non-significant result.
- P-value is small or large compared to the Significance level, which is generally 0.05. It is adjusted based on the experiment and how we use its results.
Note that, the p-value is not –
- The probability that the claim is valid.
- The probability that the null hypothesis is true.
It is the parameter that helps us determine how “strange” the sample is under the assumption that the null hypothesis is correct. Thereby, it helps us to modify the null hypothesis accordingly.
Share your thoughts in the comments
Please Login to comment...