Optimization in SciPy

SciPy is a Python library that is available for free and open source and is used for technical and scientific computing. It is a set of useful functions and mathematical methods created using Python’s NumPy module.

Features of SciPy:

1. Creating complex programs and specialized applications is a benefit of building SciPy on Python.
2. SciPy contains varieties of sub-packages that help to solve the most common issue related to Scientific Computation.
3. SciPy users benefit from the inclusion of new modules created by programmers all around the world in a variety of software-related fields.
4. Easy to use and understand as well as fast computational power.
5. It can operate on an array of NumPy libraries.

Sub-packages of SciPy:

Packages	Description
scipy.io	File input/output
scipy.special	Special Function(airy, elliptic, bessel, gamma, beta, etc)
scipy.linalg	Linear Algebra Operation
scipy.interpolate	Interpolation
scipy.optimize	Optimization and fit
scipy.stats	Statistics and random numbers
scipy.integrate	Numerical Integration
scipy.fftpack	Fast Fourier transforms
scipy.signal	Signal Processing
scipy.ndimage	Image manipulation

In this article, we will learn the scipy.optimize sub-package.

This package includes functions for minimizing and maximizing objective functions subject to given constraints. Let’s understand this package with the help of examples.

SciPy – Root Finding

func : callable

The function whose root is required. It must be a function of a single variable of the form f(x, a, b, c, . . . ), where a, b, c, . . . are extra arguments that can be passed in the args parameter.

x0 : float, sequence, or ndarray

Initial point from where you want to find the root of the function. It will somewhere near the actual root. Our initial guess is 0.

Find the smallest positive root of the function f(x) = x3 - 2x + 0.5 .

Import the optimize.newton package using the below command. Newton package contains a function that will calculate the root using the Newton Raphson method. Define a function for the given objective function. Use the newton function. This function will return the result object which contains the smallest positive root for the given function f1.

Python3

from scipy.optimize import newton

# objective function

def f1(x):
    return x*x*x - 2*x + 0.5

# newton function will return the root.
print(newton(func2, 0))

Output:

0.25865202250415226

SciPy – Linear Programming 

Maximize: Z = 5x + 4y

Constraints:

• 2y ≤ 50
• x + 2y ≤ 25
• x + y ≤ 15
• x ≥ 0 and y ≥ 0

Import the optimize.linprog module using the following command. Create an array of the objective function’s coefficients. Before that convert the objective function in minimization form by multiplying it with a negative sign in the equation. Now create the two arrays for the constraints equations. One array will be for left-hand equations and the second array for right-hand side values.

Python3

from scipy.optimize import linprog

# Objective function's Coefficient matrix
obj = [-5, -4]

# Constraints Left side x and y Coefficient matrix
lhs_ineq = [[0,  2],   # 0x1 + 2x2
            [1,  2],   # x1 + 2x2
            [1,  1]]  # 1x1 + 1x2

# right side values matrix
rhs_ineq = [50,  # ......<= 50
            25,  # ......<= 25
            15]  # ..... <= 15

 Use the linprog inbuilt function and pass the arrays that we have created an addition mention the method.

Python3

# Inbuilt function <linprog> will
#  solve the problem optimally
# passing the each coefficient's Matrices
opt = linprog(c=obj,
              A_ub=lhs_ineq,
              b_ub=rhs_ineq,
              method="highs")

# printing the solution
print(opt)

Output:

con: array([], dtype=float64)
 crossover_nit: 0
         eqlin:  marginals: array([], dtype=float64)
  residual: array([], dtype=float64)
           fun: -75.0
       ineqlin:  marginals: array([-0., -0., -5.])
  residual: array([50., 10.,  0.])
         lower:  marginals: <MemoryView of 'ndarray' at 0x7f41289de040>
  residual: array([15.,  0.])
       message: 'Optimization terminated successfully.'
           nit: 1
         slack: array([50., 10.,  0.])
        status: 0
       success: True
         upper:  marginals: <MemoryView of 'ndarray' at 0x7f4128a56d40>
  residual: array([inf, inf])
             x: array([15.,  0.])

This function will return an object that contains the optimal answer for the given problem.

SciPy – Assignment Problem 

A city corporation has decided to carry out road repairs on main four arteries of the city. The government has agreed to make a special grant of Rs. 50 lakh towards the cost with a condition that repairs are done at the lowest cost and quickest time. If the conditions warrant, a supplementary token grant will also be considered favourably. The corporation has floated tenders and five contractors have sent in their bids. In order to expedite work, one road will be awarded to only one contractor.

Cost of Repairs ( Rs in lakh)
Contractors	R1	R2	R3	R4	R5
C1	9	14	19	15	13
C2	7	17	20	19	18
C3	8	18	21	18	17
C4	10	12	18	19	18
C5	10	15	21	16	15

Find the best way of assigning the repair work to the contractors and the costs. If it is necessary to seek supplementary grants,what should be the amount sought?

In this code, we required the NumPy array so first install the NumPy module and then import the required modules. Create a multidimensional NumPy array of given data. Use the optimize.linear_sum_assignment() function. This function returns two NumPy arrays (Optimal solution) – one is the row ( Contactors) and the second is the column ( Corresponding Repair Cost). 

Python3

# Import numpy module
import numpy as npy
# Import linear_sum_assignment
from scipy.optimize import linear_sum_assignment


# Cost_Matrix of the given data
cost_matrix = npy.array([[9, 14, 19, 15, 13],
                         [7, 17, 20, 19, 18],
                         [8, 18, 21, 18, 17],
                         [10, 12, 18, 19, 18],
                         [10, 15, 21, 16, 15]])

# Extracting the optimal assignments for
# contractors and corresponding Repair Cost
r, c = linear_sum_assignment(cost_matrix)

Use the sum() function and calculate the total minimum optimal cost.

Python3

# Contactors
print(r)

# Repair costs
print(c)

# Printing the final minimal optimal cost
print(cost_matrix[r, c].sum())

Output:

[0 1 2 3 4]
[4 0 2 1 3]
69

How the assignment will be done can be concluded below from the obtained data.

• Contractor C1 will assign road 1 with a repair cost of 13Rs Lakh. 
• Contractor C2 will assign road 2 with a repair cost of 7RS lakh.
• Contractor C3 will assign road 3 with a repair cost of 21RS lakh.
• Contractor C4 will assign road 4 with a repair cost of 12RS lakh.
• Contractor C5 will assign road 5 with a repair cost of 16RS lakh.

Hence Final Minimal cost  will be,

13 + 7 + 21 + 12 + 16 = Rs. 69 lakh.

SciPy – Minimize 

Broyden-Fletcher-Goldfarb-Shanno ( BFGS )

This algorithm deals with the Minimization of a scalar function of one or more variables. The BFGS algorithm is one of the most widely used second-order algorithms for numerical optimization, and it is frequently used to fit machine learning algorithms such as the logistic regression algorithm.

Objective Function:

• z = sin( X ) + cos( Y )

Python3

# importing the module
import numpy as np
from scipy.optimize import minimize

# BFGS Algorithm -

# define the objective function
def obj(xy):
    x, y = xy
    return np.sin(x)*np.cos(y)

# using the method = 'BFGS'
# and (2,-5) initial point
res = minimize(obj, (2, -5), method='BFGS')

# printing the result
print(res)

Output:

      fun: -0.999999999999904
 hess_inv: array([[ 1.01409071, -0.00302069],
       [-0.00302069,  1.00066793]])
      jac: array([-4.24683094e-07,  9.68575478e-08])
  message: 'Optimization terminated successfully.'
     nfev: 24
      nit: 6
     njev: 8
   status: 0
  success: True
        x: array([ 1.5707959 , -3.14159257])

SciPy – curve_fit

Curve fitting requires that you define the function that maps examples of inputs to outputs like Machine Learning supervised learning. The mapping function can have a straight line (Linear Regression), a Curve line (Polynomial Regression), and much more. A detailed GeeksForGeeks article on Scipy Curve_fit is available here SciPy | Curve Fitting.

Python3

# importing the module
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

# data points -
xd = np.array([-8.0, -7.0, -6.0, -5.0, -4.0, -3.0,
               -2.0, -1.0, 0.0, 1.0, 2.0, 3.0, 4.0,
               5.0, 6.0, 7.0, 8.0])

yd = np.array([13.6, 11.1, 12.0, 14.9, 13.7, 16.1,
               19.6, 17.0, 15.3, 18.4, 14.8, 11.6,
               10.2, 8.9, 9.1, 3.1, 1.1])

# cosine function
def fcos(p, q, r):
    return q*np.cos(r*p)

# Extracting x,y values
# p0 - initial guess
x, y = curve_fit(fcos, xd,
                 yd, p0=[19, 0.1])

print(x, y)

# calling the function
fit_c = fcos(xd, x[0], x[1])

# plotting the graph
plt.plot(xd, yd, 'o', label='data')
plt.plot(xd, fit_c, '-', label='fit')

Output:

[16.45191102  0.14955689] [[1.74663622e+00 1.19187398e-02]
 [1.19187398e-02 2.52349161e-04]]

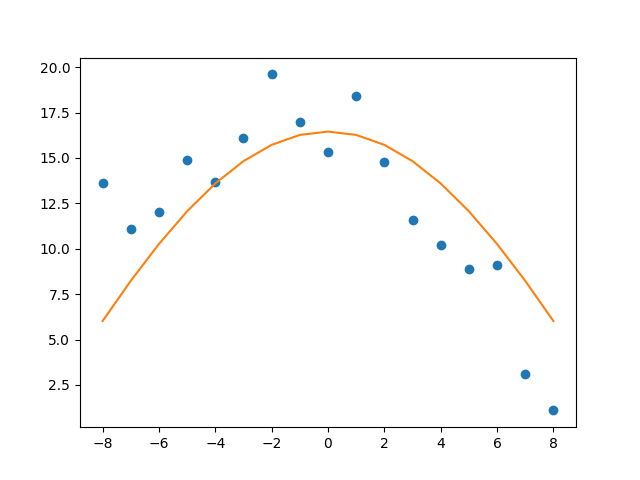
Approximate curve fitted to the input points

SciPy – Univariate Function Minimizers

Non-linear optimization with no constraint and there is only one decision variable in this optimization that we are trying to find a value for.

Python3

# importing the module
from scipy.optimize import minimize_scalar

# Objective function
def A(x):
    return (x - 2) * (x + 2)**2

# printing the optimized result
print(minimize_scalar(A, bounds=(-5, 5), method='bounded'))

Output:

     fun: -9.481481481481376
 message: 'Solution found.'
    nfev: 12
  status: 0
 success: True
       x: 0.6666668296237073

Nelder-Mead Simplex Search  – Machine Learning

Noisy Optimization Problem – A noisy objective function is a function that gives different answers each time the same input is evaluated.

Python3

# nelder-mead optimization of
# noisy one-dimensional convex function
from scipy.optimize import minimize
from numpy.random import randn

# objective function
def A(q):
    return (q + randn(len(q))*0.28)**2.0

# printing the optimal function
print(minimize(A, 0.5, method='nelder-mead'))

Output:

 final_simplex: (array([[0.52539082],
       [0.52539063]]), array([6.79569941e-07, 9.02524100e-05]))
           fun: 6.795699413959474e-07
       message: 'Optimization terminated successfully.'
          nfev: 47
           nit: 18
        status: 0
       success: True
             x: array([0.52539082])