Rules of Inference

Rules of Inference: Every Theorem in Mathematics, or any subject for that matter, is supported by underlying proofs. These proofs are nothing but a set of arguments that are conclusive evidence of the validity of the theory. The arguments are chained together using Rules of Inferences to deduce new statements and ultimately prove that the theorem is valid. 

Definitions

• Argument – A sequence of statements, and premises, that end with a conclusion. 
• Validity – A deductive argument is said to be valid if and only if it takes a form that makes it impossible for the premises to be true and the conclusion nevertheless to be false. 
• Fallacy – An incorrect reasoning or mistake which leads to invalid arguments. 

Table of Rule of inference

Rule of inference	Description
Modus Ponens (MP)	If P implies Q, and P is true, then Q is true.
Modus Tollens (MT)	If P implies Q, and Q is false, then P is false.
Hypothetical Syllogism (HS)	If P implies Q and Q implies R, then P implies R.
Disjunctive Syllogism (DS)	If P or Q is true, and P is false, then Q is true.
Addition (Add)	If P is true, then P or Q is true.
Simplification (Simp)	If P and Q are true, then P is true
Conjunction (Conj)	If P is true and Q is true, then P and Q are true.

Structure of an Argument: As defined, an argument is a sequence of statements called premises that end with a conclusion.

Premises - [Tex]p_{1},\:p_{2},\:p_{3},..., \:p_{n}[/Tex]
Conclusion - [Tex]q[/Tex]

[Tex]if(p_{1}\wedge p_{2}\wedge p_{3}\wedge … \wedge p_{n})\rightarrow q     [/Tex]is a tautology, then the argument is termed valid otherwise termed as invalid. The argument is written as –

[Tex]\begin{tabular}{l}First\:Premise\\Second\:Premise\\Third\:Premise\\.\\.\\Nth\:Premise\\\hline\therefore Conclusion\end{tabular}[/Tex]

Rules of Inference

Simple arguments can be used as building blocks to construct more complicated valid arguments. Certain simple arguments that have been established as valid are very important in terms of their usage. These arguments are called Rules of Inference. The most commonly used Rules of Inference are tabulated below –

[Tex]\begin{tabular}{||c||c||c||}\hlineRule of Inference & Tautology & Name\\\hline\rule{0pt}{8ex} \shortstack[l]{p \\ p\rightarrow q \\ \rule{1cm}{0.5pt}\\ \therefore q}& (p\wedge (p\rightarrow q)) \rightarrow q & Modus Ponens \\\hline\rule{0pt}{8ex} \shortstack[l]{\neg q \\ p\rightarrow q \\ \rule{1cm}{0.5pt}\\ \therefore \neg p}& (\neg q \wedge (p\rightarrow q)) \rightarrow \neg p & Modus Tollens \\\hline\rule{0pt}{8ex} \shortstack[l]{p\rightarrow q \\ q\rightarrow r \\ \rule{1.3cm}{0.5pt}\\ \therefore p \rightarrow r}& ((p\rightarrow q) \wedge (q\rightarrow r)) \rightarrow (p\rightarrow r) & Hypothetical syllogism \\\hline\rule{0pt}{8ex} \shortstack[l]{ \neg p \\ p\vee q \\ \rule{0.8cm}{0.5pt}\\ \therefore q} & (\neg p \wedge (p\vee q)) \rightarrow q & Disjunctive Syllogism \\\hline\rule{0pt}{8ex} \shortstack[l]{p \\ \rule{1.5cm}{0.5pt} \\ \therefore (p \vee q)}& p\rightarrow (p\vee q) & Addition \\\hline\rule{0pt}{8ex} \shortstack[l]{ (p\wedge q)\rightarrow r \\ \rule{2.3cm}{0.5pt}\\ \therefore p\rightarrow (q\rightarrow r)} & ((p\wedge q)\rightarrow r) \rightarrow (p\rightarrow (q\rightarrow r)) & Exportation\\\hline\rule{0pt}{8ex} \shortstack[l]{p\vee q\\\neg p\vee r \\ \rule{1.2cm}{0.5pt} \\ \therefore q\vee r}& ((p\vee q) \wedge(\neg p\vee r)) \rightarrow q\vee r & Resolution \\\hline\end{tabular}[/Tex]

Similarly, we have Rules of Inference for quantified statements –

[Tex]\begin{tabular}{||l||l||}\hlineRule of Inference & Name\\\hline\hline\rule{0pt}{6ex} \shortstack[l]{\forall xP(x) \\ \rule{1cm}{0.5pt}\\ \therefore P(c)} & Universal instantiation \\\hline\rule{0pt}{6ex} \shortstack[l]{P(c) for an arbitrary c\\ \rule{4cm}{0.5pt}\\ \therefore \forall xP(x)} & Universal generalization \\\hline\rule{0pt}{6ex} \shortstack[l]{\exists xP(x)\\ \rule{3cm}{0.5pt} \\ \therefore P(c)\:for\:some\:c} & Existential instantiation \\\hline\rule{0pt}{6ex} \shortstack[l]{P(c) for some c \\ \rule{2.6cm}{0.5pt}\\ \therefore \exists xP(x)} & Existential generalization \\\hline\end{tabular}[/Tex]

Let’s see how Rules of Inference can be used to deduce conclusions from given arguments or check the validity of a given argument.

Example : Show that the hypotheses “It is not sunny this afternoon and it is colder than yesterday”, “We will go swimming only if it is sunny”, “If we do not go swimming, then we will take a canoe trip”, and “If we take a canoe trip, then we will be home by sunset” lead to the conclusion “We will be home by sunset”.

The first step is to identify propositions and use propositional variables to represent them. 

[Tex]p-     [/Tex]“It is sunny this afternoon” [Tex]q-     [/Tex]“It is colder than yesterday” [Tex]r-     [/Tex]“We will go swimming” [Tex]s-     [/Tex]“We will take a canoe trip” [Tex]t-     [/Tex]“We will be home by sunset“

The hypotheses are – [Tex]\neg p \wedge q     [/Tex], [Tex]r\rightarrow p     [/Tex], [Tex]\neg r \rightarrow s     [/Tex], and [Tex]s\rightarrow t     [/Tex]. The conclusion is – [Tex]t     [/Tex]To deduce the conclusion we must use Rules of Inference to construct a proof using the given hypotheses. [Tex]\begin{tabular}{||l||l||} \hline Step & Reason\\ \hline \hline 1. \neg p \wedge q & Hypothesis\\ 2. \neg p & Simplification\\ 3. r \rightarrow p & Hypothesis\\ 4. \neg r & Modus Tollens using (2) and (3)\\ 5. \neg r \rightarrow s & Hypothesis\\ 6. s & Modus Ponens using (4) and (5)\\ 7. s\rightarrow t & Hypothesis\\ 8. t & Modus Ponens Using (6) and (7)\\ \hline \end{tabular}     [/Tex]

Resolution Principle

To understand the Resolution principle, first we need to know certain definitions.

• Literal – A variable or negation of a variable. Eg- [Tex]p, \neg q  [/Tex]
• Sum – Disjunction of literals. Eg- [Tex]p\vee \neg q [/Tex]
• Product – Conjunction of literals. Eg- [Tex]p \wedge \neg q [/Tex]
• Clause – A disjunction of literals i.e. it is a sum.
• Resolvent – For any two clauses [Tex]C_{1}     [/Tex]and [Tex]C_{2}     [/Tex], if there is a literal [Tex]L_{1}     [/Tex]in [Tex]C_{1}     [/Tex]that is complementary to a literal [Tex]L_{2}     [/Tex]in [Tex]C_{2}     [/Tex], then removing both and joining the remaining clauses through a disjunction produces another clause [Tex]C     [/Tex]. [Tex]C     [/Tex]is called the resolvent of [Tex]C_{1}     [/Tex]and [Tex]C_{2} [/Tex]

Rule of inference example

[Tex]C_{1} = p\vee q\vee r[/Tex][Tex]C_{2} = \neg p\vee \neg s \vee t[/Tex]

Here, [Tex]\neg p     [/Tex]and [Tex]p     [/Tex]are complementary to each other. Removing them and joining the remaining clauses with a disjunction gives us- [Tex]q\vee r \vee \neg s\vee t     [/Tex]We could skip the removal part and simply join the clauses to get the same resolvent. [Tex]\since p \vee \neg p \equiv T\: and,\: T \vee q \equiv q     [/Tex]

This is also the Rule of Inference known as Resolution. Theorem – If [Tex]C     [/Tex]is the resolvent of [Tex]C_{1}     [/Tex]and [Tex]C_{2}     [/Tex], then [Tex]C     [/Tex]is also the logical consequence of [Tex]C_{1}     [/Tex]and [Tex]C_{2}     [/Tex]. The Resolution Principle – Given a set [Tex]S     [/Tex]of clauses, a (resolution) deduction of [Tex]C     [/Tex]from [Tex]S     [/Tex]is a finite sequence [Tex]C_{1}, C_{2},…, C_{k}     [/Tex]of clauses such that each [Tex]C_{i}     [/Tex]is either a clause in [Tex]S     [/Tex]or a resolvent of clauses preceding [Tex]C     [/Tex]and [Tex]C_{k} = C     [/Tex]

We can use the resolution principle to check the validity of arguments or deduce conclusions from them. Other Rules of Inference have the same purpose, but Resolution is unique. It is complete by it’s own. You would need no other Rule of Inference to deduce the conclusion from the given argument. To do so, we first need to convert all the premises to clausal form. The next step is to apply the resolution Rule of Inference to them step by step until it cannot be applied any further. For example, consider that we have the following premises –

[Tex]p\rightarrow (q\vee r)[/Tex][Tex]s\rightarrow \neg r[/Tex][Tex]p\wedge s[/Tex]

The first step is to convert them to clausal form –

[Tex]C_{1}: \:\neg p\vee q\vee r[/Tex] [Tex]C_{2}: \:\neg s\vee \neg r[/Tex][Tex]C_{3}: \:p[/Tex][Tex]C_{4}: \:s[/Tex]From the resolution of [Tex]C_{1}[/Tex] and [Tex]C_{2}[/Tex], [Tex]C_{5}:\: \neg p\vee q\vee \neg s[/Tex]From the resolution of [Tex]C_{5}[/Tex] and [Tex]C_{3}[/Tex], [Tex]C_{6}:\: q\vee \neg s[/Tex]From the resolution of [Tex]C_{6}[/Tex] and [Tex]C_{4}[/Tex], [Tex]C_{7}:\: q[/Tex]Therefore, the conclusion is [Tex]q[/Tex].

Note: Implications can also be visualized on octagon as, 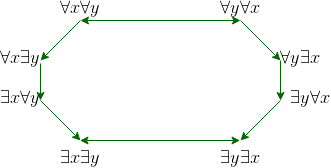It shows how implication changes on changing order of their exists and for all symbols. GATE CS Corner Questions Practicing the following questions will help you test your knowledge. All questions have been asked in GATE in previous years or in GATE Mock Tests.

It is highly recommended that you practice them.

• GATE CS 2004, Question 70
• GATE CS 2015 Set-2, Question 13

References-

• Rules of Inference
• Simon Fraser University Rules of Inference
• Wikipedia Fallacy
• Wikipedia Book
• Discrete Mathematics and
• Its Applications by Kenneth Rosen

Conclusion – Rules of inference

In logic, each rule of inference leads to a specific conclusion based on given premises. Modus Ponens establishes that if a statement P implies Q, and P is true, then Q must also be true. Conversely, Modus Tollens asserts that if P implies Q, and Q is false, then P must be false. Hypothetical Syllogism extends this reasoning by stating that if P implies Q and Q implies R, then P implies R. Disjunctive Syllogism states that if either P or Q is true, and P is false, then Q must be true. Addition indicates that if P is true, then P or Q is true. Simplification dictates that if both P and Q are true, then P must be true. Finally, Conjunction states that if both P and Q are true, then both P and Q are true. These rules collectively provide a framework for making logical deductions from given statements.

Rule of inference – FAQs

What are the rules of inference explain with examples?

The rule of inference known as modus ponens. It involves two statements: one in the format “If p, then q” and another simply stating “p”. When these premises are combined, the conclusion drawn is “q”.

What are the 8 valid rules of inference?

They also cover eight valid forms of inference: modus ponens, modus tollens, hypothetical syllogism, simplification, conjunction, disjunctive syllogism, addition, and constructive dilemma

What is an example of the rules of inference resolution?

If it snows, I’ll study discrete math. If I study discrete math, I’ll get an A. Therefore, if it snows, I’ll get an A.

An example rule of inference: modus ponens?

• If it is raining (P), then the ground is wet (Q).
• It is indeed raining (P).
• Therefore, we can infer that the ground is wet (Q).

This logical process is known as modus ponens.

What are the 7 rules of inference?

The seven commonly used rules of inference in logic are:

Modus Ponens (MP)

Modus Tollens (MT)

Hypothetical Syllogism (HS)

Disjunctive Syllogism (DS)

Addition (Add)

Simplification (Simp)

Conjunction (Conj)

If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.