What is Dijkstra’s Algorithm? | Introduction to Dijkstra’s Shortest Path Algorithm
Last Updated :
08 Mar, 2024
In this article, we will be discussing one of the most commonly known shortest-path algorithms i.e. Dijkstra’s Shortest Path Algorithm which was developed by Dutch computer scientist Edsger W. Dijkstra in 1956. Moreover, we will do a complexity analysis for this algorithm and also see how it differs from other shortest-path algorithms.
.jpg)
Dijkstra’s Algorithm:
Dijkstra’s algorithm is a popular algorithms for solving many single-source shortest path problems having non-negative edge weight in the graphs i.e., it is to find the shortest distance between two vertices on a graph. It was conceived by Dutch computer scientist Edsger W. Dijkstra in 1956.
The algorithm maintains a set of visited vertices and a set of unvisited vertices. It starts at the source vertex and iteratively selects the unvisited vertex with the smallest tentative distance from the source. It then visits the neighbors of this vertex and updates their tentative distances if a shorter path is found. This process continues until the destination vertex is reached, or all reachable vertices have been visited.
Need for Dijkstra’s Algorithm (Purpose and Use-Cases)
The need for Dijkstra’s algorithm arises in many applications where finding the shortest path between two points is crucial.
For example, It can be used in the routing protocols for computer networks and also used by map systems to find the shortest path between starting point and the Destination (as explained in How does Google Maps work?)
Can Dijkstra’s Algorithm work on both Directed and Undirected graphs?
Yes, Dijkstra’s algorithm can work on both directed graphs and undirected graphs as this algorithm is designed to work on any type of graph as long as it meets the requirements of having non-negative edge weights and being connected.
- In a directed graph, each edge has a direction, indicating the direction of travel between the vertices connected by the edge. In this case, the algorithm follows the direction of the edges when searching for the shortest path.
- In an undirected graph, the edges have no direction, and the algorithm can traverse both forward and backward along the edges when searching for the shortest path.
Algorithm for Dijkstra’s Algorithm:
- Mark the source node with a current distance of 0 and the rest with infinity.
- Set the non-visited node with the smallest current distance as the current node.
- For each neighbor, N of the current node adds the current distance of the adjacent node with the weight of the edge connecting 0->1. If it is smaller than the current distance of Node, set it as the new current distance of N.
- Mark the current node 1 as visited.
- Go to step 2 if there are any nodes are unvisited.
How does Dijkstra’s Algorithm works?
Let’s see how Dijkstra’s Algorithm works with an example given below:
Dijkstra’s Algorithm will generate the shortest path from Node 0 to all other Nodes in the graph.
Consider the below graph:
.png)
Dijkstra’s Algorithm
The algorithm will generate the shortest path from node 0 to all the other nodes in the graph.
For this graph, we will assume that the weight of the edges represents the distance between two nodes.
As, we can see we have the shortest path from,
Node 0 to Node 1, from
Node 0 to Node 2, from
Node 0 to Node 3, from
Node 0 to Node 4, from
Node 0 to Node 6.
Initially we have a set of resources given below :
- The Distance from the source node to itself is 0. In this example the source node is 0.
- The distance from the source node to all other node is unknown so we mark all of them as infinity.
Example: 0 -> 0, 1-> ∞,2-> ∞,3-> ∞,4-> ∞,5-> ∞,6-> ∞.
- we’ll also have an array of unvisited elements that will keep track of unvisited or unmarked Nodes.
- Algorithm will complete when all the nodes marked as visited and the distance between them added to the path. Unvisited Nodes:- 0 1 2 3 4 5 6.
Step 1: Start from Node 0 and mark Node as visited as you can check in below image visited Node is marked red.
.png)
Dijkstra’s Algorithm
Step 2: Check for adjacent Nodes, Now we have to choices (Either choose Node1 with distance 2 or either choose Node 2 with distance 6 ) and choose Node with minimum distance. In this step Node 1 is Minimum distance adjacent Node, so marked it as visited and add up the distance.
Distance: Node 0 -> Node 1 = 2
.png)
Dijkstra’s Algorithm
Step 3: Then Move Forward and check for adjacent Node which is Node 3, so marked it as visited and add up the distance, Now the distance will be:
Distance: Node 0 -> Node 1 -> Node 3 = 2 + 5 = 7
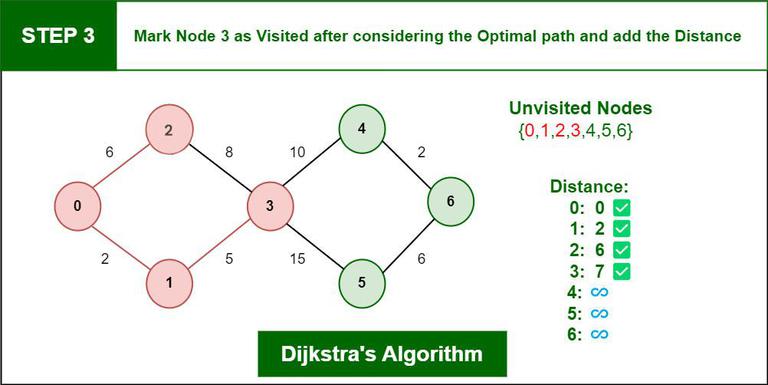
Dijkstra’s Algorithm
Step 4: Again we have two choices for adjacent Nodes (Either we can choose Node 4 with distance 10 or either we can choose Node 5 with distance 15) so choose Node with minimum distance. In this step Node 4 is Minimum distance adjacent Node, so marked it as visited and add up the distance.
Distance: Node 0 -> Node 1 -> Node 3 -> Node 4 = 2 + 5 + 10 = 17
.png)
Dijkstra’s Algorithm
Step 5: Again, Move Forward and check for adjacent Node which is Node 6, so marked it as visited and add up the distance, Now the distance will be:
Distance: Node 0 -> Node 1 -> Node 3 -> Node 4 -> Node 6 = 2 + 5 + 10 + 2 = 19
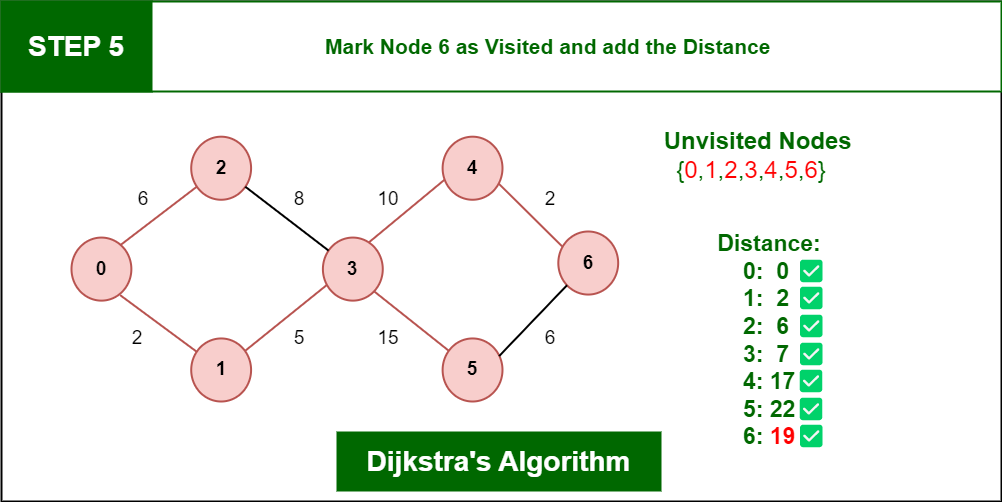
Dijkstra’s Algorithm
So, the Shortest Distance from the Source Vertex is 19 which is optimal one
Pseudo Code for Dijkstra’s Algorithm
function Dijkstra(Graph, source):
// Initialize distances to all nodes as infinity, except for the source node.
distances = map infinity to all nodes
distances = 0
// Initialize an empty set of visited nodes and a priority queue to keep track of the nodes to visit.
visited = empty set
queue = new PriorityQueue()
queue.enqueue(source, 0)
// Loop until all nodes have been visited.
while queue is not empty:
// Dequeue the node with the smallest distance from the priority queue.
current = queue.dequeue()
// If the node has already been visited, skip it.
if current in visited:
continue
// Mark the node as visited.
visited.add(current)
// Check all neighboring nodes to see if their distances need to be updated.
for neighbor in Graph.neighbors(current):
// Calculate the tentative distance to the neighbor through the current node.
tentative_distance = distances[current] + Graph.distance(current, neighbor)
// If the tentative distance is smaller than the current distance to the neighbor, update the distance.
if tentative_distance < distances[neighbor]:
distances[neighbor] = tentative_distance
// Enqueue the neighbor with its new distance to be considered for visitation in the future.
queue.enqueue(neighbor, distances[neighbor])
// Return the calculated distances from the source to all other nodes in the graph.
return distances
Implemention of Dijkstra’s Algorithm:
There are several ways to Implement Dijkstra’s algorithm, but the most common ones are:
- Priority Queue (Heap-based Implementation):
- Array-based Implementation:
In this Implementation, we are given a graph and a source vertex in the graph, finding the shortest paths from the source to all vertices in the given graph.
Example:
Input: Source = 0
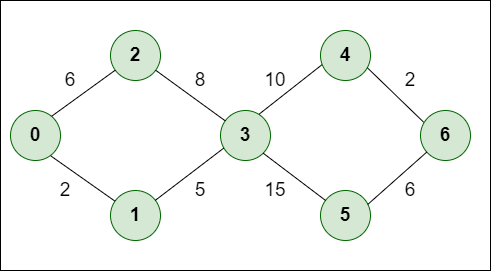
Example
Output: Vertex
Vertex Distance from Source
0 -> 0
1 -> 2
2 -> 6
3 -> 7
4 -> 17
5 -> 22
6 -> 19
Below is the algorithm based on the above idea:
- Initialize the distance values and priority queue.
- Insert the source node into the priority queue with distance 0.
- While the priority queue is not empty:
- Extract the node with the minimum distance from the priority queue.
- Update the distances of its neighbors if a shorter path is found.
- Insert updated neighbors into the priority queue.
Below is the C++ Implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
typedef pair<int, int> iPair;
class Graph {
int V;
list<pair<int, int> >* adj;
public:
Graph(int V);
void addEdge(int u, int v, int w);
void shortestPath(int s);
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<iPair>[V];
}
void Graph::addEdge(int u, int v, int w)
{
adj[u].push_back(make_pair(v, w));
adj[v].push_back(make_pair(u, w));
}
void Graph::shortestPath(int src)
{
priority_queue<iPair, vector<iPair>, greater<iPair> >
pq;
vector<int> dist(V, INF);
pq.push(make_pair(0, src));
dist[src] = 0;
while (!pq.empty()) {
int u = pq.top().second;
pq.pop();
list<pair<int, int> >::iterator i;
for (i = adj[u].begin(); i != adj[u].end(); ++i) {
int v = (*i).first;
int weight = (*i).second;
if (dist[v] > dist[u] + weight) {
dist[v] = dist[u] + weight;
pq.push(make_pair(dist[v], v));
}
}
}
printf("Vertex Distance from Source\n");
for (int i = 0; i < V; ++i)
printf("%d \t\t %d\n", i, dist[i]);
}
int main()
{
int V = 7;
Graph g(V);
g.addEdge(0, 1, 2);
g.addEdge(0, 2, 6);
g.addEdge(1, 3, 5);
g.addEdge(2, 3, 8);
g.addEdge(3, 4, 10);
g.addEdge(3, 5, 15);
g.addEdge(4, 6, 2);
g.addEdge(5, 6, 6);
g.shortestPath(0);
return 0;
}
|
Java
import java.util.ArrayList;
import java.util.Arrays;
import java.util.HashMap;
import java.util.PriorityQueue;
public class DijkstraAlgoForShortestDistance {
static class Node implements Comparable<Node> {
int v;
int distance;
public Node(int v, int distance)
{
this.v = v;
this.distance = distance;
}
@Override public int compareTo(Node n)
{
if (this.distance <= n.distance) {
return -1;
}
else {
return 1;
}
}
}
static int[] dijkstra(
int V,
ArrayList<ArrayList<ArrayList<Integer> > > adj,
int S)
{
boolean[] visited = new boolean[V];
HashMap<Integer, Node> map = new HashMap<>();
PriorityQueue<Node> q = new PriorityQueue<>();
map.put(S, new Node(S, 0));
q.add(new Node(S, 0));
while (!q.isEmpty()) {
Node n = q.poll();
int v = n.v;
int distance = n.distance;
visited[v] = true;
ArrayList<ArrayList<Integer> > adjList
= adj.get(v);
for (ArrayList<Integer> adjLink : adjList) {
if (visited[adjLink.get(0)] == false) {
if (!map.containsKey(adjLink.get(0))) {
map.put(
adjLink.get(0),
new Node(v,
distance
+ adjLink.get(1)));
}
else {
Node sn = map.get(adjLink.get(0));
if (distance + adjLink.get(1)
< sn.distance) {
sn.v = v;
sn.distance
= distance + adjLink.get(1);
}
}
q.add(new Node(adjLink.get(0),
distance
+ adjLink.get(1)));
}
}
}
int[] result = new int[V];
for (int i = 0; i < V; i++) {
result[i] = map.get(i).distance;
}
return result;
}
public static void main(String[] args)
{
ArrayList<ArrayList<ArrayList<Integer> > > adj
= new ArrayList<>();
HashMap<Integer, ArrayList<ArrayList<Integer> > >
map = new HashMap<>();
int V = 6;
int E = 5;
int[] u = { 0, 0, 1, 2, 4 };
int[] v = { 3, 5, 4, 5, 5 };
int[] w = { 9, 4, 4, 10, 3 };
for (int i = 0; i < E; i++) {
ArrayList<Integer> edge = new ArrayList<>();
edge.add(v[i]);
edge.add(w[i]);
ArrayList<ArrayList<Integer> > adjList;
if (!map.containsKey(u[i])) {
adjList = new ArrayList<>();
}
else {
adjList = map.get(u[i]);
}
adjList.add(edge);
map.put(u[i], adjList);
ArrayList<Integer> edge2 = new ArrayList<>();
edge2.add(u[i]);
edge2.add(w[i]);
ArrayList<ArrayList<Integer> > adjList2;
if (!map.containsKey(v[i])) {
adjList2 = new ArrayList<>();
}
else {
adjList2 = map.get(v[i]);
}
adjList2.add(edge2);
map.put(v[i], adjList2);
}
for (int i = 0; i < V; i++) {
if (map.containsKey(i)) {
adj.add(map.get(i));
}
else {
adj.add(null);
}
}
int S = 1;
int[] result
= DijkstraAlgoForShortestDistance.dijkstra(
V, adj, S);
System.out.println(Arrays.toString(result));
}
}
|
Python3
import heapq
class Node:
def __init__(self, v, distance):
self.v = v
self.distance = distance
def __lt__(self, other):
return self.distance < other.distance
def dijkstra(V, adj, S):
visited = [False] * V
map = {}
q = []
map[S] = Node(S, 0)
heapq.heappush(q, Node(S, 0))
while q:
n = heapq.heappop(q)
v = n.v
distance = n.distance
visited[v] = True
adjList = adj[v]
for adjLink in adjList:
if not visited[adjLink[0]]:
if adjLink[0] not in map:
map[adjLink[0]] = Node(v, distance + adjLink[1])
else:
sn = map[adjLink[0]]
if distance + adjLink[1] < sn.distance:
sn.v = v
sn.distance = distance + adjLink[1]
heapq.heappush(q, Node(adjLink[0], distance + adjLink[1]))
result = [0] * V
for i in range(V):
result[i] = map[i].distance
return result
def main():
adj = [[] for _ in range(6)]
V = 6
E = 5
u = [0, 0, 1, 2, 4]
v = [3, 5, 4, 5, 5]
w = [9, 4, 4, 10, 3]
for i in range(E):
edge = [v[i], w[i]]
adj[u[i]].append(edge)
edge2 = [u[i], w[i]]
adj[v[i]].append(edge2)
S = 1
result = dijkstra(V, adj, S)
print(result)
if __name__ == "__main__":
main()
|
C#
using System;
using System.Collections.Generic;
public class Graph {
private int V;
private List<Tuple<int, int> >[] adj;
public Graph(int v)
{
V = v;
adj = new List<Tuple<int, int> >[ v ];
for (int i = 0; i < v; ++i)
adj[i] = new List<Tuple<int, int> >();
}
public void addEdge(int u, int v, int w)
{
adj[u].Add(Tuple.Create(v, w));
adj[v].Add(Tuple.Create(u, w));
}
public void shortestPath(int s)
{
var pq = new PriorityQueue<Tuple<int, int> >();
var dist = new int[V];
for (int i = 0; i < V; i++)
dist[i] = int.MaxValue;
pq.Enqueue(Tuple.Create(0, s));
dist[s] = 0;
while (pq.Count != 0) {
var u = pq.Dequeue().Item2;
foreach(var i in adj[u])
{
int v = i.Item1;
int weight = i.Item2;
if (dist[v] > dist[u] + weight) {
dist[v] = dist[u] + weight;
pq.Enqueue(Tuple.Create(dist[v], v));
}
}
}
Console.WriteLine("Vertex Distance from Source");
for (int i = 0; i < V; ++i)
Console.WriteLine("{0}\t\t{1}", i, dist[i]);
}
}
public class PriorityQueue<T> {
private readonly List<T> _data;
private readonly Comparison<T> _compare;
public PriorityQueue()
: this(Comparer<T>.Default)
{
}
public PriorityQueue(IComparer<T> comparer)
: this(comparer.Compare)
{
}
public PriorityQueue(Comparison<T> comparison)
{
_data = new List<T>();
_compare = comparison;
}
public void Enqueue(T item)
{
_data.Add(item);
var childIndex = _data.Count - 1;
while (childIndex > 0) {
var parentIndex = (childIndex - 1) / 2;
if (_compare(_data[childIndex],
_data[parentIndex])
>= 0)
break;
T tmp = _data[childIndex];
_data[childIndex] = _data[parentIndex];
_data[parentIndex] = tmp;
childIndex = parentIndex;
}
}
public T Dequeue()
{
var lastElement = _data.Count - 1;
var frontItem = _data[0];
_data[0] = _data[lastElement];
_data.RemoveAt(lastElement);
--lastElement;
var parentIndex = 0;
while (true) {
var childIndex = parentIndex * 2 + 1;
if (childIndex > lastElement)
break;
var rightChild = childIndex + 1;
if (rightChild <= lastElement
&& _compare(_data[rightChild],
_data[childIndex])
< 0)
childIndex = rightChild;
if (_compare(_data[parentIndex],
_data[childIndex])
<= 0)
break;
T tmp = _data[parentIndex];
_data[parentIndex] = _data[childIndex];
_data[childIndex] = tmp;
parentIndex = childIndex;
}
return frontItem;
}
public T Peek()
{
T frontItem = _data[0];
return frontItem;
}
public int Count
{
get { return _data.Count; }
}
}
class Program {
static void Main(string[] args)
{
int V = 7;
Graph g = new Graph(V);
g.addEdge(0, 1, 2);
g.addEdge(0, 2, 6);
g.addEdge(1, 3, 5);
g.addEdge(2, 3, 8);
g.addEdge(3, 4, 10);
g.addEdge(3, 5, 15);
g.addEdge(4, 6, 2);
g.addEdge(5, 6, 6);
g.shortestPath(0);
}
}
|
Javascript
class PriorityQueue {
constructor() {
this.queue = [];
}
enqueue(element, priority) {
this.queue.push({ element, priority });
this.queue.sort((a, b) => a.priority - b.priority);
}
dequeue() {
if (this.isEmpty()) {
return null;
}
return this.queue.shift().element;
}
isEmpty() {
return this.queue.length === 0;
}
}
class Graph {
constructor(V) {
this.V = V;
this.adj = new Array(V);
for (let i = 0; i < V; i++) {
this.adj[i] = [];
}
}
addEdge(u, v, w) {
this.adj[u].push({ v, w });
this.adj[v].push({ v: u, w });
}
shortestPath(src) {
const pq = new PriorityQueue();
const dist = new Array(this.V).fill(Infinity);
const visited = new Array(this.V).fill(false);
pq.enqueue(src, 0);
dist[src] = 0;
while (!pq.isEmpty()) {
const u = pq.dequeue();
if (visited[u]) continue;
visited[u] = true;
for (const { v, w } of this.adj[u]) {
if (!visited[v] && dist[u] + w < dist[v]) {
dist[v] = dist[u] + w;
pq.enqueue(v, dist[v]);
}
}
}
console.log("Vertex Distance from Source");
for (let i = 0; i < this.V; i++) {
console.log(`${i}\t\t${dist[i] === Infinity ? "Infinity" : dist[i]}`);
}
}
}
function main() {
const V = 7;
const g = new Graph(V);
g.addEdge(0, 1, 2);
g.addEdge(0, 2, 6);
g.addEdge(1, 3, 5);
g.addEdge(2, 3, 8);
g.addEdge(3, 4, 10);
g.addEdge(3, 5, 15);
g.addEdge(4, 6, 2);
g.addEdge(5, 6, 6);
g.shortestPath(0);
}
main();
|
Final Answer:
.png)
Output
Complexity Analysis of Dijkstra Algorithm:
- Time complexity: O((V + E) log V), where V is the number of vertices and E is the number of edges.
- Auxiliary Space: O(V), where V is the number of vertices and E is the number of edges in the graph.
2. Array-based Implementation of Dijkstra’s Algorithm (Naive Approach):
Dijkstra’s Algorithm can also be implemented using arrays without using a priority queue. This implementation is straightforward but can be less efficient, especially on large graphs.
The algorithm proceeds as follows:
- Initialize an array to store distances from the source to each node.
- Mark all nodes as unvisited.
- Set the distance to the source node as 0 and infinity for all other nodes.
- Repeat until all nodes are visited:
- Find the unvisited node with the smallest known distance.
- For the current node, update the distances of its unvisited neighbors.
- Mark the current node as visited.
Complexity Analysis:
- Time Complexity: O(V^2) in the worst case, where V is the number of vertices. This can be improved to O(V^2) with some optimizations.
- Auxiliary Space: O(V), where V is the number of vertices and E is the number of edges in the graph.
Dijkstra’s algorithm and Bellman-Ford algorithm are both used to find the shortest path in a weighted graph, but they have some key differences. Here are the main differences between Dijkstra’s algorithm and Bellman-Ford algorithm:
| Feature: |
Dijkstra’s |
Bellman Ford |
| Optimization |
optimized for finding the shortest path between a single source node and all other nodes in a graph with non-negative edge weights |
Bellman-Ford algorithm is optimized for finding the shortest path between a single source node and all other nodes in a graph with negative edge weights. |
| Relaxation |
Dijkstra’s algorithm uses a greedy approach where it chooses the node with the smallest distance and updates its neighbors |
the Bellman-Ford algorithm relaxes all edges in each iteration, updating the distance of each node by considering all possible paths to that node |
| Time Complexity |
Dijkstra’s algorithm has a time complexity of O(V^2) for a dense graph and O(E log V) for a sparse graph, where V is the number of vertices and E is the number of edges in the graph. |
Bellman-Ford algorithm has a time complexity of O(VE), where V is the number of vertices and E is the number of edges in the graph. |
| Negative Weights |
Dijkstra’s algorithm does not work with graphs that have negative edge weights, as it assumes that all edge weights are non-negative. |
Bellman-Ford algorithm can handle negative edge weights and can detect negative-weight cycles in the graph. |
Dijkstra’s algorithm and Floyd-Warshall algorithm are both used to find the shortest path in a weighted graph, but they have some key differences. Here are the main differences between Dijkstra’s algorithm and Floyd-Warshall algorithm:
| Feature: |
Dijkstra’s |
Floyd-Warshall Algorithm |
| Optimization |
Optimized for finding the shortest path between a single source node and all other nodes in a graph with non-negative edge weights |
Floyd-Warshall algorithm is optimized for finding the shortest path between all pairs of nodes in a graph. |
| Technique |
Dijkstra’s algorithm is a single-source shortest path algorithm that uses a greedy approach and calculates the shortest path from the source node to all other nodes in the graph. |
Floyd-Warshall algorithm, on the other hand, is an all-pairs shortest path algorithm that uses dynamic programming to calculate the shortest path between all pairs of nodes in the graph. |
| Time Complexity |
Dijkstra’s algorithm has a time complexity of O(V^2) for a dense graph and O(E log V) for a sparse graph, where V is the number of vertices and E is the number of edges in the graph. |
Floyd-Warshall algorithm, on the other hand, is an all-pairs shortest path algorithm that uses dynamic programming to calculate the shortest path between all pairs of nodes in the graph. |
| Negative Weights |
Dijkstra’s algorithm does not work with graphs that have negative edge weights, as it assumes that all edge weights are non-negative. |
Floyd-Warshall algorithm, on the other hand, is an all-pairs shortest path algorithm that uses dynamic programming to calculate the shortest path between all pairs of nodes in the graph. |
Dijkstra’s Algorithm vs A* Algorithm
Dijkstra’s algorithm and A* algorithm are both used to find the shortest path in a weighted graph, but they have some key differences. Here are the main differences between Dijkstra’s algorithm and A* algorithm:
| Feature: |
|
A* Algorithm |
| Search Technique |
Optimized for finding the shortest path between a single source node and all other nodes in a graph with non-negative edge weights |
A* algorithm is an informed search algorithm that uses a heuristic function to guide the search towards the goal node. |
| Heuristic Function |
Dijkstra’s algorithm, does not use any heuristic function and considers all the nodes in the graph. |
A* algorithm uses a heuristic function that estimates the distance from the current node to the goal node. This heuristic function is admissible, meaning that it never overestimates the actual distance to the goal node |
| Time Complexity |
Dijkstra’s algorithm has a time complexity of O(V^2) for a dense graph and O(E log V) for a sparse graph, where V is the number of vertices and E is the number of edges in the graph. |
The time complexity of A* algorithm depends on the quality of the heuristic function. |
| Application |
Dijkstra’s algorithm is used in many applications such as routing algorithms, GPS navigation systems, and network analysis |
. A* algorithm is commonly used in pathfinding and graph traversal problems, such as video games, robotics, and planning algorithms. |
Practice Problems on Dijkstra’s Algorithm:
- Dijkstra’s shortest path algorithm | Greedy Algo-7
- Dijkstra’s Algorithm for Adjacency List Representation | Greedy Algo-8
- Dijkstra’s Algorithm – Priority Queue and Array Implementation
- Dijkstra’s shortest path algorithm using set in STL
- Dijkstra’s shortest path algorithm using STL in C++
- Dijkstra’s Shortest Path Algorithm using priority_queue of STL
- Dijkstra’s shortest path algorithm using matrix in C++
- Dijkstra’s Algorithm for Single Source Shortest Path in a DAG
- Dijkstra’s Algorithm using Fibonacci Heap
- Dijkstra’s shortest path algorithm for directed graph with negative weights
- Printing Paths in Dijkstra’s Shortest Path Algorithm
- Dijkstra’s shortest path algorithm with priority queue in Java
- Dijkstra’s shortest path algorithm with adjacency list in Java
- Dijkstra’s shortest path algorithm using adjacency matrix in Java
- Dijkstra’s Algorithm using Adjacency List in Python
- Dijkstra’s Algorithm using PriorityQueue in Python
- Dijkstra’s Algorithm using heapq module in Python
- Dijkstra’s Algorithm using dictionary and priority queue in Python
Conclusion:
Overall, Dijkstra’s Algorithm is a simple and efficient way to find the shortest path in a graph with non-negative edge weights. However, it may not work well with graphs that have negative edge weights or cycles. In such cases, more advanced algorithms such as the Bellman-Ford algorithm or the Floyd-Warshall algorithm may be used.
Share your thoughts in the comments
Please Login to comment...