Figures on the Same Base and between the Same Parallels
Last Updated :
24 Jun, 2022
A triangle is a three-sided polygon and a parallelogram is a four-sided polygon or simply a quadrilateral that has parallel opposite sides. We encounter these two polynomials almost everywhere in our everyday lives. For example: Let’s say a farmer has a piece of land that is in the shape of a parallelogram. He wants to divide this land into two parts for his daughters. Now when divided into two parts, it will generate two triangles. So, in this case, it becomes essential for us to know their areas. Simple formulas to calculate the areas of triangles and parallelograms can be sometimes cumbersome. So, we use some theorems and properties to simplify our calculations in such scenarios. Let’s look at these properties in detail.
Parallelograms and Triangles
Triangles have three sides and parallelograms are the quadrilaterals that have four sides while the opposite sides are parallel to each other. The figure below shows a parallelogram and a triangle. Let’s say “b2” and “h2″ is the length of the base and height of the triangle respectively and “b1″ and “h1” are the base and height of the parallelogram.

Area of triangle = 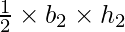
Area of parallelogram = 
Congruent Figures and Their Areas
We know that two figures are called congruent if they have the same size and shape. So if two figures are congruent, you can superimpose them over each other and both will completely cover the other figure. That means that if any two figures are congruent, their areas must be equal. But notice that the converse of this statement is not true, if two figures have equal areas, it is not necessary that both are congruent. In the figure below, we can see two pairs of figures which are congruent and have the same areas, but the other pair of figures have the same areas, but they are not congruent.

Two Congruent figures with the same area

In the above figure, let’s compare the areas of two quadrilaterals.
Ar(PQRS) = 9 × 4 = 36
Ar(TUVW) = 62 = 36
Notice that both have the same area, but they are not congruent. This verifies that the converse of our statement that we gave earlier is not true. So, now the definition of the area can be summarized as follows,
Area of a figure is the measure of the plane that is enclosed by that figure. It has following two properties:
- Let’s say we have two figures X and Y. If X and Y are congruent figures, then ar(X) = ar(Y).
- If both figure combine without overlapping to make another figure T. Area of figure T will be given by, ar(T) = ar(X) + ar(Y).
Parallelograms on the same Base and Between the Same Parallels
Our goal is to learn about the relation between the areas of two parallelograms when they have the same base and are between the same parallels. The figure below shows two parallelograms with a common base and between the same parallel lines. Let’s prove the relation between these areas with some theorems.

Theorem: Parallelograms with the same base and between the same parallels have the same area.
Proof:
Let’s assume we have two parallelograms PQRS and RSTU as shown in the figure below. Both have the same base RS and are between same parallels. The objective is to prove that ar(PQRS) = ar(RSTU).

In the figure, RSTQ is common to both the parallelograms. Now, if we can prove that ar(PST) = ar(QRU). We can prove that areas of both parallelograms are equal.
Let’s look at the triangle PST and QRU.
∠SPT = ∠RQU (Corresponding angles)
∠PTS = ∠QUR (Corresponding angles)
Now since two angles of triangles are equal, the third angle will also be equal due to angle sum property.
∠PST = ∠QRU
Now both of these triangles are congruent
ΔPST≅ ΔQRU
Thus, ar(PST) = ar(QRU)
Now we know that,
Ar(PQRS) = ar(RSTQ) + ar(PST)
Ar(RSTU) = ar(RSTQ) + ar(QRU)
Since ar(RSTQ) is common and ar(PST) = ar(QRU).
Thus, ar(PQRS) = ar(RSTU)
Triangles on the same Base and Between the Same Parallels
The figure below represents two triangles that are on the same base and are between the same parallels. Our goal is to find the relation between the areas of these two triangles. Let’s see theorems related to

Theorem: Two triangles on the same base and between the same parallels have equal area.
Proof:

We know that area of triangle is given by 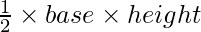
So, two triangles will have same area if they have same base and height.
Our triangles have a common base. Now since they are between two parallels, they must have the same height. Thus, both the triangles have same area.
Sample Questions
Question 1: Find the area of the triangle and parallelogram given in the figures below.

Solution:
We know,
Area of triangle = 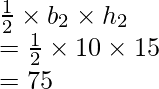
Area of parallelogram = b2 × h2
= 3 × 5
= 15
Question 2: State three properties of a parallelogram.
Answer:
Three properties of parallelogram:
- Opposite sides are parallel and equal.
- Opposite angles are equal.
- Adjacent Angles sum up to 180°.
Question 3: In the triangle ΔPQR given in the figure below, PS is the median. Prove that ar(PSR) = ar(PQS).

Answer:
Now if we draw a perpendicular from the vertex P to the base QR. We’ll see that this perpendicular is common to both the triangle. Thus, both of them have same base and same height. So, they must have the same area.
Question 4: In the figure given below, we have a rectangle RSTU and a parallelogram PQRS. It is given that, PL is perpendicular to RS. Now, prove:
- Ar(RSTU) = ar(PQRS)
- Ar(PQRS) = RS x AL.

Solution:
1. We know that rectangles are also parallelograms. So, the theorem we studied also apply on the rectangle. Both of these figures have same base and lie between same parallels. Thus, both should have the same area.
Ar(RSTU) = ar(PQRS)
2. The area of parallelogram = base x height.
Ar(PQRS) = RU x RS
Since, PURL is also a rectangle, RU = AL. Thus,
Ar(PQRS) = RS x AL.
Question 5: A farmer has a field that is in the shape of a parallelogram PQRS. The farmer takes a point on RS and joins it to P, Q. Answer the following questions:
- How many portions does he have now in the field?
- He wants to sow corn and sugarcane, which portions he should use so that both are grown in the same area.

Solution:
1. Let the point farmer chose to be X. Join X to P and Q. This divides the field into three parts.

2. Now, we know that the if a triangle and a parallelogram have same base and are in between same parallels. Then, area of triangle is half of the area of the parallelogram.
So, in this case, ar(XPQ) = 1/2(ar(PQRS)
So, the remaining two portions must make the other half of the area. That means,
Ar(XPQ) = ar(XPS) + ar(XQR)
So, he should grow one crop in XPQ and other crop in both XPS and XQR.
Share your thoughts in the comments
Please Login to comment...