Significant Figures
Last Updated :
01 Sep, 2023
In Order to find the value of different sizes and compare them, measurement is used. Measuring things is not only a concept but also practically used in everyday life, for example, a milkman measures milk before selling it in order to make sure the correct amount is served, A tailor always measures the size of the body before making suit, A cobbler measures the size of the foot before making/giving the sole for the shoes, and so many other examples are available around us to prove the significance of measurement.
What is Measurement?
Measurement is comparing the quantity to be measured with the standard quantity available. Measurement is one topic that is not only taught in math but also in Physics and Chemistry since every subject requires an understanding of measurement, in order to measure the quantities.
Measuring a quantity does not always give a perfectly accurate answer. Only Ideal measuring instruments can provide a perfectly accurate answer. Practically measurement leads to two parts of an answer called reliable digits and uncertain digits.
Significant Figures
Significant Figures or Significant Digits are defined as the numbers that contain all certain figures and the first uncertain figure. For example, the length of an object is measured as 123.5m, here 1, 2, and 3 are certain digits and 5 is the uncertain digit, hence, Significant digits are 4 in this case.
If the value of a quantity has more than the significant digits assigned for the value, the value of the quantity is sure to be flawed and misleading. This is the reason why Errors are taught. Significant figures are known as the resolution of the measurement.

Rules to Determine Significant Figures
- All the non-Zero digits are considered as Significant Figures.
For example, 67812 has 5 significant figures.
- All the Zeros that lie between two non-zero digits are also considered significant irrespective of the decimal position in the value.
For example, 1.03 have 3 significant figures.
- If the zeros are present on the rightmost side of a value that is not a decimal value, the zeros will not be considered as significant figures.
For example, 25000 has 2 significant figures.
- If the digit is less than 1, two things are to be noticed here. First, the zeros present at the very end of the value are not considered significant figures. Second, the zeros on the left of the non-zero digits are considered significant.
For example, 0.067 (here 2 zeroes are present on the left side, are considered significant in nature)
- If the value is decimal in nature, the trailing zeros are considered significant figures.
For example, 2.30 has 3 significant figures.
Rules For Applying Arithmetic Operations on Significant Figures
Two values when they go arithmetic operation, the final value obtained will always have more significant figures obtained. Say, in order to determine the current in a circuit, the resistance and voltage are given as 6.77ohm and 12.559volts. The current obtained will be 1.8550960118168, the value of current has a lot more significant figures as compared to the values of voltage and resistance, but it is known that when some operation is done on two quantity containing errors, the final result will sure to have more errors than the given quantities. Therefore, certain rules are made to understand the significant figures when they undergo any arithmetic operation,
- While dividing or multiplying, the final value obtained must have the same amount of significant figures as the amount in the input value (the input value with less significant figures).
For example, Take the previous example where R= 6.77ohm and V= 12.559volts, the current is described as,
I = V/R
I = 12.559/6.77
I = 1.850960118168amperes
According to the rule, I should have 3 significant digits, that is, I= 1.85 amperes.
- While adding or Subtracting, the final result obtained should have as many significant figures as are present in the input value with the least significant figures.
For example, Take Inputs as 4.556 and 7.9864. If addition is done on these two inputs, the result is 12.5424. However, the result should be considered as 12.54.
Important Points to keep in mind while determining significant figures:
- The change in the unit of a value will not change the significant digit.
For example: 23m = 2300cm = 230000 mm, They all have 2 significant digits.
- It is better to use scientific notation while denoting measurements. The notation must be a × 10b.
For example, Take the above example, 23m = 2.3 × 101 m= 2.3 ×103 cm= 2.3 × 105 mm. In all the case, significant digit will come out to be 2.
- If the exact digit is divided or multiplied, it will give infinite significant digits.
Sample Questions on Significant Figures
Question 1: Determine the significant figures in the following quantities,
- 232
- 1.500
- 0.0899
- 5.6 × 103
- 85633.98
Answer:
Based on the rules provided for determining significant digits,
- 232= 3 significant figures
- 1.500= 4 significant figures
- 0.0899= 5 significant figures
- 5.6 × 103 = 2 Significant figures
- 85633.98 = 7 Significant figures.
Question 2: Two digits, 33. 689 and 44. 23 are added together. Find the significant figures in the resultant value obtained.
Answer:
Adding 33.689 and 44.23, this will give 77.919. But the input value with the least significant digit is 44. 23. Therefore, the answer is 77.91.
Question 3: The mass of an object is 50.9kgs and the volume is 2.34m3. Find the Density of the object based on the significant figure rule.
Solution:
Density of an object is defined as,
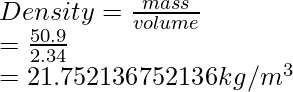
Since, the least significant value in the input is 3.
Hence, the density of the object is 21.7kg/m3.
Question 4: Two Values are multiplied to obtain a certain value as a result. The input values are 3.99 and 1.5789, Find the Significant digits of the resultant value obtained.
Answer:
The input values do not even needed to be added in order to find the significant figure of the resultant value as there is an easier way. Just by looking as the rules, it can be seen that the first rule of arithmetic operations of significant figures says that the resultant value has the same significant digits as found in the input with the least significant digit.
Therefore, The result will have 3 significant digits.
Question 5: What is the difference between 0.06700 and 6.700?
Answer:
The difference is due to the fact that 0.06700 is a number less than 1 and hence, the zeros on the left are significant, but the zeroes on the rightmost side are insignificant (rule 4). The significant digits are 4.
While, the number 6.700 is a number greater than 1 and also a decimal, therefore, the zeroes on the rightmost side are significant (rule 5). The significant digits are 4.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...