Different Operations on Matrices
Last Updated :
06 Jan, 2023
For an introduction to matrices, you can refer to the following article: Matrix Introduction
In this article, we will discuss the following operations on matrices and their properties:
- Matrices Addition
- Matrices Subtraction
- Matrices Multiplication
Matrices Addition:
The addition of two matrices A m*n and Bm*n gives a matrix Cm*n. The elements of C are the sum of corresponding elements in A and B which can be shown as:

Key points:
- The addition of matrices is commutative, which means A+B = B+A
- The addition of matrices is associative, which means A+(B+C) = (A+B)+C
- The order of matrices A, B, and A+B is always the same
- If the order of A and B are different, A+B can’t be computed
- The complexity of the addition operation is O(M*N) where M*N is the order of matrices
Implementation of the above approach:
C++
#include <iostream>
using namespace std;
int main()
{
int n = 2, m = 2;
int a[n][m] = { { 2, 5 }, { 1, 7 } };
int b[n][m] = { { 3, 7 }, { 2, 9 } };
int c[n][m];
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++) {
c[i][j] = a[i][j] + b[i][j];
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++)
cout << c[i][j] << " ";
cout << endl;
}
}
|
Java
import java.util.*;
class GFG
{
public static void main(String[] args)
{
int n = 2, m = 2;
int a[][] = { { 2, 5 }, { 1, 7 } };
int b[][] = { { 3, 7 }, { 2, 9 } };
int c[][] = new int[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++)
c[i][j] = a[i][j] + b[i][j];
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++)
System.out.print(c[i][j] + " ");
System.out.print("\n");
}
}
}
|
Python3
N = 4
a = [ [2, 5],
[1, 7]]
b= [ [3, 7],
[2, 9]]
N = 2
c=a[:][:]
for i in range(N):
for j in range(N):
c[i][j] = a[i][j] + b[i][j]
for i in range(N):
for j in range(N):
print(c[i][j], " ", end='')
print()
|
C#
using System;
class GFG {
static public void Main()
{
int N = 2;
int M = 2;
int[,] a = { { 2, 5 }, { 1, 7 } };
int[,] b = { { 3, 7 }, { 2, 9 } };
int [,] c =new int[N,M];
for (int i = 0; i < N; i++)
for (int j = 0; j < M; j++) {
c[i,j] = a[i,j] + b[i,j];
}
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++)
Console.Write(c[i,j] + " ");
Console.WriteLine();
}
}
}
|
Javascript
<script>
var n = 2, m = 2;
var a = [[ 2, 5 ], [ 1, 7 ]];
var b = [[ 3, 7 ], [ 2, 9 ]];
var c = Array.from(Array(n), ()=>Array(m).fill(0));
for (var i = 0; i < n; i++)
for (var j = 0; j < n; j++) {
c[i][j] = a[i][j] + b[i][j];
}
for (var i = 0; i < n; i++) {
for (var j = 0; j < n; j++)
document.write( c[i][j] + " ");
document.write("<br>");
}
</script>
|
Complexity analysis:
- Time Complexity: O(N*M)
- Auxiliary Space: O(N*M)
Matrices Subtraction:
The subtraction of two matrices Am*n and Bm*n give a matrix Cm*n. The elements of C are difference of corresponding elements in A and B which can be represented as:

Key points:
- Subtraction of matrices is non-commutative which means A-B ≠ B-A
- Subtraction of matrices is non-associative which means A-(B-C) ≠ (A-B)-C
- The order of matrices A, B, and A – B is always the same
- If the order of A and B are different, A – B can’t be computed
- The complexity of subtraction operation is O(M*N) where M*N is the order of matrices
Implementation of the above approach:
C++
#include <iostream>
using namespace std;
int main()
{
int n = 2, m = 2;
int a[n][m] = { { 2, 5 }, { 1, 7 } };
int b[n][m] = { { 3, 7 }, { 2, 9 } };
int c[n][m];
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++) {
c[i][j] = a[i][j] - b[i][j];
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++)
cout << c[i][j] << " ";
cout << endl;
}
}
|
Java
public class GFG {
public static void main(String[] args)
{
int n = 2;
int m = 2;
int[][] a = { { 2, 5 }, { 1, 7 } };
int[][] b = { { 3, 7 }, { 2, 9 } };
int[][] c = new int[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
c[i][j] = a[i][j] - b[i][j];
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.print(c[i][j]);
System.out.print(" ");
}
System.out.print("\n");
}
}
}
|
Python3
N = 4
a = [[2, 5],
[1, 7]]
b = [[3, 7],
[2, 9]]
N = 2
c = a[:][:]
for i in range(N):
for j in range(N):
c[i][j] = a[i][j] - b[i][j]
for i in range(N):
for j in range(N):
print(c[i][j], " ", end='')
print()
|
C#
using System;
class GFG {
static public void Main()
{
int N = 2;
int M = 2;
int[,] a = { { 2, 5 }, { 1, 7 } };
int[,] b = { { 3, 7 }, { 2, 9 } };
int [,] c =new int[N,M];
for (int i = 0; i < N; i++)
for (int j = 0; j < M; j++) {
c[i,j] = a[i,j] - b[i,j];
}
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++)
Console.Write(c[i,j] + " ");
Console.WriteLine();
}
}
}
|
Javascript
<script>
var n = 2, m = 2;
var a = [[ 2, 5 ], [ 1, 7 ]];
var b = [[ 3, 7 ], [ 2, 9 ]];
var c = Array.from(Array(n), ()=>Array(m).fill(0));
for (var i = 0; i < n; i++)
for (var j = 0; j < n; j++) {
c[i][j] = a[i][j] - b[i][j];
}
for (var i = 0; i < n; i++) {
for (var j = 0; j < n; j++)
document.write( c[i][j] + " ");
document.write("<br>");
}
</script>
|
Complexity Analysis:
- Time Complexity: O(N*M)
- Auxiliary Space: O(N*M)
Matrices Multiplication:
The multiplication of two matrices Am*n and Bn*p give a matrix Cm*p. It means a number of columns in A must be equal to the number of rows in B to calculate C=A*B. To calculate element c11, multiply elements of 1st row of A with 1st column of B and add them (5*1+6*4) which can be shown as:
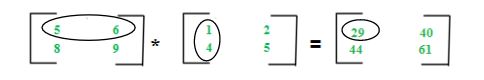
Key points:
- Multiplication of matrices is non-commutative which means A*B ≠ B*A
- Multiplication of matrices is associative which means A*(B*C) = (A*B)*C
- For computing A*B, the number of columns in A must be equal to the number of rows in B
- The existence of A*B does not imply the existence of B*A
- The complexity of multiplication operation (A*B) is O(m*n*p) where m*n and n*p are the order of A and B respectively
- The order of matrix C computed as A*B is m*p where m*n and n*p are the order of A and B respectively
Implementation of the above approach:
C++
#include <iostream>
using namespace std;
int main()
{
int n = 2, m = 2;
int a[n][m] = { { 2, 5 }, { 1, 7 } };
int b[n][m] = { { 3, 7 }, { 2, 9 } };
int c[n][m];
int i, j, k;
for (i = 0; i < n; i++)
{
for (j = 0; j < n; j++)
{
c[i][j] = 0;
for (k = 0; k < n; k++)
c[i][j] += a[i][k] * b[k][j];
}
}
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
cout << c[i][j] << " ";
cout << endl;
}
}
|
Java
import java.io.*;
class GFG {
public static void main(String[] args)
{
int n = 2, m = 2;
int a[][] = { { 2, 5 }, { 1, 7 } };
int b[][] = { { 3, 7 }, { 2, 9 } };
int c[][] = new int[n][m];
int i, j, k;
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
c[i][j] = 0;
for (k = 0; k < n; k++) {
c[i][j] += a[i][k] * b[k][j];
}
}
}
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
System.out.print(c[i][j] + " ");
}
System.out.println();
}
}
}
|
Python
a = [[2, 5], [1, 7]]
b = [[3, 7], [2, 9]]
c = [[0, 0], [0, 0]]
for i in range(0, 2):
for j in range(0, 2):
c[i][j] = 0
for k in range(0, 2):
c[i][j] = c[i][j]+(a[i][k]*b[k][j])
for i in range(0, 2):
for j in range(0, 2):
print(c[i][j])
|
C#
using System;
class GFG {
static public void Main()
{
int N = 2;
int M = 2;
int[,] a = { { 2, 5 }, { 1, 7 } };
int[,] b = { { 3, 7 }, { 2, 9 } };
int [,] c =new int[N,M];
for (int i = 0; i < N; i++)
{
for (int j = 0; j < M; j++) {
c[i,j]=0;
for(int k=0;k<N;k++)
c[i,j] = c[i,j]+(a[i,k] * b[k,j]);
}
}
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++)
Console.Write(c[i,j] + " ");
Console.WriteLine();
}
}
}
|
Javascript
<script>
var n = 2, m = 2;
var a = [[ 2, 5 ], [ 1, 7 ]];
var b = [[ 3, 7 ], [ 2, 9 ]];
var c = Array.from(Array(n), ()=>Array(m).fill(0));
for (var i = 0; i < n; i++){
for (var j = 0; j < n; j++) {
c[i][j] = 0;
for (var k = 0; k < n; k++) {
c[i][j] += a[i][k] * b[k][j];
}
}}
for (var i = 0; i < n; i++) {
for (var j = 0; j < n; j++)
document.write( c[i][j] + " ");
document.write("<br>");
}
</script>
|
Complexity Analysis:
- Time Complexity: O((N2)*M)
- Auxiliary Space: O(N*M)
Share your thoughts in the comments
Please Login to comment...