Parametric Differentiation refers to the differentiation of a function in which the dependent and independent variables are equated to a third variable. Derivatives of the functions express the rate of change in the functions. We know how to calculate the derivatives for standard functions. Chain rule, Product rule, and Quotient rule are used to calculate the derivatives of the complex functions which are made up of composition from two or more functions. These functions have two variables that are related to each other in an implicit or explicit manner.
Sometimes we encounter functions in which variables are not related to each other implicitly or explicitly, instead, they are related to each other through a third variable. In this case, we use Parametric Differentiation, which we study in Class 12 for the first time. This article helps in the introduction of the topic to everyone. Here we discussed Parametric Differentiation in detail including methods to find the derivative of a function in parametric form, as well as various other solved examples.
What is Parametric Differentiation?
Parametric Differentiation or Derivative of Function in Parametric Form is the process of finding the derivative of a function in which the dependent variable ‘y‘ and the independent variable ‘x‘ are equated to a third independent variable ‘t‘.
Most often we come across a function that is given straightforwardly manner that y is directly dependent on x i.e. y = f(x) so finding the derivative becomes easy and we easily differentiate y with respect to x and calculate dy/dx. Sometimes we have a function in implicit form i.e. both x and y variables are present in the function and the function is given as f(x, y) in this case we either convert the function into explicit form or apply implicit differentiation.
In Parametric Differentiation, since the variables are connected to each other via a third variable we first differentiate the variables x and y with respect to the third independent variable and their find the ratio of their derivative.
Parametric Equation
Parametric Equation is a equation in which the two variables are equated to a third variable usually denoted by ‘t’. This third variable is called parameter and hence the name is Parametric Equation. This type of equation is usually used in replacing the coordinates from the cartesian form of equation of a curve and convert it into a variable form called as parametric form.
In Parametric Function the two variables are given as x = f(t) and y = g(t) i.e. both are a function of another independent variable ‘t’.
How to Find Derivatives of Functions in Parametric Forms?
Let’s say we have two variables x and y, usually, such variables are related to each other in an implicit or an explicit manner. But in some cases, these variables are related to each other through a third variable. This form is called the parametric form of the equation and the variable is called a parameter. We have x = f(t) and y = g(t) here, t is a parameter.
We will first differentiate x and y with respect to ‘t’ separatly. On differentiating x with respect to ‘t’ we get dx/dt and on differentiating y by ‘t’ we get dy/dt.
Now to the derivative of y with respect to x is given by the formula dy/dx = (dy/dt).(dt/dx). The formula for parametric differentiation is also expressed in the image attached below:

The derivative of such functions is given by chain rule,
Using Chain Rule, dy/dt can be written as
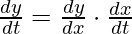
Now, rearranging the terms, we get
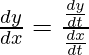 , where
, where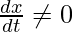
Thus,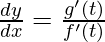 [as
[as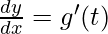 and
and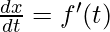 ]
]
Proof of Parametric Differentiation Formula
Since y and x are dependent on ‘t’, then any change in ‘t’ would also cause a change in ‘y’ and ‘x’. Hence, for small change in ‘t’ given as Δt the corresponding changes in x and y are Δx and Δy.
We can write Δy/Δx = (Δy/Δt)/(Δx/Δt)
Taking limit on both sides
lim Δx→0 Δy/Δx = lim Δt→0 (Δy/Δt)/lim Δt→0 (Δx/Δt)
Using the Concept of Limit and Derivatives, we have
dy/dx = (dy/dt)/(dx/dt)
Read More,
Parametric Differentiation Examples
Example 1: Find dy/dx, if x = acos(θ) , y = asin(θ).
Solution:
x = acos(θ) and y = asin(θ)
dx/dθ = −sin(θ)
dy/dθ = a cosθ
Now, let’s find out
dy/dx = (dy/dt)/(dx/dt)
⇒ dy/dx = (dy/dθ)/(dx/dθ)
⇒ dy/dx = acosθ/-asinθ
⇒ dy/dx = -cot θ
Example 2: Find dy/dx, if x = acos2(θ) , y = asin2(θ).
Solution:
x = acos2(θ) , y = asin2(θ)
dx/dθ = -2acosθsinθ
dy/dθ = 2acosθsinθ
Now, let’s find out
dy/dx = (dy/dt)/(dx/dt)
⇒ dy/dx = (dy/dθ)/(dx/dθ)
⇒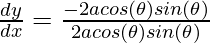
⇒ dy/dx = -1
Example 3: Find dy/dx, if x = at2 + 2t, y = t at t = 0.
Solution:
x = at2 + 2t, y = t
dx/dt = 2at + 2
dy/dt = 2
Now, let’s find out
dy/dx = (dy/dt)/(dx/dt)
⇒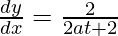
⇒ dy/dx = 2/2
⇒ dy/dx = 1
Example 4: Find dy/dx, if x = at3 + 2t2, y = t2 at t = 1.
Solution:
x = at3 + 2t2, y = t2
dx/dt = 3at2 + 4t
dy/dt = 2t
Now, let’s find out
dy/dx = (dy/dt)/(dx/dt)
⇒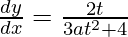
⇒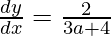
Example 5: Find dy/dx, if x = 4t, y = 1/t at t = 1.
Solution:
x = 4t, y = 1/t
dx/dt = 4
dy/dt = -1/t2
Now, let’s find out
dy/dx = (dy/dt)/(dx/dt)
⇒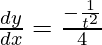
⇒ dy/dx = -1/4t2
At t = 1
dy/dx = -1/4
Example 6: Find dy/dx, if x = 4et, y = cos(t)at t = 1.
Solution:
x = 4et, y =cos(t)
dx/dt = 4et
dy/dt = -sin(t)
Now, let’s find out\
dy/dx = (dy/dt)/(dx/dt)
⇒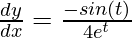
At t = 1
⇒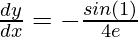
Example 7: Find dy/dx, if x = et + sin(t), y = t2, at = 0.
Solution:
x = et + sin(t), y =t2
dx/dt = et + cos(t)
dy/dt = 2t
Now, let’s find out
dy/dx = (dy/dt)/(dx/dt)
⇒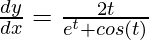
At t = 0
⇒ dy/dx = 0
Example 8: Find dy/dx , if x = tsin(t), y = cos(t), at t = π/2
Solution:
x = tsin(t), y = cos(t)
dx/dt = t.cos(t) + sin(t)
dy/dt = -sin(t)
Now, let’s find out
dy/dx = (dy/dt)/(dx/dt)
⇒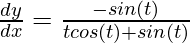
At t = π/2
⇒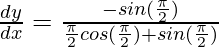
⇒ dy/dx = -1
Example 9: Find dy/dx if x = 4t2 + 10, y =t2at t = 1.
Solution:
x = 4t2 + 10, y =t2
dx/dt = 8t
dy/dt = 2t
Now, let’s find out
dy/dx = (dy/dt)/(dx/dt)
⇒ dy/dx = 2t/8t
At t = 1
dydx = 1/4
Example 10: Find dy/dx if x = at2, y =2at at t = 1.
Solution:
x = at2, y =2at
dx/dt = 2at
dy/dt = 2a
Now, let’s find out
dy/dx = (dy/dt)/(dx/dt)
dy/dx = 2a/2at
At t = 1
dy/dx = 1
Practice Questions on Parametric Differentiation
Q1: Find dy/dx if x = sin2t and y = cos3t
Q2: Find dy/dx if x = at3 and y = 3at
Q3: Find dy/dx if x = 3 log t and y = e2t
Q4: Find dy/dx if x = a sec θ and y = b tan θ
FAQs on Parametric Differentiation
1. What is Parametric Function?
A function in which the two variables are connected to each other via a parameter let’s say ‘t’ is called a Parametric Function.
2. How to Calculate the Derivative of a Parametric Function?
To calculate the derivative of a Parametric Function we need to first find the derivative of x and y with respect to parameter ‘t’ and then take the ratio of their derivatives.
3. What is Parametric Differentiation Formula?
If the functions are given as x = f(t) and y = g(t) then we first need to find dx/dt and dy/dt and the dy/dx = (dy/dt)/(dx/dt)
4. What is an Example of a Parametric Function?
A curve or function defined as y = sin t and x = cos t, is the example of a parametric function. This function defines a unit circle.
Share your thoughts in the comments
Please Login to comment...