Computation of New Profit Sharing Ratio: Retirement of a Partner
Last Updated :
05 Apr, 2023
Whenever a partner retires from a firm, his/her share of profit is acquired either by all the remaining partners or some/ one of them. This leads to a change in Profit-Sharing Ratio among the continuing partners, and therefore, a New Profit-Sharing Ratio for each remaining partner is determined. A New Profit-Sharing Ratio in case of the retirement of a partner is a ratio in which continuing partners agree to share the future profits and losses. Due to the fact that the share of the retiring partner is acquired by all or some of the continuing partners, a New Profit-Sharing Ratio of the remaining partner is nothing but a sum total of the old share of the partner and the share acquired by the partner. Thus, New Share of a Partner = Old Share + Share Acquired by the Partner.
Computation:
Case 1: When a Partner retires, and nothing is mentioned about the New Ratio of the Remaining Partners:
Under such circumstances, where one of the partners retires, and there is no information regarding the new profit-sharing ratio among the remaining partners, it is presumed that the remaining partners shall continue to share the future profits and losses in their old ratio. The remaining partners acquire the share of the retiring partner in their old profit-sharing ratio, which means that the profit-sharing ratio among the remaining partners will be the same.
Steps to determine the New Profit-Sharing Ratio:
Step 1: Convert the old profit-sharing ratio into the simplest form by taking L.C.M.
Step 2: Calculate the New Profit-Sharing Ratio of the remaining partners by simply striking off the share of the retiring partner.
Illustration 1:
Ram, Mohan, and Shyam were partners, sharing profits and losses in the ratio of 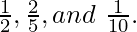 Calculate the New Profit-Sharing Ratio of the remaining Partners if Ram retires.
Calculate the New Profit-Sharing Ratio of the remaining Partners if Ram retires.
Solution:
Step 1: Convert the old profit-sharing ratio into the simplest form by taking L.C.M
The given ratios of 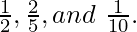 can be written as
can be written as 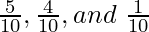 by taking 10 as L.C.M.
by taking 10 as L.C.M.
Step 2: Calculate the New Profit-Sharing Ratio of the remaining partners by simply, striking off the share of the retiring partner.
When Ram retires, then the New Profit-Sharing Ratio between Mohan and Shyam will be 4:1.
Illustration 2:
Riya, Ravi, and Shymali were partners sharing profit and losses in the ratio of 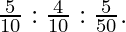 Calculate the New Profit-Sharing Ratio of the remaining Partners if Ravi retires.
Calculate the New Profit-Sharing Ratio of the remaining Partners if Ravi retires.
Solution:
Step 1: Convert the old profit-sharing ratio into the simplest form.
The given ratios of 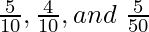 can be written as
can be written as 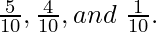
Step 2: Calculate the New Profit-Sharing Ratio of the remaining partners by simply, striking off the share of the retiring partner.
When Ravi retires, then the New Profit-Sharing Ratio between Mohan and Shyam will be 5: 1.
Case 2: When the remaining partner acquires a share of the retiring partner in a certain ratio:
The Remaining Partners may agree to acquire the share of the Retiring Partner in a certain specific ratio. Under such circumstances, the share acquired by the remaining partners is added to their existing shares to determine the new share of the remaining partners.
Steps to determine the New Profit-Sharing Ratio:
Step 1: Calculate the share acquired by the remaining Partners
Divide the share of the retiring partner in the ratio of acquisition agreed upon by the remaining partners.
Step 2: Calculation of New Profit-Sharing Ratio
To find the New Share, add the share acquired by the remaining partners to their old shares.
New Share = Old Share + Share Acquired
Illustration 1 (When a share is acquired by all the remaining partners):
P, Q, and R are partners sharing profits in the ratio of 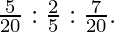 If P retires and his share is taken up by Q and R in the ratio of 1:2. Calculate the New Ratio.
If P retires and his share is taken up by Q and R in the ratio of 1:2. Calculate the New Ratio.
Solution:
Step 1: Calculate the share acquired by the remaining Partners
Share taken by Q from P’s share = 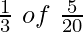 i.e.,
i.e., 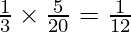
Share taken by R from P’s share = 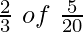 i.e.,
i.e., 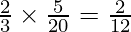
Step 2: Calculation of New Profit-Sharing Ratio
New Share of Q = 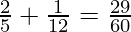
New Share of R = 
New Ratio of Q: R = 29: 31.
Illustration 2 (When a share is acquired by one of the remaining partners):
X, Y, and Z were partners sharing profits in the ratio of 4: 4: 2. Y retires, and his share is taken by Z only. Calculate the New Profit Sharing ratio. (When a share is acquired by one of the remaining partners)
Solution:
Step 1: Calculate the share acquired by the remaining Partners
Share taken by Z from Y’s share = 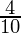
Step 2: Calculation of New Profit-Sharing Ratio
X’s share remains unaffected = 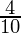
Z’s share = 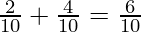
New Ratio of X: Z = 4: 6 i.e., 2: 3.
Share your thoughts in the comments
Please Login to comment...