Class 9 NCERT Solutions- Chapter 10 Circles – Exercise 10.6
Last Updated :
25 Jan, 2021
Question 1. Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
Solution:
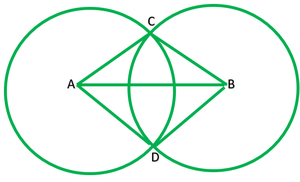
Given: Two circles with Centre A and B circle intersects at C and D.
To prove: ∠ACB=∠ADB
Construction: Join AD,BC and BD
Proof: In ∆ACB and ∆ADB
AC=AD ——–[radii of the same circle]
BC=BD ———[radii of the same circle]
AB=AB ——–[common]
∴∆ACB≅∆ADB ——— [by S.S.S]
∠ACB=∠ADB ——–[c.p.c.t.]
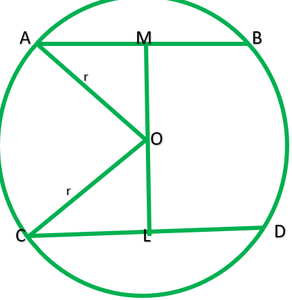
Question 2. Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
Solution:
Let O be the centre of circle and be r cm
Given: AB=5cm, CD =11cm
Construction: Draw OM perpendicular AB and OL perpendicular CD.
Because OM perpendicular AB and OL perpendicular CD and AB||CD.
∴Points O,L, and M are collinear, than ∠M=6cm
Let OL=x
Then OM=6=x
Join AO and CO
OA=OC =r
OL=1/2CD=1/2*11=5.5cm —–[perpendicular from bisects the chord]
AM=1/2AB=1/2*5=2.3cm —–[perpendicular from bisects the chord]
Now, In right ∆DLC
r2=(OL)2+(CL)2
r2=x2+(5.5)2
r2=x2+30.25 ———–1
Now in right ∆OMA
r2=(OM)2+(MA)2
r2=(6-x)2+(2.5)2
r2=36+x2=12x+6.25
r2=x2-12x+42.25 ———–2
Now equating equation 1 and 2
X2+30.25=x2-12x+30.25
12x=42.25-30.25
X=12/12=1
Putting value of x in equation 1
r2=x2+30.25
r2=(1)2+30.25
r2=31.25
r=√31.25=5.6 (approx.)
Radius of circle is 5.6cm.
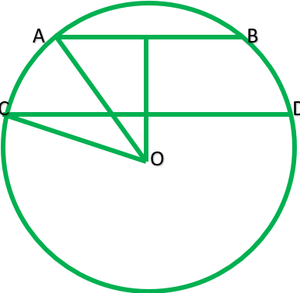
Question 3. The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the center, what is the distance of the other chord from the centre?
Solution:
Let AB and CD are|| chord of circle with centre O which AB=6cm and CD=8cm and radius of circle =r cm.
Construction: Draw OP perpendicular AB and OM perpendicular CD.
Because AB||CD and OP perpendicular AB and OM perpendicular CD therefore. Point O, M and P are collinear.
Clearly, OP=4cm ———-[According to question]
OM=to find?
P is midpoint of AB.
∴AP=1/2 AB=1/2*6=3cm
M is midpoint of AB.
CM=1/2 CD=1/2*8cm=4cm
Join AO and CO
Now in Right ∆OPA,
r2=AP2+PO2
r2=32+42
r2=9+16=25
Now in ∆OMC
r2=CM2+MO2
25=42+MO2
25-16=MO2
9=MO2
√9=MO
3=MO
∴Therefore distance of the other chord from the centre is 3cm
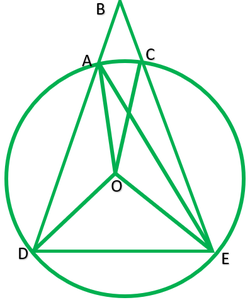
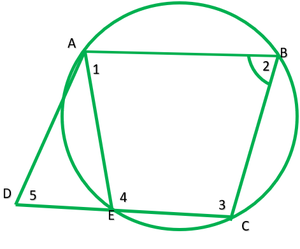
Question 4. Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
Solution:
Give: Vertex B of ∆ABC lie outside the circle,chord AD=CE
To prove: ∠ABC=1/2(∠DOE-∠AOC)
Construction: Join AE
Solution: Chord DE subtends ∠DOE at the center and ∠DAE at point A on the circle.
∴∠DAE=1/2∠DOE ———-1
chords AC subtends ∠AOC at the centre and ∠AEC at point
∴∠AEC=1/2∠AOC ———2
In ∆ ABE,∠DAE is exterior angle
∠DAE=∠ABC +∠AEC
1/2∠DOE=∠ABC+1/2∠AOC
½(∠DOE-∠AOC)= ∠ABC
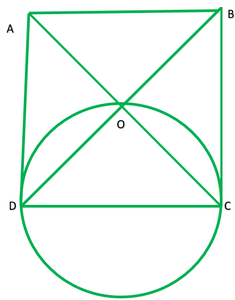
Question 5. Prove that the circle drawn with any side of a rhombus as diameter, passes through the point of intersection of its diagonals.
Solution:
Given: A rhombus ABCD in which O is intersecting point of diagonals AC and BD.
A circle is drawn taking CD as diameter.
To prove: circle points through O or Lies on the circles.
Proof: In rhombus ABCD,
∠DOA=90° ——–[diagonals of rhombus intersect at 90°] 1
In circle:
∠COD=90° ——–[angle made in segment O is right angle] 2
From 1 and 2
O lies on the circle.
Question 6. ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
Solution:
ABCD is a ||gm. The circle through A,B and C intersect at E.
To prove: AE=AD
Proof: Here ABCE is a cyclic quadrilateral
∠2+∠4=180° —–[sum of opposite is of a cyclic quadrilateral is 180°]
∠4=180°-∠1 ——-1
Now ∠4+∠6=180°-∠6 ———2
From 1 and 2
180°-∠2=∠180°-∠6
∠2=∠6 ———–3
Also ∠2=∠5 ———[opposite angles of ||gm are equal] —–4
From 3 and 4
∠5=∠6
Now, In ∆ADE,
∠5=∠6
∴AE=AD ——[sides apposite to equal angles in a∆ are equal]
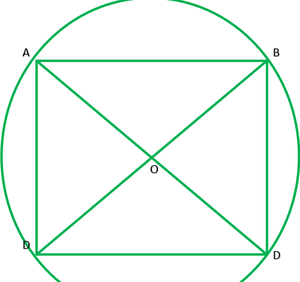
Question 7. AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters, (ii) ABCD is a rectangle.
Solution:
Given: Two chords AC and BD bisects each other i.e OA=OC,OB=OD
To prove: In ∆AOB and COB
AO=CO ——-[given]
∠AOB=∠COD ——[vertically opposite angle]
OB=OD ——–[give]
∴∆AOB≅∆COB ——[s.s.s]
AB=CD ——[C.P.C.T.] 1
similarly ∆AOD≅∆COB (S.A.S)
AD=CD (C.P.C.T.) 2
From 1 and 2 ABCD is a ||gm
Since, ABCD is cyclic quadrilateral
∴∠A+∠C=180°
∠B+∠B=180°
2∠B=180°
∠B=180°/2
∠B=90°
∴ ∠A and ∠B lies in a semicircle
→ AC and BD are diameter of circle.
ii) Since ABCD is a ||gm and ∠A=90°
∴ ABCD is a rectangle.
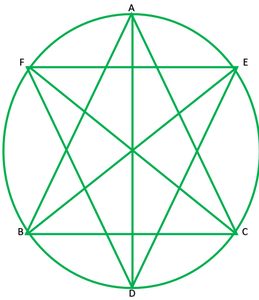
Question 8. Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are 90° – 1 2 A, 90° – 1 2 B and 90° – 1 2 C.
Solution:
Given:∆ABC and it circum-circle AD,BE and CF are bisectors of ∠A,∠B and ∠C
Respectively.
To proof:∠ D=90°-1/2∠A , ∠E=90°-1/2∠B , ∠F=90°-1/2∠C
Construction: Join AE and AF.
Solution: ∠ADE=∠ABE ———-1 [angle in the same segment are equal]
∠ADF=∠ACF ———–2 [angle in the same segment are equal]
Adding 1 and 2
∠ADE+∠ABF=∠ABE+∠ACF
∠D=1/2∠B+1/2∠C ——[BC and CF are bisector of ∠B & ∠c]
∠D=1/2(∠B+∠C)
∠D=1/2(180°-∠A)
∠D=1/2(180°-∠A)
∠D=90°-1/2∠AC
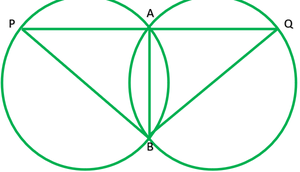
Question 9. Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
Solution:
Given: two congruent circles which intersect at A and B.
PAB is a line segment
To prove: BA=BQ
Construction: join AB
Proof: AB is a common chord of both the congruent circle.
Segment of both circles will be equal
∠P=∠Q
Now, in ∆ BPQ,
∠P=∠Q
BP=BQ ——[sides opposite to equal angles are equal]
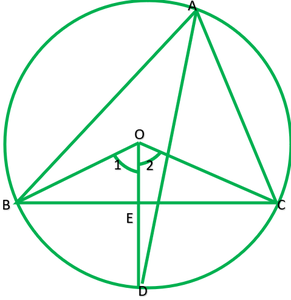
Question 10. In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
Solution:
Given: A ∆ABC, in which AD is angle bisector of ∠A and OD is ⊥ bisector of BC.
To prove: D lies on circumcircle.
Construction: Join OB and OC
Proof: Since BC subtends ∠BAC at A on the remaining of the circle.
∠BOC=2∠BAC ——-1
Now, In ∆BOE and ∆ COE
BO=OE ——–(radii of the same circle)
BE=CE —–(give)
∴∆BOE≅COE ——-(S.S.S)
∠1=∠2 ——-(c.p.c.t)
Now,
∠1+∠2=∠BOC
2∠1=∠BOC
2∠1=2∠BAC ———- (from 1)
∠1=∠BAC
∠BOE=∠BAF
∠BOD=∠BAC
∠BOD=2∠BAD [AD is bisector of ∠BAC]
This is possible only if BD is chord of the circle.
D lies on the circle.
Share your thoughts in the comments
Please Login to comment...