Question 1. Find the discriminant of the following quadratic equations:
(i) 2x2 – 5x + 3 = 0
Solution:
Given quadratic equation: 2x2 – 5x + 3 = 0 ….(1)
As we know that the general form of quadratic equation is
ax2 + bx + c = 0 ….(2)
On comparing eq(1) and (2), we get
Here, a = 2, b = -5 and c = 3
Now, we find the discriminant(D) = b2 – 4ac
D = (-5)2 – 4(2)(3)
= 25 – 24
= 1
Hence, the discriminant of given quadratic equation is 1
(ii) x2 + 2x + 4 = 0
Solution:
Given quadratic equation: x2 + 2x + 4 = 0 ….(1)
As we know that the general form of quadratic equation is
ax2 + bx + c = 0 ….(2)
On comparing eq(1) and (2), we get
Here, a = 1, b = 2 and c = 4
Now, we find the discriminant(D) = b2 – 4ac
D = (2)2 – 4(1)(4)
= 4 – 16
= -12
Hence, the discriminant of given quadratic equation is -12
(iii) (x – 1) (2x – 1)
Solution:
Given quadratic equation:(x – 1)(2x – 1)
Or we can also write as, 2x2 – 3x + 1 = 0 ….(1)
As we know that the general form of quadratic equation is
ax2 + bx + c = 0 ….(2)
On comparing eq(1) and (2), we get
Here, a = 2, b = -3 and c = 1
Now, we find the discriminant(D) = b2 – 4ac
D = (-3)2 – 4(2)(1)
= 9 – 8
= 1
Hence, the discriminant of given quadratic equation is 1
(iv) x2 – 2x + k = 0
Solution:
Given quadratic equation: x2 – 2x + k = 0 ….(1)
As we know that the general form of quadratic equation is
ax2 + bx + c = 0 ….(2)
On comparing eq(1) and (2), we get
Here, a = 1, b = -2 and c = k
Now, we find the discriminant(D) = b2 – 4ac
D = (-2)2 – 4(1)(k)
= 4 -4k
Hence, the discriminant of given quadratic equation is 4 – 4k
(v) √3x2 + 2√2x – 2√3 = 0
Solution:
Given quadratic equation:√3x2 + 2√2x – 2√3 = 0 ….(1)
As we know that the general form of quadratic equation is
ax2 + bx + c = 0 ….(2)
On comparing eq(1) and (2), we get
Here, a =√3, b = 2√2, and c = -2 – 2√3
Now, we find the discriminant(D) = b2 – 4ac
D = (2√2)2 – 4√3(-2√3)
= 8 + 24
= 32
Hence, the discriminant of given quadratic equation is 32
(vi) x2 – x + 1 = 0
Solution:
Given quadratic equation: x2 – x + 1 = 0 ….(1)
As we know that the general form of quadratic equation is
ax2 + bx + c = 0 ….(2)
On comparing eq(1) and (2), we get
Here, a = 1, b = -1 and c = 1
Now, we find the discriminant(D) = b2 – 4ac
D = (-1)2 – 4(1)(1)
= 1 – 4
= -3
Hence, the discriminant of given quadratic equation is -3
Question 2. In the following, determine whether the given quadratic equation have real roots and If so, find the roots:
(i) 16x2 = 24x + 1
Solution:
Given quadratic equation: 16x2 – 24x – 1 = 0 ….(1)
As we know that the general form of quadratic equation is
ax2 + bx + c = 0 ….(2)
On comparing eq(1) and (2), we get
Here, a = 16, b = -24, and c = -1
Now, we find the discriminant(D) = b2 – 4ac
D = (-24)2 – 4(16)(-1)
= 576 + 64
= 640
As we know that for a quadratic equation having real root must satisfy the D >= 0
Here, our equation satisfies the given condition, so it has real roots.
Now we find the real roots using the given formula:
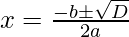
Put the values of b, D, a in the given formula, we get
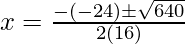
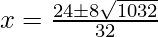
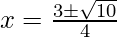
Hence, the value of x is
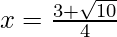
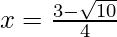
(ii) x2 + x + 2 = 0
Solution:
Given quadratic equation: x2 + x + 2 = 0 ….(1)
As we know that the general form of quadratic equation is
ax2 + bx + c = 0 ….(2)
On comparing eq(1) and (2), we get
Here, a = 1, b = 1 and c = 2
Now, we find the discriminant(D) = b2 – 4ac
D = (1)2 – 4(1)(2)
= 1 – 8
= -7
As we know that for a quadratic equation having real root must satisfy the D >= 0
Here, our equation does not satisfies the given condition, so it does not have real roots.
(iii) √3x2 + 10x – 8√3 = 0
Solution:
Given quadratic equation: √3x2 + 10x – 8√3 = 0 ….(1)
As we know that the general form of quadratic equation is
ax2 + bx + c = 0 ….(2)
On comparing eq(1) and (2), we get
Here, a = √3, b = 10 and c = -8√3
Now, we find the discriminant(D) = b2 – 4ac
D = (10)2 – 4(√3)(-8√3)
= 100 + 96
= 196
As we know that for a quadratic equation having real root must satisfy the D >= 0
Here, our equation satisfies the given condition, so it has real roots.
Now we find the real roots using the given formula:
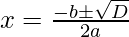
Put the values of b, D, a in the given formula, we get
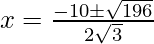
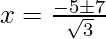
Hence, the value of x is
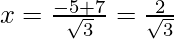
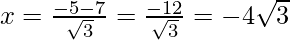
(iv) 3x2 – 2x + 2 = 0
Solution:
Given quadratic equation: 3x2 – 2x + 2 = 0 ….(1)
As we know that the general form of quadratic equation is
ax2 + bx + c = 0 ….(2)
On comparing eq(1) and (2), we get
Here, a = 3, b = -2 and c = 2
Now, we find the discriminant(D) = b2 – 4ac
D = (-2)2 – 4(3)(2)
= 4 – 24
= -20
As we know that for a quadratic equation having real root must satisfy the D >= 0
Here, our equation does not satisfy the given condition, so it does not have real roots.
(v) 2x2 – 2√6x + 3 = 0
Solution:
Given quadratic equation: 2x2 – 2√6x + 3 = 0 ….(1)
As we know that the general form of quadratic equation is
ax2 + bx + c = 0 ….(2)
On comparing eq(1) and (2), we get
Here, a = 2, b= -2√6 and c = 3
Now, we find the discriminant(D) = b2 – 4ac
D = (-2√6)2 – 4(2)(3)
= 24 – 24
= 0
As we know that for a quadratic equation having real root must satisfy the D >= 0
Here, our equation satisfies the given condition, so it has real roots.
Now we find the real roots using the given formula:
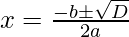
Put the values of b, D, a in the given formula, we get
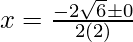
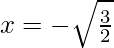
(vi) 3a2x2 + 8abx + 4b2 = 0
Solution:
Given quadratic equation: 3a2x2 + 8abx + 4b2 = 0 ….(1)
As we know that the general form of quadratic equation is
ax2 + bx + c = 0 ….(2)
On comparing eq(1) and (2), we get
Here, a = 3a2, b = 8ab and c = 4b2
Now, we find the discriminant(D) = b2 – 4ac
D = (8ab)2 – 4(3a2)(4b2)
= 64a2b2 – 48a2b2
= 16a2b2
As we know that for a quadratic equation having real root must satisfy the D >= 0
Here, our equation satisfies the given condition, so it has real roots.
Now we find the real roots using the given formula:
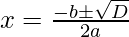
Put the values of b, D, a in the given formula, we get
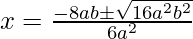
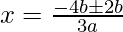
Hence, the value of x is
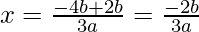
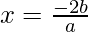
(vii) 3x2 – 2√5x – 5 = 0
Solution:
Given quadratic equation: 3x2 – 2√5x – 5 = 0 ….(1)
As we know that the general form of quadratic equation is
ax2 + bx + c = 0 ….(2)
On comparing eq(1) and (2), we get
Here, a = 3, b = 2√5 and c = -5
Now, we find the discriminant(D) = b2 – 4ac
D = (2√5 )2 – 4(3)(-5)
= 20 + 60
= 80
As we know that for a quadratic equation having real root must satisfy the D >= 0
Here, our equation satisfies the given condition, so it has real roots.
Now we find the real roots using the given formula:
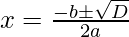
Put the values of b, D, a in the given formula, we get
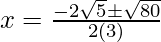
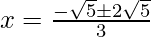
Hence, the value of x is
x = √5 /3
x = -√5
(viii) x2 – 2x + 1 = 0
Solution:
Given quadratic equation: x2 – 2x + 1 = 0 ….(1)
As we know that the general form of quadratic equation is
ax2 + bx + c = 0 ….(2)
On comparing eq(1) and (2), we get
Here, a = 1, b = -2 and c = 1
Now, we find the discriminant(D) = b2 – 4ac
D = (-2)2 – 4(1)(1)
= 4 – 4
= 0
As we know that for a quadratic equation having real root must satisfy the D >= 0
Here, our equation satisfies the given condition, so it has real roots.
Now we find the real roots using the given formula:
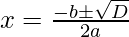
Put the values of b, D, a in the given formula, we get
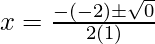
x = 1
(ix) 2x2 + 5√3x + 6 = 0
Solution:
Given quadratic equation: 2x2 + 5√3x + 6 = 0 ….(1)
As we know that the general form of quadratic equation is
ax2 + bx + c = 0 ….(2)
On comparing eq(1) and (2), we get
Here, a = 2, b = 5√3, and c = 6
Now, we find the discriminant(D) = b2 – 4ac
D = (5√3)2 – 4(2)(6)
= 75 – 48
= 27
As we know that for a quadratic equation having real root must satisfy the D >= 0
Here, our equation satisfies the given condition, so it has real roots.
Now we find the real roots using the given formula:
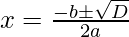
Put the values of b, D, a in the given formula, we get
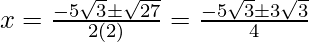
Hence, the value of x is
x = -√3 /2
x = -2√3
(x) √2x2 + 7x + 5√2 = 0
Solution:
Given quadratic equation: √2x2 + 7x + 5√2 = 0 ….(1)
As we know that the general form of quadratic equation is
ax2 + bx + c = 0 ….(2)
On comparing eq(1) and (2), we get
Here, a = √2, b = 7 and c = 5√2
Now, we find the discriminant(D) = b2 – 4ac
D = (7)2 – 4(√2)(5√2)
= 49 – 40
= 9
As we know that for a quadratic equation having real root must satisfy the D >= 0
Here, our equation satisfies the given condition, so it has real roots.
Now we find the real roots using the given formula:
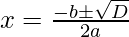
Put the values of b, D, a in the given formula, we get
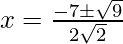
Hence, the value of x is
x = -√2
x = -5/√2
(xi) 2x2 – 2√2x + 1 = 0
Solution:
Given quadratic equation: 2x2 – 2√2x + 1 = 0 ….(1)
As we know that the general form of quadratic equation is
ax2 + bx + c = 0 ….(2)
On comparing eq(1) and (2), we get
Here, a = 2, b = -2√2 and c = 1
Now, we find the discriminant(D) = b2 – 4ac
D = (-2√2)2 – 4(2)(1)
= 8 – 8
= 0
As we know that for a quadratic equation having real root must satisfy the D >= 0
Here, our equation satisfies the given condition, so it has real roots.
Now we find the real roots using the given formula:
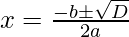
Put the values of b, D, a in the given formula, we get
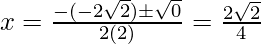
Hence, the value of x is
x = 1/√2
(xii) 3x2 – 5x + 2 = 0
Solution:
Given quadratic equation: 3x2 – 5x + 2 = 0 ….(1)
As we know that the general form of quadratic equation is
ax2 + bx + c = 0 ….(2)
On comparing eq(1) and (2), we get
Here, a = 3, b = -5 and c = 2
Now, we find the discriminant(D) = b2 – 4ac
D = (-5)2 – 4(3)(2)
= 25 – 24
= 1
As we know that for a quadratic equation having real root must satisfy the D >= 0
Here, our equation satisfies the given condition, so it has real roots.
Now we find the real roots using the given formula:
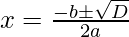
Put the values of b, D, a in the given formula, we get
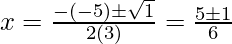
Hence, the value of x is
x = 1
x = 2/3
Question 3. Solve for x:
(i) 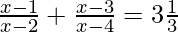 , x ≠ 2, 4
, x ≠ 2, 4
Solution:
Given: 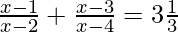
We can also write as
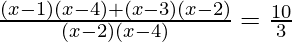
6x2 – 30x + 30 = 10x2 – 60x + 80
4x2 – 30x + 50 = 0
2x2 – 15x + 25 = 0 …(1)
As we know that the general form of quadratic equation is
ax2 + bx + c = 0 ….(2)
On comparing eq(1) and (2), we get
Here, a = 2, b = -15 and c = 25
Now, we find the discriminant(D) = b2 – 4ac
D = (-15)2 – 4(2)(25)
= 225 – 200
= 25
As we know that for a quadratic equation having real root must satisfy the D >= 0
Here, our equation satisfies the given condition, so it has real roots.
Now we find the real roots using the given formula:
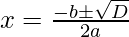
Put the values of b, D, a in the given formula, we get
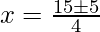
Hence, the value of x is
x = 5
x = 5/2
(ii) x + 1/x = 3, x ≠ 0
Solution:
Given: x + 1/x = 3
We can also write as
x2 – 3x + 1 = 0 …(1)
As we know that the general form of quadratic equation is
ax2 + bx + c = 0 ….(2)
On comparing eq(1) and (2), we get
Here, a = 1, b = -3 and c = 1
Now, we find the discriminant(D) = b2 – 4ac
D = (-3)2 – 4(1)(1)
= 9 – 4
= 5
As we know that for a quadratic equation having real root must satisfy the D >= 0
Here, our equation satisfies the given condition, so it has real roots.
Now we find the real roots using the given formula:
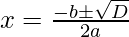
Put the values of b, D, a in the given formula, we get
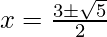
Hence, the value of x is
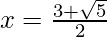
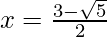
(iii) 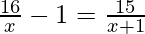 , x ≠ 0, -1
, x ≠ 0, -1
Solution:
Given: 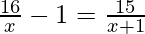
We can also write as
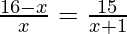
(16 – x)(x + 1) = 15x
15x + 16 – x2 – 15x = 0
16 – x2 = 0
x2 – 16 = 0 ……(1)
As we know that the general form of quadratic equation is
ax2 + bx + c = 0 ….(2)
On comparing eq(1) and (2), we get
Here, a = 1, b = 0, and c = -16
Now, we find the discriminant(D) = b2 – 4ac
D = (0)2 – 4(1)(-16)
= 64
As we know that for a quadratic equation having real root must satisfy the D >= 0
Here, our equation satisfies the given condition, so it has real roots.
Now we find the real roots using the given formula:
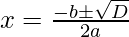
Put the values of b, D, a in the given formula, we get
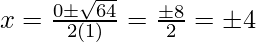
Hence, the value of x is
x = ±4
(iv) 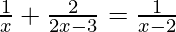 , x ≠ 0, 3/2, 2
, x ≠ 0, 3/2, 2
Solution:
Given: 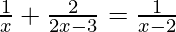
We can also write as
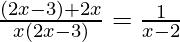
(x – 2)(4x – 3) = x(2x – 3)
x2 – 4x + 3 = 0 ……(1)
As we know that the general form of quadratic equation is
ax2 + bx + c = 0 ….(2)
On comparing eq(1) and (2), we get
Here, a = 1, b = -4, and c = 3
Now, we find the discriminant(D) = b2 – 4ac
D = (-4)2 – 4(1)(3)
= 4
As we know that for a quadratic equation having real root must satisfy the D >= 0
Here, our equation satisfies the given condition, so it has real roots.
Now we find the real roots using the given formula:
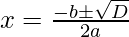
Put the values of b, D, a in the given formula, we get
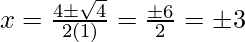
Hence, the value of x is
x = ±3
(v) 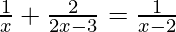 , x ≠ 3, -5
, x ≠ 3, -5
Solution:
Given: 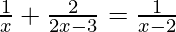
We can also write as
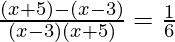
(x – 3)(x + 5) = 6 x 8
x2 + 2x – 63 = 0 ……(1)
As we know that the general form of quadratic equation is
ax2 + bx + c = 0 ….(2)
On comparing eq(1) and (2), we get
Here, a = 1, b = 2, and c = -63
Now, we find the discriminant(D) = b2 – 4ac
D = (2)2 – 4(1)(-63)
= 256
As we know that for a quadratic equation having real root must satisfy the D >= 0
Here, our equation satisfies the given condition, so it has real roots.
Now we find the real roots using the given formula:
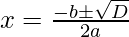
Put the values of b, D, a in the given formula, we get
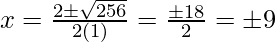
Hence, the value of x is
x = ±9
Share your thoughts in the comments
Please Login to comment...