Class 10 RD Sharma Solutions – Chapter 8 Quadratic Equations – Exercise 8.13

Question 1. A piece of cloth costs ₹ 35. If the piece were 4 m longer and each meter costs ₹ 1 less, the cost would remain unchanged. How long is the piece?

Solution:

Let us considered the length of piece of cloth = x m

Given: The total cost = ₹ 35

So, the cost of 1 m cloth = ₹ 35/x

According to the question,

(x + 4)(35/x – 1) = 35

⇒ 35 – x + (140/x) – 4 = 35

⇒ -x + (140/x) + 31 – 35 = 0

⇒  -x + (140/x) – 4 = 0

⇒ -x² + 140 – 4x = 0

⇒ x² + 4x – 140 = 0

⇒ x² + 14x – 10x – 140 = 0

⇒ x (x + 14) -10 (x + 14) = 0

⇒ (x + 14) (x – 10) = 0

x = 10 or x = -14

Here the value of x = -14 is negative which is not possible

So, the length of piece of cloth = 10 m.

Question 2. Some students planned a picnic. The budget for food was ₹ 480. But eight of these failed to go and thus the cost of food for each member increased by ₹ 10. How many students attended the picnic?

Solution:

Let us considered the number of students = x

Given: The total budget = ₹ 480

So, the share of each student = ₹ 480/x

According to the question,

(480/x – 8) – (480/x) = 10

⇒ 

⇒ 

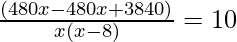
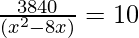
⇒ 10x² – 80x – 3840 = 0

⇒ x² – 8x – 384 = 0               

⇒ x² + 16x – 24x – 384 = 0

⇒ x (x + 16) – 24 (x + 16) = 0

⇒ (x + 16) (x – 24) = 0

x = 24, or x = -16

Here the value of x = -16 is negative which is not possible

So, the number of students = 24.

The total number of students attend the picnic = 24 – 8 = 16

Question 3. A dealer sells an article for ₹ 24 and gains as much percent as the cost price of the article. Find the cost price of the article.

Solution:

Let cost price of the article = ₹ x

Selling price = ₹ 24

Gain = x %

According to the Question,

S.P.= C.P. × (100 + Gain%)/100

24 = x(100 + x)/100

⇒ 2400 = 100x + x²

⇒ x² + 100x – 2400 = 0

⇒ x² – 20x +120x – 2400 = 0

⇒ x(x – 20) + 120(x – 20) = 0

⇒ (x – 20)(x + 120) = 0

x = 20 or x = -120

Here the value of x = -120 is negative which is not possible

Therefore, the cost price of the article = ₹20

Question 4. Out of a group of swans, 7/2 times the square root of the total number are playing on the share of a pond. The two remaining ones are swinging in water. Find the total number of swans.

Solution:

Let us considered the total number of swans = x

According to the question,

7/2(√x) + 2 = x

⇒ 7√x = 2x – 4

On squaring both sides, we get

⇒ 49x = 4x + 16 – 16x

⇒ 4x² – 65x + 16 = 0

⇒ 4x² – 64x – x + 16 = 0 

⇒ 4x(x – 16) – (x – 16) = 0

⇒ (4x – 1)(x – 16) = 0

⇒ x =1/4 or x = 16

Since, number of swans is a natural number we can neglect the solution of a = 1/4

Hence, the total number of swans is 16.

Question 5. If the list price of a toy is reduced by ₹ 2, a person can buy 2 toys mope for ₹ 360. Find the original price of the toy. 

Solution:

Let the original price of the toy = x

The number of toys he can buy at the original price for ₹ 360 = 360/x

According to the question,

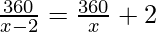
⇒ 360x = (x – 2)(360 + 2x)

⇒ 360x = 360x + 2x² – 720 – 4x

⇒ x² – 2x – 360 = 0

⇒ x² – 20x + 18x – 360 = 0 

⇒ x(x – 20) + 18(x – 20) = 0

⇒ (x + 18)(x – 20) = 0

⇒ x + 18 = 0 or x – 20 = 0

⇒ x = -18 or x = 20

As, the price can’t be negative, x = -18 is neglected.

Thus, the original price of the toy is ₹ 20.

Question 6. ₹ 9000 were divided equally among a certain number of persons. Had there been 20 more persons, each would have got ₹ 160 less. Find the original number of persons.

Solution:

Let’s consider the original number of people = a

Amount which each receives when a person are present = 9000/a

According to the question,

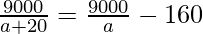
⇒ 9000a = (9000 – 160a)(a + 20)

⇒ 9000a = 9000a + 180000 – 160a² – 3200a

⇒ a² + 20a – 1125 = 0

⇒ a² + 45a – 25a – 1125 = 0

⇒ a(a + 45) – 25(a + 45) = 0

⇒ (a – 25)(a + 45) = 0

⇒ a = 25 or a = -45 (Number of people can never be negative,

                                   so we can neglect this value)

Therefore, the original number of people = 25.

Question 7. Some students planned a picnic. The budget for food was ₹ 500. But 5 of them failed to go and thus the cost of food for each number increased by ₹ 5. How many students attended the picnic? 

Solution:

Let us considered the number of students = x

Given: The total budget = ₹ 500

So, the share of each student = ₹ 500/x

The number of students failed to go = 5

According to the question,

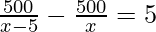
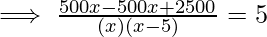
⇒ 5x² – 25x – 2500 = 0

⇒ x² – 5x – 500 = 0                    

⇒ x² – 25x + 20x – 500 = 0

⇒ x(x – 25) + 20(x – 25) = 0

⇒ (x – 25)(x + 20) = 0

⇒ x – 25 = 0 or x + 20 = 0

⇒ x = 25 or x = -20

Here the value of x = -20 is negative which is not possible

So, the number of students = 25

Question 8. A pole has to be erected at a point on the boundary of a. circular park of diameter 13 meters in such a way that the difference, of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 meters. Is it the possible to do so? If yes, at what distances from the two gates Should the pole be erected?

Solution:

In the given circle, AB(Diameter) = 13 m

Let us considered P be the pole in the circle.

So, PB = x m and PA= (x + 7) m

In the triangle APB

AB² = AP² + PB²

⇒ 13² = (x + 7)² + (x)²

⇒ 169 = x² + 49 +14x + x²

⇒ 2x² + 14x -120 = 0

⇒ x² +7x – 60 = 0

⇒ x² +12x – 5x – 60 = 0

⇒ x(x + 12) – 5(x + 12) = 0

⇒ (x + 12)(x – 5) = 0

x = -12 or x = 5

Here the value of x = -12 is negative which is not possible

So the value valid of x = 5

Hence, PB = 5 m and PA = 5 + 7 = 12 m.

Question 9. In a class test, the sum of the marks obtained by P in Mathematics and Science is 28. Had he got 3 marks more in Mathematics and 4 marks less in Science. The product of their marks, would have been 180. Find his marks in the two subjects.

Solution:

Given: The sum of marks obtained by P in Mathematics and Science = 28

So let us considered the marks in Mathematics = x

and the marks in Science = 28 – x

According to the question

(x + 3) (28 – x – 4) = 180

⇒ (x + 3) (24 – x) = 180

⇒ 24x – x² + 72 – 3x = 180

⇒ 21x – x² + 72 – 180 = 0

⇒ – x² + 21x – 108 = 0

⇒ x² – 21x + 108 = 0

⇒ x² – 9x – 12x + 108 = 0

⇒ x (x – 9) – 12 (x – 9) – 0

⇒ (x – 9)(x – 12) = 0

x = 9 or x = 12

So, if we take x = 9 then the marks in 

Mathematics = 9 and marks in Science = 19

So, if we take x = 12 then the marks in 

Mathematics = 12 and marks in English = 16

Question 10. In a class test, the sum of Shefali’s marks in Mathematics and English is 30. Had she got 2 marks more in Mathematics and 3 marks less in English, the product of her marks would have been 210. Find her marks in two subjects. 

Solution:

Given: Sum of Shefali’s marks in Mathematics and English = 30

So let us considered the marks in Mathematics = x

and the marks in English = 30 – x

According to the question

(x + 2) (30 – x – 3) = 210

⇒ (x + 2) (27 – x) = 210

⇒ 27x – x² + 54 – 2x – 210 = 0

⇒ – x² + 25x – 156 = 0

⇒ x² – 25x + 156 = 0

⇒ x² – 12x – 13x +156 = 0

⇒ x (x – 12) – 13 (x – 12) = 0

⇒ (x – 12) (x – 13) = 0

x = 13 or x = 12

So, if we take x = 13 then the marks in 

Mathematics = 12 and marks in English = 18

So, if we take x = 12 then the marks in 

Mathematics = 13 and marks in English = 17

Question 11. A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was ₹ 90, And the number of articles produced and the cost of each article. 

Solution:

Given: Total cost of production on that day = ₹90

So, Let us considered the number of articles = x

Hence the price of each article = 2x + 3

According to the question,

x (2x + 3) = 90

⇒ 2x² + 3x – 90 = 0

⇒ 2x² -12x + 15x – 90 = 0

⇒ 2x (x – 6) + 15 (x – 6) = 0

⇒ (x – 6) (2x + 15) = 0

If x – 6 = 0

So, x = 6

If 2x + 15 = 0

So x = -15/2

Here the value of x is negative which is not possible

So the value valid of x = 6

Hence the number of articles = 6

And price of each article = 2x + 3 = 2 x 6 + 3 = 12 + 3 = 15

Question 12. At t minutes past 2 pm the time needed by the minutes hand and a clock to show 3 pm was found to be 3 minutes less than t²/4 minutes. Find t.

Solution:

As we already know that, the time between 2 pm to 3 pm = 1 h = 60 minutes

Given: At t minutes past 2 pm, the time needed by the minutes hand of a clock 

to show 3 pm was found to be 3 minutes less than t²/4 minutes.

Find: the value of t

So,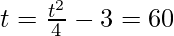 

⇒ 4t + t² – 12 = 240

⇒ t² + 4t – 252 = 0

⇒ t² + 18t – 14t – 252 = 0 

⇒ t (t + 18) – 14 (t + 18) = 0

⇒ (t + 18) (t – 14) = 0 

As we know that time cannot be negative, so t ≠ -18

Hence, t = 14 min