Class 10 RD Sharma Solutions – Chapter 6 Trigonometric Identities – Exercise 6.2
Last Updated :
28 Apr, 2021
Question 1. If cos θ = 4/5, find all other trigonometric ratios of angle θ.
Solution:
We are given, cos θ = 4/5. So, sec θ =1/cos θ = 5/4.
Now we know,
=> sin θ = √(1 – cos2 θ)
=> sin θ = √(1 – (4/5)2)
=> sin θ = √(1 – (16/25))
=> sin θ = √(9/25)
=> sin θ = 3/5
So, cosec θ = 1/sin θ = 5/3
And tan θ = sin θ/cos θ = (3/5)/(4/5) = 3/4
Therefore, cot θ = 1/tan θ = 4/3
If cos θ = 4/5, value of sec θ, sin θ, cosec θ, tan θ and cot θ are 5/4, 3/5, 5/3, 3/4 and 4/3 respectively.
Question 2. If sin θ = 1/√2, find all other trigonometric ratios of angle θ.
Solution:
We are given, sin θ = 1/√2. So, cosec θ =1/sin θ = √2.
Now we know,
=> cos θ = √(1 – sin2 θ)
=> cos θ = √(1 – (1/√2)2)
=> cos θ = √(1 – (1/2))
=> cos θ = √(1/2)
=> cos θ = 1/√2
So, sec θ = 1/cos θ = √2
And tan θ = sin θ/cos θ = (1/√2)/(1/√2) = 1
Therefore, cot θ = 1/tan θ = 1
If sin θ = 1/√2, value of cosec θ, cos θ, sec θ, tan θ and cot θ are √2, 1/√2, √2, 1 and 1 respectively.
Question 3. If tan θ = 1/√2, find the value of 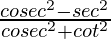 .
.
Solution:
We are given, tan θ = 1/√2. Now we know,
=> sec θ = √(1 + tan2 θ)
=> sec θ = √(1 + (1/√2)2)
=> sec θ = √(1+(1/2))
=> sec θ = √(3/2)
And cot θ = 1/tan θ = √2. Also, we know,
=> cosec θ = √(1 + cot2 θ)
=> cosec θ = √(1 + (√2)2)
=> cosec θ = √(1 + 2)
=> cosec θ = √3
So, 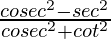 =
= 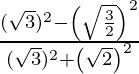
= 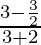
= 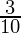
Therefore, the value of 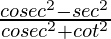 is
is 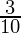 .
.
Question 4. If tan θ = 3/4, find the value of 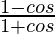 .
.
Solution:
We are given, tan θ = 3/4. Now we know,
=> sec θ = √(1 + tan2 θ)
=> sec θ = √(1 + (3/4)2)
=> sec θ = √(1+(9/16))
=> sec θ = √(25/16)
=> sec θ = 5/4
And cos θ = 1/sec θ = 4/5.
So, 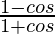 =
= 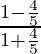
= 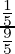
= 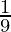
Therefore, the value of 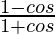 is
is 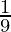 .
.
Question 5. If tan θ = 12/5, find the value of 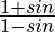 .
.
Solution:
We are given, tan θ = 12/5. So, cot θ = 1/tan θ = 5/12.
Now we know,
=> cosec θ = √(1 + cot2 θ)
=> cosec θ = √(1 + (5/12)2)
=> cosec θ = √(1 + (25/144))
=> cosec θ = √(169/144)
=> cosec θ = 13/12
And sin θ = 1/cosec θ = 12/13.
So, 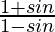 =
= 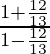
= 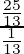
= 25
Therefore, the value of 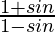 is 25.
is 25.
Question 6. If cot θ = 1/√3, find the value of 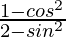 .
.
Solution:
We are given, cot θ = 1/√3. Now we know,
=> cosec θ = √(1 + cot2 θ)
=> cosec θ = √(1 + (1/√3)2)
=> cosec θ = √(1 + (1/3))
=> cosec θ = √(4/3)
=> cosec θ = 2/√3
And sin θ = 1/cosec θ = √3/2. Also, we know,
=> cos θ = √(1 – sin2 θ)
=> cos θ = √(1 – (√3/2)2)
=> cos θ = √(1 – (3/4))
=> cos θ = √(1/4)
=> cos θ = 1/2
So, 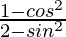 =
= 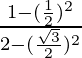
= 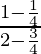
= 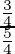
= 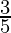
Therefore, the value of 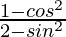 is
is 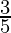 .
.
Question 7. If cosec A = √2, find the value of 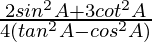 .
.
Solution:
We are given, cosec A = √2. So, sin A = 1/cosec A = 1/√2.
Now we know,
=> cos A = √(1 – sin2 A)
=> cos A = √(1 – (1/√2)2)
=> cos A = √(1 – (1/2))
=> cos A = √(1/2)
=> cos A = 1/√2
Hence, tan A = sin A/cos A = (1/√2)/(1/√2) = 1. And cot A = 1/tan A = 1.
So, 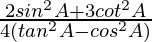 =
= 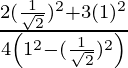
= 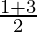
= 2
Therefore, the value of 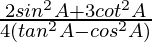 is 2.
is 2.
Question 8. If cot θ = √3, find the value of 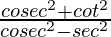 .
.
Solution:
We are given cot θ = √3. And tan θ = 1/cot θ = 1/√3.
Now we know,
=> cosec θ = √(1 + cot2 θ)
=> cosec θ = √(1 + (√3)2)
=> cosec θ = √4
=> cosec θ = 2
Also, we know,
=> sec θ = √(1 + tan2 θ)
=> sec θ = √(1 + (1/√3)2)
=> sec θ = √(1+(1/3))
=> sec θ = √(4/3)
=> sec θ = 2/√3
So, 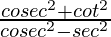 =
= 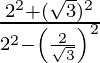
= 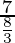
= 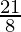
Therefore, the value of 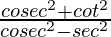 is
is 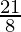 .
.
Question 9. If 3cos θ = 1, find the value of 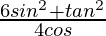 .
.
Solution:
We are given cos θ = 1/3. Now we know,
=> sin θ = √(1 – cos2 θ)
=> sin θ = √(1 – (1/3)2)
=> sin θ = √(1 – (1/9))
=> sin θ = √(8/9)
=> sin θ = 2√2/3
Hence, tan θ = sin θ/cos θ = (2√2/3)/(1/3) = 2√2
So, 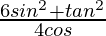 =
= 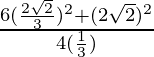
= 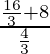
= 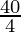
= 10
Therefore, the value of 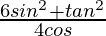 is 10.
is 10.
Question 10. If √3 tan θ = sin θ, find the value of sin2 θ – cos2 θ.
Solution:
We are given, √3 tan θ = sin θ
=> √3 (sin θ/cos θ) = sin θ
=> cos θ = 1/√3
Now we know,
=> sin θ = √(1 – cos2 θ)
=> sin θ = √(1 – (1/√3)2)
=> sin θ = √(1 – (1/3))
=> sin θ = √(2/3)
So, sin2 θ – cos2 θ = √(2/3)2 – (1/√3)2
= 2/3 – 1/3
= 1/3
Therefore, the value of sin2 θ – cos2 θ is 1/3.
Question 11. If cosec θ = 13/12, find the value of 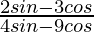 .
.
Solution:
We are given, cosec θ = 13/12. So, sin θ = 1/cosec θ = 12/13.
Now we know,
=> cos θ = √(1 – sin2 θ)
=> cos θ = √(1 – (12/13)2)
=> cos θ = √(1 – (144/169))
=> cos θ = √(25/169)
=> cos θ = 5/13
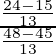
So, 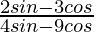 =
= 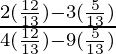
= 
= 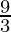
= 3
Therefore, the value of 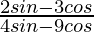 is 3.
is 3.
Question 12. If sin θ + cos θ = √2 cos (90o–θ), find cot θ.
Solution:
We are given,
=> sin θ + cos θ = √2 cos (90o–θ)
=> sin θ + cos θ = √2 sin θ
=> cos θ = (√2–1)sin θ
=> cos θ/sin θ = √2–1
=> cot θ = √2–1
Therefore, value of cot θ is √2–1.
Question 13. If 2sin2 θ – cos2 θ = 2, then find the value of θ.
Solution:
We have,
=> 2sin2 θ – cos2 θ = 2
=> 2sin2 θ – (1 – sin2 θ) = 2
=> 2sin2 θ – 1 + sin2 θ = 2
=> 3sin2 θ = 3
=> sin2 θ = 1
=> sin θ = 1
=> θ = 90o
Therefore, the value of θ is 90o.
Question 14. If √3tan θ – 1 = 0, find the value of sin2 θ – cos2 θ.
Solution:
We are given,
=> √3tan θ – 1 = 0
=> tan θ = 1/√3
=> tan θ = tan 30o
=> θ = 30o
So, sin2 θ – cos2 θ = sin2 30o – cos2 30o
= (1/2)2 – (√3/2)2
= (1/4) – (3/4)
= –2/4
= –1/2
Therefore, the value of sin2 θ – cos2 θ is –1/2.
Share your thoughts in the comments
Please Login to comment...