Prove the following trigonometric identities:
Question 57. tan2 A sec2 B − sec2 A tan2 B = tan2 A − tan2 B
Solution:
We have,
L.H.S. = tan2 A sec2 B − sec2 A tan2 B
= tan2 A (1 + tan2 B) − tan2 B (1+ tan2 A)
= tan2 A + tan2 A tan2 B − tan2 B − tan2 A tan2 B
= tan2A − tan2B
= R.H.S.
Hence proved.
Question 58. If x = a sec θ + b tan θ and y = a tan θ + b sec θ, Prove that x2 − y2 = a2 − b2.
Solution:
We have,
L.H.S. = x2 − y2
= (a sec θ + b tan θ)2 − (a tan θ + b sec θ)2
= a2 sec2 θ + b2 tan2 θ + 2ab sec θ tan θ − a2 tan2 θ − b2 sec2 θ – 2ab sec θ tan θ
= a2 sec2 θ + b2 tan2 θ − a2 tan2 θ − b2 sec2 θ
= a2 sec2 θ − b2 sec2 θ + b2 tan2θ − a2 tan2 θ
= sec2 θ (a2 − b2) + tan2 θ (b2 − a2)
= sec2θ (a2 − b2) − tan2θ (a2 − b2)
= (sec2 θ − tan2θ) (a2 − b2)
= a2 − b2
= R.H.S.
Hence proved.
Question 59. If 3 sin θ + 5 cos θ = 5, prove that 5 sin θ – 3 cos θ = 3.
Solution:
We are given,
=> 3 sin θ + 5 cos θ = 5
=> 3 sin θ = 5 (1 − cos θ)
=> 3 sin θ = 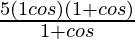
=> 3 sin θ = 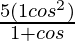
=> 3 sin θ = 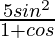
=> 3 (1 + cos θ) = 5 sin θ
=> 3 + 3 cos θ = 5 sin θ
=> 5 sin θ − 3 cos θ = 3
Hence proved.
Question 60. If cosec θ + cot θ = m and cosec θ – cot θ = n, prove that m n = 1.
Solution:
We have,
L.H.S. = m n
= (cosec θ + cot θ) (cosec θ – cot θ)
= cosec2 θ − cot2 θ
= 1
= R.H.S.
Hence proved.
Question 61. If Tn = sinn θ + cosn θ, Prove that 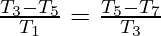 .
.
Solution:
We have,
L.H.S. = 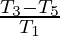
= 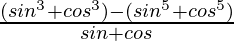
= 
= 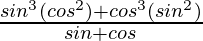
= 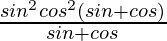
= sin2 θ cos2 θ
And R.H.S. = 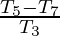
= 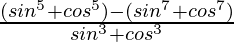
= 
= 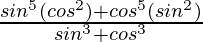
= 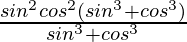
= sin2 θ cos2 θ
Therefore, L.H.S. = R.H.S.
Hence proved.
Question 62. 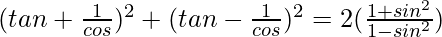
Solution:
We have,
L.H.S. = 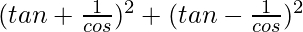
= (tan θ + sec θ)2 + (tan θ – sec θ)2
= tan2θ + sec2θ + 2 tan θ sec θ + tan2 θ + sec2θ – 2 tan θ sec θ
= 2[tan2 θ + sec2 θ]
= 2\frac{sin^2θ}{cos^2θ}+\frac{1}{cos^2θ}
= 2\frac{1+sin^2θ}{cos^2θ}
= 2\frac{1+sin^2θ}{1-sin^2θ}
= R.H.S.
Hence proved.
Question 63. 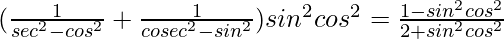
Solution:
We have,
L.H.S. = 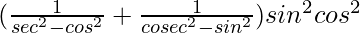
= 
= 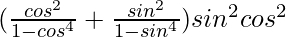
= 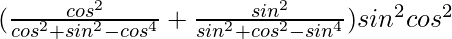
= ![Rendered by QuickLaTeX.com [\frac{cos^2θ}{cos^2θ(1-cos^2θ)+sin^2θ}+\frac{sin^2θ}{sin^2θ(1-sin^2θ)+cos^2θ}]sin^2θcos^2θ](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e339d47a3119ba8dabe7b17489c894c0_l3.png)
= ![Rendered by QuickLaTeX.com [\frac{cos^2θ}{sin^2θ(cos^2θ+1)}+\frac{sin^2θ}{cos^2θ(sin^2θ+1)}]sin^2θcos^2θ](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9a6355fe1ba706be71875e5ab14a85a0_l3.png)
= ![Rendered by QuickLaTeX.com \left[\frac{cos^4θ+cos^4θsin^2θ+sin^4θ+sin^4θcos^2θ}{sin^2θcos^2θ(cos^2θ+1)(sin^2θ+1)}\right]sin^2θcos^2θ](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0d903643e7d0096ca9dc1fd675c28d27_l3.png)
= 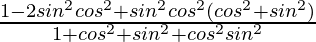
= 
= R.H.S.
Hence proved.
Question 64. (i) ![Rendered by QuickLaTeX.com \left[\frac{1+sinθ-cosθ}{1+sinθ+cosθ}\right]^2=\frac{1-cosθ}{1+cosθ}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8154c89d38ecb1651a08a3c8439114db_l3.png)
Solution:
We have,
L.H.S. = ![Rendered by QuickLaTeX.com \left[\frac{1+sinθ-cosθ}{1+sinθ+cosθ}\right]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-805fe4be149141709f1fe9f284b669bf_l3.png)
= ![Rendered by QuickLaTeX.com \left[\frac{(1+sinθ-cosθ)(1+sinθ-cosθ)}{(1+sinθ+cosθ)(1+sinθ-cosθ)}\right]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-650881268c5c447f3814be9b8ba0e0b7_l3.png)
= ![Rendered by QuickLaTeX.com \left[\frac{(1+sinθ-cosθ)^2}{(1+sinθ)^2-cos^2θ}\right]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-96915190c7e9e065e03afb7735265db5_l3.png)
= ![Rendered by QuickLaTeX.com \left[\frac{1+sin^2θ+cos^2θ+2sinθ-2sinθcosθ-2cosθ}{1+sin^2θ+2sinθ-cos^2θ}\right]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6fc0d7691c1eb2abe3ddc1e8ad451678_l3.png)
= ![Rendered by QuickLaTeX.com \left[\frac{2+2sinθ-2sinθcosθ-2cosθ}{2sin^2θ+2sinθ}\right]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-63d769148d5073cc4d267ff7e2a7e8df_l3.png)
= ![Rendered by QuickLaTeX.com \left[\frac{2(1+sinθ)-2cosθ(sinθ+1)}{2sinθ(sinθ+1)}\right]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2ac61bb23ee7b9e02bc6870f3d3333de_l3.png)
= ![Rendered by QuickLaTeX.com \left[\frac{(1+sinθ)(2-2cosθ)}{2sinθ(sinθ+1)}\right]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-aae6638cc725e0d507ff71703126a949_l3.png)
= ![Rendered by QuickLaTeX.com \left[\frac{2-2cosθ}{2sinθ}\right]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-463a9eed4bc8b715e369b86352ce092a_l3.png)
= 
= 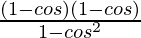
= 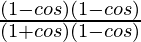
= 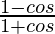
= R.H.S.
Hence proved.
(ii) 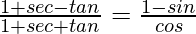
Solution:
We have,
L.H.S. = 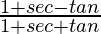
= 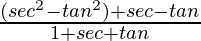
= 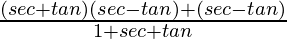
= ![Rendered by QuickLaTeX.com \frac{(secθ-tanθ)[1+secθ+tanθ]}{1+secθ+tanθ}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0c97263dfb0a3592d4b8b6be79363f97_l3.png)
= sec θ − tan θ
= 1/cos θ − sin θ/cos θ
= 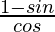
= R.H.S.
Hence proved.
Question 65. (sec A + tan A − 1) (sec A – tan A + 1) = 2 tan A
Solution:
We have,
L.H.S. = (sec A + tan A − 1) (sec A – tan A + 1)
= [sec A + tan A − (sec A + tan A) (sec A – tan A)] [sec A – tan A + (sec A – tan A)(sec A + tan A)]
= (sec A + tan A) (1 − (sec A – tan A)) (sec A – tan A) (1 + (sec A + tan A))
= (sec2 A − tan2 A) (1 – sec A + tan A) (1 + sec A + tan A)
= (1 – sec A + tan A) (1 + sec A + tan A)
= (1 – 1/cos A + sin A/cos A) (1 + 1/cos A + sin A/cos A)
= 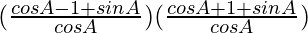
= 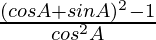
= 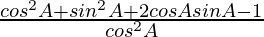
= 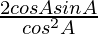
= sin A/cos A
= 2 tan A
= R.H.S.
Hence proved.
Question 66. (1 + cot A − cosec A)(1 + tan A + sec A) = 2
Solution:
We have,
L.H.S. = (1 + cot A − cosec A)(1 + tan A + sec A)
= (1 + cos A/sin A − 1/sin A)(1 + sin A/cos A + 1/cos A)
= 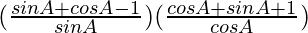
= 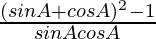
= 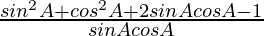
= 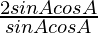
= 2
= R.H.S.
Hence proved.
Question 67. (cosec θ – sec θ) (cot θ – tan θ) = (cosec θ + sec θ) (sec θ cosec θ − 2)
Solution:
We have,
L.H.S. = (cosec θ – sec θ) (cot θ – tan θ)
= ![Rendered by QuickLaTeX.com [\frac{1}{sinθ}-\frac{1}{cosθ}][\frac{cosθ}{sinθ}-\frac{sinθ}{cosθ}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a0860f785949b7206ab45e883e8c23d5_l3.png)
= ![Rendered by QuickLaTeX.com [\frac{cosθ-sinθ}{sinθcosθ}][\frac{cos^2θ-sin^2θ}{sinθcosθ}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c163a9375f8a8bdd2b778dd6bb5346fc_l3.png)
= ![Rendered by QuickLaTeX.com \left[\frac{(cosθ-sinθ)^2(cosθ+sinθ)}{sin^2θcos^2θ}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a951f12627f2070086b6d79abcf3fd47_l3.png)
And R.H.S. = (cosec θ + sec θ) (sec θ cosec θ − 2)
= ![Rendered by QuickLaTeX.com [\frac{1}{sinθ}+\frac{1}{cosθ}][(\frac{1}{cosθ})(\frac{1}{sinθ})-2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b00c342cbcfb4b7168edfb84842e6c65_l3.png)
= ![Rendered by QuickLaTeX.com [\frac{sinθ+cosθ}{sinθcosθ}][\frac{1-2sinθcosθ}{sinθcosθ}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e86d947668fcb01aa0202e97ca3eaa41_l3.png)
= ![Rendered by QuickLaTeX.com [\frac{sinθ+cosθ}{sinθcosθ}][\frac{sin^2θ+cos^2θ-2sinθcosθ}{sinθcosθ}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-aec7a47904a0065e50fae34df7abe84e_l3.png)
= ![Rendered by QuickLaTeX.com [\frac{sinθ+cosθ}{sinθcosθ}][\frac{(sinθ-cosθ)^2}{sinθcosθ}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dd416630abce93e528925ddac6f0b89c_l3.png)
= ![Rendered by QuickLaTeX.com \left[\frac{(cosθ-sinθ)^2(cosθ+sinθ)}{sin^2θcos^2θ}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a951f12627f2070086b6d79abcf3fd47_l3.png)
Therefore, L.H.S. = R.H.S.
Hence proved.
Question 68. 
Solution:
We have,
L.H.S. = 
= 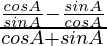
= 
= 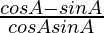
= cosec A − sec A
= R.H.S.
Hence proved.
Question 69. 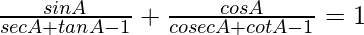
Solution:
We have,
L.H.S. = 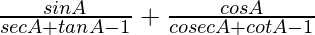
= 
= 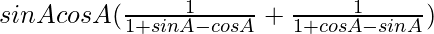
= 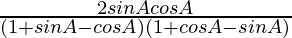
= 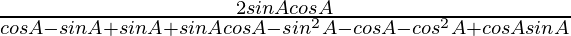
= 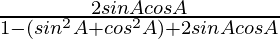
= 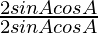
= 1
= R.H.S.
Hence proved.
Question 70. 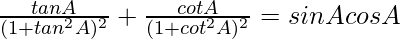
Solution:
We have,
= 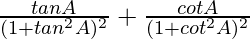
= 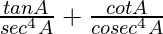
= 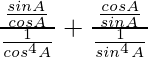
= sin A cos3 A + cos A sin3 A
= sin A cos A (sin2 A + cos2 A)
= sin A cos A
= R.H.S.
Hence proved.
Question 71. sec4 A (1 − sin4 A) – 2 tan2 A = 1
Solution:
We have,
L.H.S. = sec4 A (1 − sin4 A) – 2 tan2 A
= sec4 A – tan4 A – 2 tan4 A
= (sec2 A)2 – tan4 A – 2 tan4 A
= (1+ tan2 A)2 − tan4 A − 2tan4 A
= 1 + tan4 A + 2tan2 A − tan4 A − 2tan4 A
= 1
= R.H.S.
Hence proved.
Question 72. 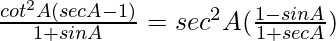
Solution:
We have,
L.H.S. = 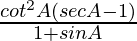
= 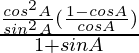
= 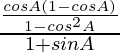
= 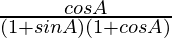
And R.H.S. = 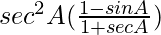
= 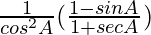
= 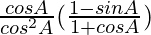
= 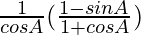
= 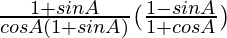
= 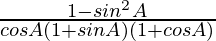
= 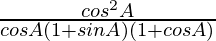
= 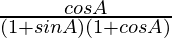
Therefore, L.H.S. = R.H.S.
Hence proved.
Question 73. (1 + cot A + tan A) (sin A – cos A) = sin A tan A – cos A cot A
Solution:
We have,
L.H.S. = (1 + cot A + tan A) (sin A – cos A)
= sin A – cos A + cot A sin A – cot A cos A + sin A tan A – tan A cos A
= sin A – cos A + cos A – cot A cos A + sin A tan A – sin A
= sin A tan A – cos A cot A
= R.H.S
Hence proved.
Question 74. If x cos θ/a + y sin θ/b = 1 and x cos θ/a – y sin θ/b = 1, then prove that x2/a2 + y2/b2 = 2.
Solution:
We have,
x cos θ/a + y sin θ/b = 1 . . . . (1)
x cos θ/a – y sin θ/b = 1 . . . . (2)
On squaring both sides of (1) and (2) and adding them we get,
=> (x cos θ/a + y sin θ/b)2 + (x cos θ/a – y sin θ/b)2 = 1 + 1
=> 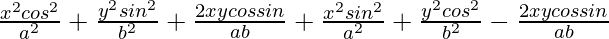 = 2
= 2
=> 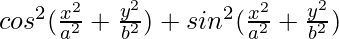 = 2
= 2
=>  = 2
= 2
Hence proved.
Question 75. If cosec θ – sin θ = a3, sec θ – cos θ = b3, Prove that a2b2 (a2+ b2) = 1.
Solution:
We are given,
=> cosec θ – sin θ = a3
=> 1/sin θ – sin θ = a3
=> a3 = 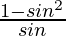
=> a3 = 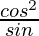
=> a = 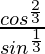
On squaring both sides, we get,
=> a2 = 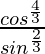
Also we have,
=> sec θ – cos θ = b3
=> 1/cos θ – cos θ = b3
=> b3 = 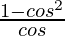
=> b3 = 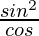
=> b = 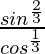
On squaring both sides, we get,
=> b2 = 
So, L.H.S. = a2b2 (a2+ b2)
= 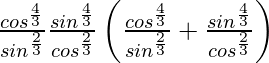
= 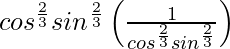
= 1
= R.H.S.
Hence proved.
Question 76. If a cos3 θ + 3a cos θ sin2 θ = m and a sin3 θ + 3a cos2 θ sin θ = n, prove that

Solution:
We are given,
m = a cos3 θ + 3a cos θ sin2 θ and n = a sin3 θ + 3a cos2 θ sin θ
So, L.H.S. = 
= (a cos3 θ + 3a cos θ sin2 θ + a sin3 θ + 3a cos2 θ sin θ)2/3 + (a cos3 θ + 3a cos θ sin2 θ – a sin3 θ – 3a cos2 θ sin θ)2/3
= a2/3 ((cos θ + sin θ)3)2/3 + a2/3 ((cos θ − sin θ)3)2/3
= a2/3 [(cos θ + sin θ)2 + (cos θ − sin θ)2]
= a2/3 [cos2 θ + sin2 θ + 2 sin θ cos θ + cos2 θ + sin2 θ − 2 sin θ cos θ]
= 2 a2/3
= R.H.S.
Hence proved.
Question 77. If x = a cos3 θ, y = b sin3θ, prove that (x/a)2/3 + (y/b)2/3 = 1.
Solution:
Given x = a cos3 θ and y = b sin3 θ.
So, L.H.S. = (x/a)2/3 + (y/b)2/3
= 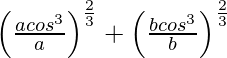
= (cos3 θ)2/3 + (sin3 θ)2/3
= cos2 θ + sin2 θ
= 1
= R.H.S.
Hence proved.
Question 78. If a cos θ + b sin θ = m and a sin θ – b cos θ = n, Prove that a2 + b2 = m2 + n2.
Solution:
We have,
R.H.S = m2 + n2
= (a cos θ + b sin θ)2 + (a sin θ – b cos θ)2
= a2 cos2 θ + b2 sin2θ + 2ab sin θ cos θ + a2 sin2 θ + b2 cos2 θ – 2ab sin θ cos θ
= a2 cos2 θ + a2 cos2 θ + b2 sin2 θ + b2 cos2 θ
= a2 (sin2 θ + cos2 θ) + b2 (sin2 θ + cos2 θ)
= a2 + b2
= L.H.S.
Hence proved.
Question 79. If cos A + cos2 A = 1, Prove that sin2 A + sin4 A = 1.
Solution:
We are given,
=> cos A + cos2 A = 1
=> cos A = 1 − cos2 A
=> cos A = sin2 A . . . . (1)
Now, L.H.S. = sin2 A + sin4 A
Using (1), we get,
= cos A + cos2 A
= 1
= R.H.S.
Hence proved.
Question 80. If cos θ + cos2 θ = 1, prove that sin12 θ + 3 sin10 θ + 3 sin8 θ + sin6 θ + 2 sin4 θ + 2 sin2 θ − 2 = 1.
Solution:
We are given,
=> cos θ + cos2 θ = 1
=> cos θ = 1 − cos2 θ
=> cos θ = sin2 θ . . . . (1)
Now, L.H.S. = sin12 θ + 3 sin10 θ + 3 sin8 θ + sin6 θ + 2 sin4 θ + 2 sin2 θ − 2
= (sin4 θ)3 + 3 sin4 θ sin2 θ (sin4 θ + sin2 θ) + (sin2 θ)3 + 2(sin2 θ)2 + 2 sin2 θ − 2
Using (1), we get,
= (sin4 θ + sin2 θ)3 + 2cos2 θ + 2 cos θ − 2
= ((sin2 θ)2 + sin2 θ)3 + 2 cos2 θ + 2 cos θ – 2
= (cos2 θ + sin2 θ)3 + 2 cos2 θ + 2 cos θ − 2
= 1 + 2(cos2 θ + sin2 θ) − 2
= 1 + 2(1) −2
= 1
= R.H.S.
Hence proved.
Question 81. Given that: (1 + cos α)(1 + cos β)(1 + cos γ) = (1 – cos α)(1 – cos β)(1 – cos γ). Show that one of the values of each member of this equality is sin α sin β sin γ.
Solution:
We have,
= (1 + cos α)(1 + cos β)(1 + cos γ)
= 2 cos2 (α/2).2 cos2 (β/2).2 cos2 (γ/2)
= 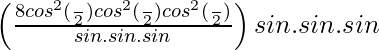
= 
= 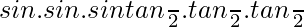
Therefore, sin α sin β sin γ is the member of equality.
Hence proved.
Question 82. If sin θ + cos θ = x, prove that sin6 θ + cos6 θ = 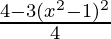 .
.
Solution:
We are given,
=> sin θ + cos θ = x
On squaring both sides, we get,
=> (sin θ + cos θ)2 = x2
=> sin2 θ + cos2 θ + 2 sin θ cos θ = x2
=> 2 sin θ cos θ = x2 − 1
=> sin θ cos θ = (x2 − 1)/2 . . . . (1)
We know,
=> sin2 θ + cos2 θ = 1
Cubing on both sides, we get
=> (sin2 θ + cos2 θ)3 = 13
=> sin6 θ + cos6 θ + 3 sin2 θ cos2 θ (sin2 θ + cos2 θ) = 1
=> sin6 θ + cos6 θ = 1 – 3 sin2 θ cos2θ
From (1), we get,
=> sin6 θ + cos6 θ = 1 – 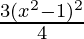
=> sin6 θ + cos6 θ = 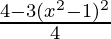
Hence proved.
Question 83. If x = a sec θ cos ϕ, y = b sec θ sin ϕ and z = c tan ϕ, show that, x2/a2 + y2/b2 − z2/c2 = 1.
Solution:
We are given, x = a sec θ cos ϕ, y = b sec θ sin ϕ, z = c tan ϕ
On squaring x, y, z, we get,
x2 = a2 sec2 θ cos2 ϕ or x2/a2 = sec2 θ cos2 ϕ . . . . (1)
y2 = b2 sec2 θ sin2 ϕ or y2/b2 = sec2 θ sin2 ϕ . . . . (2)
z2 = c2 tan2 ϕ or z2/c2 = tan2 ϕ . . . . (3)
Now L.H.S. = x2/a2 + y2/b2 − z2/c2
Using (1), (2) and (3), we get,
= sec2 θ cos2 ϕ + sec2 θ sin2 ϕ − tan2 ϕ
= sec2θ (cos2 ϕ + sin2 ϕ) − tan2 ϕ
= sec2θ (1) − tan2 ϕ
= sec2 θ − tan2 θ
= 1
= R.H.S.
Hence proved.
Question 84. If sin θ + 2 cos θ. Prove that 2 sin θ – cos θ = 2.
Solution:
We are given, sin θ + 2 cos θ = 1
On squaring both sides, we get,
=> (sin θ + 2 cos θ)2 = 12
=> sin2 θ + 4 cos2 θ + 4 sin θ cos θ = 1
=> 4 cos2 θ + 4 sin θ cos θ = 1 – sin2 θ
=> 4 cos2 θ + 4 sin θ cos θ – cos2 θ = 0
=> 3 cos2 θ + 4 sin θ cos θ = 0 . . . . (1)
We have, L.H.S. = 2 sin θ – cos θ
On squaring L.H.S., we get,
= (2 sin θ – cos θ)2
= 4 sin2 θ + cos2 θ – 4 sin θ cos θ
From (1), we get,
= 4 sin2 θ + cos2 θ + 3 cos2θ
= 4 sin2 θ + 4 cos2 θ
= 4(sin2 θ + cos2 θ)
= 4
So, we have,
=> (2 sin θ – cos θ)2 = 4
=> 2 sin θ – cos θ = 2
Hence proved.
Share your thoughts in the comments
Please Login to comment...