Class 10 RD Sharma Solutions – Chapter 11 Constructions – Exercise 11.1
Last Updated :
16 May, 2021
Question 1. Determine a point that divides a line segment of length 12 cm internally in the ratio 2 : 3. Also, justify your construction.
Solution:
Steps of construction:
Step 1. Draw a line segment AB =12cm.
Step 2. Through the A and B draw two parallel line on each sides of AB.
Step 3. Cut 2 equal parts on AX and 3 equal parts on BY such that AX1=X1X2 and BX1=Y1Y2=Y2Y3
Step 4. Join X2Y3 which intersects AB at P 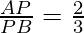
Justification:
In ∆AX2P and ∆BY3P, we have
∠APX2=∠BPY3 {Because they are vertically opposite angle}
∠X2AP=∠Y3BP
∆AX2P and ∆BY3P {Because AA similarity}
Therefore, 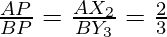 {Because of C.P.CT}
{Because of C.P.CT}

Question 2. Divide a line segment of length 9 cm internally in the ratio 4 : 3. Also, give justification of the construction.
Solution:
Steps of construction:
Step 1. Draw a line segment AB = 9 cm.
Step 2. Through the points, A and B, draw two parallel lines AX and BY on the opposite side of AB
Step 3. Cut 4 equal parts on AX and 3 equal parts on BY such AX1=X1X2=X2X3=X3X4 and BY1=Y1Y2=Y2Y3
Step 4. Join x4y3 which intersects AB at P.
Therefore, 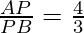
Justification:
In ∆PX4 and ∆BPY3, we have
∠APX4=∠BPY3 {Because they are vertically opposite angles}
∠PAX4=∠PBY3 {Because they are alternate interior angle}
∆APX4 ∆BPY3 {Because AA similarity}
Therefore, 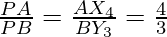 {Because of C.P.C.T}
{Because of C.P.C.T}

Question 3. Divide a line segment of length 14 cm internally in the ratio 2 : 5. Also, justify your construction.
Solution:
Steps of construction:
Step 1. Draw a line segment AB = 14 cm.
Step 2. Draw a ray AX making an acute angle with AB.
Step 3. From B, draw another ray BY parallel to AX.
Step 4. From AX, cut off 2 equal parts and from B, cut off 5 equal parts.
Step 5. Join 2 and 5 which intersects AB at P.
P is the required point which divides AB in the ratio of 2 : 5 internally.
Justification:
In ∆PX2 and ∆BPY5, we have
∠APX2=∠BPY5 (vertically opposite angles)
∠PAX2=∠PBY5 (Because they are alternate interior angle)
∆APX2 ∆BPY5 (Because AA similarity)
Therefore,
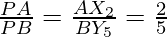
(Because of C.P.C.T)

Question 4. Draw a line segment of length 8 cm and divide it internally in the ratio 4 : 5.
Solution:
Steps of construction:
Step 1. Draw a line of 8cm.
Step 2. Through the points, A and B, draw two parallel lines AX and BY on the opposite side of AB
Step 3. Cut 4 equal parts AX and 3 equal parts on BY.
Step 4. Join x4y5 which intersects AB at P.
Justification:
In ∆PX4 and ∆BPY5, we have
∠APX4=∠BPY5 (vertically opposite angles)
∠PAX4=∠PBY5 (alternate interior angle)
∆APX4 ∆BPY5 (AA similarity)
Therefore,
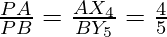
(Because of C.P.C.T)

Share your thoughts in the comments
Please Login to comment...