Class 10 RD Sharma Solution – Chapter 7 Statistics – Exercise 7.4 | Set 2
Last Updated :
03 Mar, 2021
Question 11. An incomplete distribution is given below :
| Variable | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 |
| Frequency | 12 | 30 | – | 65 | – | 25 | 18 |
You are given that the median value is 46 and the total number of items is 230.
(i) Using the median formula fill up missing frequencies.
(ii) Calculate the AM of the completed distribution.
Solution:
Let us assume p1, and p2 to be the missing frequencies
Median = 46 and N = 230
| Variable | Frequency (f) | cf |
| 10-20 | 12 | 12 |
| 20-30 | 30 | 42 |
| 30-40 | p1 | 42+p1 |
| 40-50 | 65 | 107+p1 |
| 50-60 | p2 | 107+p1+p2 |
| 60-70 | 25 | 132+p1+p2 |
| 70-80 | 18 | 150+p1+p2 |
| Total | 230 | |
∴ 150 + p1 + p2 = 230
⇒ p1+p2 = 230 – 150 = 80
∴ p2 = 80-p1 …..(i)
Since, median = 46 which lies in the class interval belonging to 40-50
∴ I = 40, f= 65, F = 42 +p1, h = 10
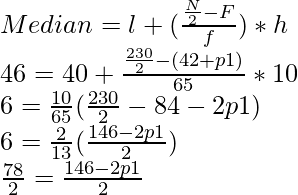
⇒ 39 = 73 – p1
⇒ p1 = 73 -39 = 34
∴ p2 – 80 – p1 = 80 – 34 = 46
Therefore, the missing frequencies are 34, and 46.
Let the assumed mean (A) be 45.
| Variable | Class Marks (x) | Frequency (f) |
d = x -A
A = 45
| fi * di |
| 10-20 | 15 | 12 | -30 | -360 |
| 20-30 | 25 | 30 | -20 | -600 |
| 30-40 | 35 | 34 | -10 | -340 |
| 40-50 | 45 – A | 65 | 0 | 0 |
| 50-60 | 55 | 46 | 10 | 460 |
| 60-70 | 65 | 25 | 20 | 500 |
| 70-80 | 75 | 18 | 30 | 540 |
| Total | | 230 | | 200 |
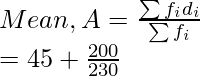
= 45 + 0.8695
= 45 + 0.87
= 45.87
Question 12. If the median of the following frequency distribution is 28.5 find the missing frequencies:
| Class interval | 0-10 | 20-30 | 30-40 | 40-50 | 50-60 | Total |
| Frequency | 5 | f1 | 15 | f2 | 5 | 60 |
Solution:
Mean = 28.5, N = 60
| Class interval | Frequency | c.f |
| 0-10 | 5 | 5 |
| 10-20 | f1 | 5 +f1 |
| 20-30 | 20 | 25 + f1 |
| 30-40 | 15 | 40 + f1 |
| 40-50 | f2 | 40 + f1 + f2 |
| 50-60 | 5 | 45 + f1 + f2 |
| Total | 60 | |
Therefore,
45 + f1 + f2 = 60
=> f1 + f2 = 60 – 45 = 15
=> f2 = 15 – f1
17 = 25 – f1
N/2 = 30
Now, Median = 28.5 and it lies in the class interval of 20-30
Therefore,
l = 20, F = 5 + f1, f= 20 and h = 10
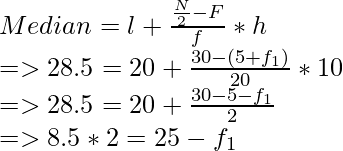
⇒ f1= 25 -17 = 8
and f2 = 15-f1 = 15-8 = 7
Therefore, the missing frequencies are 8 and 7 respectively.
Question 13. The median of the following data is 525. Find the missing frequency, if it is given that there are 100 observations in the data:
| Class Interval | Frequency | Class Interval | Frequency |
| 0-100 | 2 | 500-600 | 20 |
| 100-200 | 5 | 600-700 | f2 |
| 200-300 | f1 | 700-800 | 9 |
| 300-400 | 12 | 800-900 | 7 |
| 400-500 | 17 | 900-1000 | 4 |
Solution:
Median = 525, N = 100
| Class Interval | Frequency | c.f. |
| 0-100 | 2 | 2 |
| 100-200 | 5 | 7 |
| 200-300 | f1 | 7 + f1 |
| 300-400 | 12 | 19 + f1 |
| 400-500 | 17 | 36 + f1 |
| 500-600 | 20 | 56 + f1 |
| 600-700 | f2 | 56 + f1 + f2 |
| 700-800 | 9 | 65 + f1 + f2 |
| 800-900 | 7 | 72 + f1 + f2 |
| 900-1000 | 4 | 76 + f1 + f2 |
| Total | 100 | |
Therefore,
76 + f1 + f2 = 100 => f1 + f2 = 100 – 76 = 26
f2 = 24 – f1
Because,
Median = 525 which belongs to the interval 500-600
Now, l =500, F = 36 + f1, f =20, h = 100
Therefore,
M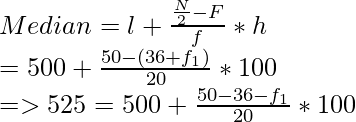
⇒ 525 – 500 = (14 -f1) x 5
⇒ 25 = 70- 5f1
⇒ 5f1 = 70 – 25 = 45
⇒ f1 = 455 = 9
and f2 = 24 – f1 = 24 – 9 = 15
Hence, we obtain the values for f1 = 9, f2 = 15.
Question 14. If the median of the following data is 32.5, find the missing frequencies.
| Class interval | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | Total |
| Frequency | f1 | 5 | 9 | 12 | f2 | 3 | 2 | 40 |
Solution:
Mean = 32.5 and N= 40
| Class interval | Frequency (f) | c.f. |
| 0-10 | f1 | f1 |
| 10-20 | 5 | 5 + f1 |
| 20-30 | 9 | 14 + f1 |
| 30-40 | 12 | 26 + f1 |
| 40-50 | f2 | 26 + f1 + f2 |
| 50-60 | 3 | 29 + f1 + f2 |
| 60-70 | 2 | 31 + f1 + f2 |
| | 40 | |
Now, we know,
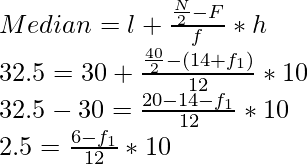
Solving, we get,
⇒ 2.5 x 12 = 60 – 10f1
⇒ 30 = 60 – 10f1
⇒ 10f1 = 60-30 = 30
⇒ f1 = 30/10 =3
∴ f2 = 9 – f1 = 9-3 = 6
Hence, f1 = 3, f2= 6
Question 15. Compute the median for each of the following data:
(i)
| Marks | No. of students | (ii) Marks | No. of students |
| Less than 10 | 0 | More than 150 | 0 |
| Less than 30 | 10 | More than 140 | 12 |
| Less than 50 | 25 | More than 130 | 27 |
| Less than 70 | 43 | More than 120 | 60 |
| Less than 90 | 65 | More than 110 | 105 |
| Less than 110 | 87 | More than 100 | 124 |
| Less than 130 | 96 | More than 90 | 141 |
| Less than 150 | 100 | More than 80 | 150 |
Solution:
(i) Less than
| Marks | c.f | f |
| 0-10 | 0 | 0 |
| 10-30 | 10 | 10 |
| 30-50 | 25 | 15 |
| 50-70 | 43 | 18 |
| 70-90 | 65 | 22 |
| 90-110 | 87 | 22 |
| 110-130 | 96 | 9 |
| 130-150 | 100 | 4 |
We have, N= 100
∴N/2 = 100/2 = 50 which lies in the class interval belonging to 70-90 (∵ 50 < 65 and > 43)
∴ l = 70, F =43 , f = 22 ,h = 20
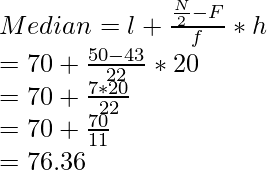
(ii) Greater than
| Marks | c.f | f |
| More than 150 (150-160) | 0 | 0 |
| 140-150 | 12 | 12 |
| 130-140 | 27 | 15 |
| 120-130 | 60 | 35 |
| 110-120 | 105 | 45 |
| 100-110 | 124 | 19 |
| 90-100 | 141 | 17 |
| 80-90 | 150 | 9 |
We have,
N = 150, N/2 = 150/2 = 75 which lies in the class interval belonging to 110-120 (∵ 75 > 105 and 75 > 60)
∴ l = 110, F = 60 , f=45, h= 10
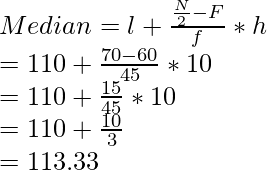
Question 16. A survey regarding the height (in cm) of 51 girls of class X of a school was conducted and the following data was obtained.
| Height in cm | Number of girls |
| Less than 140 | 4 |
| Less than 145 | 11 |
| Less than 150 | 29 |
| Less than 155 | 40 |
| Less than 160 | 46 |
| Less than 165 | 51 |
Find the median height.
Solution:
| Height (in cm) | No of girls (c.f) | F |
| 135 – 140 | 4 | 4 |
| 140 – 145 | 11 | 7 |
| 145 – 150 | 29 | 18 |
| 150 – 155 | 40 | 11 |
| 155 – 160 | 46 | 6 |
| 160 – 165 | 51 | 5 |
| | | 51 |
Here, ∑F/2 = 51/2 = 25.5 or 26 which lies in the class interval belonging to 145-150
Therefore,
l= 145, F= 11, f= 18, h= 5
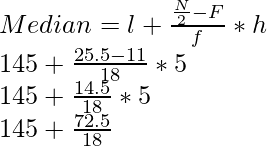
= 145 + 4.03 = 149.03
Question 17. A life insurance agent found the following data for distribution of ages of 100 policy holders. Calculate the median age, if policies are only given to persons having age 18 years onward but less than 60 years.
| Age in years | Number of policy holders |
| Below 20 | 2 |
| Below 25 | 6 |
| Below 30 | 24 |
| Below 35 | 45 |
| Below 40 | 78 |
| Below 45 | 89 |
| Below 50 | 92 |
| Below 55 | 98 |
| Below 60 | 100 |
Solution:
| Age in years |
No of policy holders
(c.f)
| f |
| 15-20 | 2 | 2 |
| 20-25 | 6 | 4 |
| 25-30 | 24 | 18 |
| 30-35 | 45 | 21 |
| 35-40 | 78 | 33 |
| 40-45 | 89 | 11 |
| 45-50 | 92 | 3 |
| 50-55 | 98 | 6 |
| 55-60 | 100 | 2 |
| Total | | 100 |
Here N = 100, N/2 = 100/2 = 50 which lies in the class interval of 35-40 ( ∵ 45 > 50> 78)
Therefore,
l = 35, F = 45, f= 33, h = 5
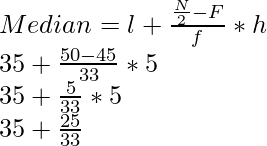
= 35 + 0.76 = 35.76
Question 18. The lengths of 40 leaves of a plant are measured correct to the nearest millimetre, and the data obtained is represented in the following table:
| Length (in mm) | 118-126 | 127-135 | 136-144 | 145-153 | 154-162 | 163-171 | 172-180 |
| No of leaves | 3 | 5 | 9 | 12 | 5 | 4 | 2 |
Find the mean length of leaf.
Solution:
|
Length (in mm)
(in exclusive form)
| No. of leaves (f) | c.f. |
| 117.5 – 126.5 | 3 | 3 |
| 126.5 – 135.5 | 5 | 8 |
| 135.5 – 144.5 | 9 | 17 |
| 144.5 – 153.5 | 12 | 29 |
| 153.5 – 162.5 | 5 | 34 |
| 162.5 – 171.5 | 4 | 38 |
| 171.5 – 180.5 | 2 | 40 |
N = 40, N/2 = 40/2 = 20 which lies in the class interval of 144.5-153.5 as 17 < 20 < 29
Therefore,
l= 144.5, F= 17, f= 12, h = 9
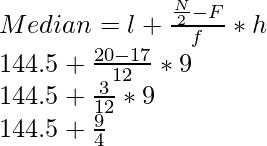
= 144.5 + 2.25 = 146.75
Question 19. An incomplete distribution is given as follows :
| Variable | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 |
| Frequency | 10 | 20 | ? | 40 | ? | 25 | 15 |
You are given that the median value is 35 and the sum of all the frequencies is 170. Using the median formula, fill up the missing frequencies.
Solution:
Median = 25 and ∑f= N = 170
Let us assume x and y to be the two missing frequencies
| Variable | Frequency | c.f |
| 0-10 | 10 | 10 |
| 10-20 | 20 | 30 |
| 20-30 | x | 30+x |
| 30-40 | 40 | 70+x |
| 40-50 | y | 70+x+y |
| 50-60 | 25 | 95+x+y |
| 60-70 | 15 | 110+x+y |
∴ 110 + x +y = 170
⇒ x + y = 170 – 110 = 60
Here, we have,
N = 170, N/2 = 170/2 = 85
Therefore, Median = 35 which lies in the class interval belonging to 30-40
Here l = 30, f= 40, F = 30 + x and h = 10
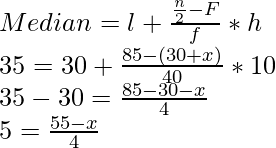
20 = 55 – x
⇒ x = 55 – 20 = 35
But,
x + y = 60
Solving for y, we get,
∴ y = 60 – x = 60 – 35 = 25
Hence missing frequencies x and y are 35 and 25.
Question 20. The median of the distribution given below is 14.4. Find the values of x and y, if the total frequency is 20.
| Class interval | 0-6 | 6-12 | 12-18 | 18-24 | 24-30 |
| Frequency | 4 | x | 5 | y | 1 |
Solution:
| Class interval | Frequency | Cumulative Frequency |
| 0-6 | 4 | 4 |
| 6-12 | x | 4+x |
| 12-18 | 5 | 9+x |
| 18-24 | y | 9+x+y |
| 24-30 | 1 | 10+x+y |
We know, n = 20
Therefore,
10 + x + y – 20,
=> x+y= 10 …(i)
Also,
Median = 14.4 which lies in the class interval belonging to 12-18
So, l = 12, f= 5, cf = 4 + x, h = 6
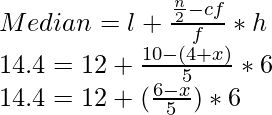
Solving for x, we get,
x = 6 ….(ii)
Also,
y = 6
Question 21. The median of the following data is SO. Find the values of p and q, if the sum of all the frequencies is 90.
| Marks: | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 |
| Frequency: | p | 15 | 25 | 20 | q | 8 | 10 |
Solution:
| Marks | Frequency | Cumulative Frequency |
| 20-30 | p | p |
| 30-40 | 15 | 15 + p |
| 40-50 | 25 | 40 + p = cf |
| 50-60 | 20 = f | 60 + p |
| 60-70 | q | 60 + p + q |
| 70-80 | 8 | 68 + p + q |
| 80-90 | 10 | 78 + p + q |
Given, N = 90
And, N/2 = 90/2 = 45 which lies in the class interval 50-60
Now,
Lower limit, l = 50, f= 20, cf= 40 + p, h = 10
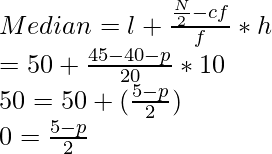
Obtaining values, we get,
∴ P = 5
Also, 78 +p + q = 90
⇒ 78 + 5 + q = 90
⇒ q = 90-83
∴ q = 7
Share your thoughts in the comments
Please Login to comment...