Class 10 RD Sharma Solution – Chapter 7 Statistics – Exercise 7.4 | Set 1
Last Updated :
03 Mar, 2021
Question 1. Following are the lives in hours of 15 pieces of the components of aircraft engine. Find the median:
715, 724, 725, 710, 729, 745, 694, 699, 696, 712, 734, 728, 716, 705, 719.
Solution:
On arranging the observations in ascending order, we have
694, 696, 699, 705, 710, 712, 715, 716, 719, 721, 725, 728, 729, 734, 745
Number of terms in the observation sequence is odd, i.e., N = 15
Now,
Median = (N + 1)/2th term
= (15 + 1)/2th term
= 8th term
Therefore, 716, which is the 8th term is the median of the data.
Question 2. The following is the distribution of height of students of a certain class in a certain city:
| Height (in cm): | 160 – 162 | 163 – 165 | 166 – 168 | 169 – 171 | 172 – 174 |
| No of students: | 15 | 118 | 142 | 127 | 18 |
Find the median height.
Solution:
| Class interval (exclusive) | Class interval (inclusive) | Class interval frequency | Cumulative frequency |
| 160 – 162 | 159.5 – 162.5 | 15 | 15 |
| 163 – 165 | 162.5 – 165.5 | 118 | 133(F) |
| 166 – 168 | 165.5 – 168.5 | 142(f) | 275 |
| 169 – 171 | 168.5 – 171.5 | 127 | 402 |
| 172 – 174 | 171.5 – 174.5 | 18 | 420 |
| | | N =420 | |
We have N = 420,
So, N/2 = 420/ 2 = 210
Now, The cumulative frequency just greater than N/2 is 275
Therefore, 165.5 – 168.5 is the median class s.t
L = 165.5, f = 142, F = 133 and h = (168.5 – 165.5) = 3
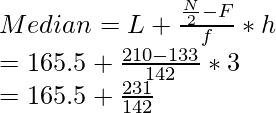
= 165.5 + 1.63
= 167.13
Question 3. Following is the distribution of I.Q of 100 students. Find the median I.Q.
| I.Q: | 55 – 64 | 65 – 74 | 75 – 84 | 85 – 94 | 95 – 104 | 105 – 114 | 115 – 124 | 125 – 134 | 135 – 144 |
| No of students: | 1 | 2 | 9 | 22 | 33 | 22 | 8 | 2 | 1 |
Solution:
| Class interval (exclusive) | Class interval (inclusive) | Class interval frequency | Cumulative frequency |
| 55 – 64 | 54.5 – 64.5 | 1 | 1 |
| 65 – 74 | 64.5 – 74.5 | 2 | 3 |
| 75 – 84 | 74.5 – 84.5 | 9 | 12 |
| 85 – 94 | 84.5 – 94.5 | 22 | 34(F) |
| 95 – 104 | 94.5 – 104.5 | 33(f) | 67 |
| 105 – 114 | 104.5 – 114.5 | 22 | 89 |
| 115 – 124 | 114.5 – 124.5 | 8 | 97 |
| 125 – 134 | 124.5 – 134.5 | 2 | 98 |
| 135 – 144 | 134.5 – 144.5 | 1 | 100 |
| | | N = 100 | |
N = 100,
Therefore, N/2 = 100/ 2 = 50
The cumulative frequency just greater than N/ 2 is 67 then the median class is (94.5 – 104.5) s.t,
L = 94.5, F = 33, h = (104.5 – 94.5) = 10
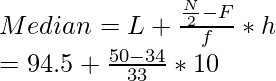
= 94.5 + 4.85
= 99.35
Question 4. Calculate the median from the following data:
| Rent (in Rs): | 15 – 25 | 25-35 | 35-45 | 45-55 | 55-65 | 65-75 | 75-85 | 85-95 |
| No of houses: | 8 | 10 | 15 | 25 | 40 | 20 | 15 | 7 |
Solution:
| Class interval | Frequency | Cumulative frequency |
| 15 – 25 | 8 | 8 |
| 25 – 35 | 10 | 18 |
| 35 – 45 | 15 | 33 |
| 45 – 55 | 25 | 58 (F) |
| 55 – 65 | 40(f) | 98 |
| 65 – 75 | 20 | 118 |
| 75 – 85 | 15 | 133 |
| 85 – 95 | 7 | 140 |
| | N = 140 | |
N = 140,
And, N/2 = 140/ 2 = 70
The cumulative frequency just greater than N/ 2 is 98 then median class is 55 – 65 s.t,
L = 55, f = 40, F = 58, h = 65 – 55 = 10
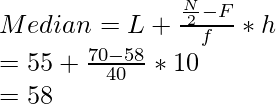
Question 5. Calculate the median from the following data:
| Marks below: | 0-10 | 10 – 20 | 20 – 30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 |
| No of students: | 15 | 35 | 60 | 84 | 96 | 127 | 198 | 250 |
Solution:
| Marks below | No. of students | Class interval | Frequency | Cumulative frequency |
| 10 | 15 | 0-10 | 15 | 15 |
| 20 | 35 | 10-20 | 20 | 35 |
| 30 | 60 | 20-30 | 25 | 60 |
| 40 | 84 | 30-40 | 24 | 84 |
| 50 | 96 | 40-50 | 12 | 96(F) |
| 60 | 127 | 50-60 | 31(f) | 127 |
| 70 | 198 | 60-70 | 71 | 198 |
| 80 | 250 | 70-80 | 52 | 250 |
| | | | N = 250 | |
N = 250,
And, N/2 = 250/ 2 = 125
The cumulative frequency just greater than N/ 2 is 127 then median class is 50 – 60 s.t,
L = 50, f = 31, F = 96, h = 60 -50 = 10
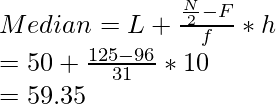
Question 6. Calculate the missing frequency from the following distribution, it being given that the median of the distribution is 24.
| Age in years: | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 |
| No of persons: | 5 | 25 | ? | 18 | 7 |
Solution:
Let us assume the unknown frequency to be x.
| Class interval | Frequency | Cumulative frequency |
| 0 – 10 | 5 | 5 |
| 10-20 | 25 | 30 (F) |
| 20-30 | x(f) | 30 + x |
| 30-40 | 18 | 48 + x |
| 40-50 | 7 | 55 + x |
| | N=170 | |
Given: Median = 24
Therefore,
Median class = 20 – 30; L = 20, h = 30 -20 = 10, f = x, F = 30
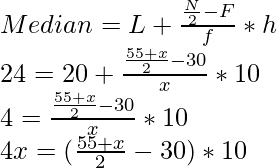
4x = 275 + 5x – 300
4x – 5x = – 25
– x = – 25
x = 25
Therefore, x = 25
Question 7. The following table gives the frequency distribution of married women by age at marriage.
| Age (in years) | Frequency | Age (in years) | Frequency |
| 15 – 19 | 53 | 40 – 44 | 9 |
| 20 – 24 | 140 | 45 – 49 | 5 |
| 25 – 29 | 98 | 45 – 49 | 3 |
| 30 – 34 | 32 | 55 – 59 | 3 |
| 35 – 39 | 12 | 60 and above | 2 |
Calculate the median and interpret the results.
Solution:
| Class interval (exclusive) | Class interval (inclusive) | Frequency | Cumulative frequency |
| 15 – 19 | 14.5 – 19.5 | 53 | 53(F) |
| 20 – 24 | 19.5 – 24.5 | 140(f) | 193 |
| 25 – 29 | 24.5 – 29.5 | 98 | 291 |
| 30 – 34 | 29.5 – 34.5 | 32 | 323 |
| 35 – 39 | 34.5 – 39.5 | 12 | 335 |
| 40 – 44 | 39.5 – 44.5 | 9 | 344 |
| 45 – 49 | 44.5 – 49.5 | 5 | 349 |
| 50 – 54 | 49.5 – 54.5 | 3 | 352 |
| 55 – 54 | 54.5 – 59.5 | 3 | 355 |
| 60 and above | 59.5 and above | 2 | 357 |
| | | N =357 | |
N = 357,
And, N/2 = 357/ 2 = 178.5
The cumulative frequency just greater than N/2 is 193,
Therefore, median class is 19.5 – 24.5 s.t
l = 19.5, f = 140, F = 53, h = 25.5 – 19.5 = 5
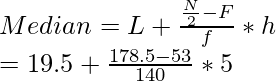
Median = 23.98, that implies that nearly half of the women are married between the ages of 15 and 25.
Question 8. The following table gives the distribution of the life time of 400 neon lamps:
| Life time: (in hours) | Number of lamps |
| 1500 – 2000 | 14 |
| 2000 – 2500 | 56 |
| 2500 – 3000 | 60 |
| 3000 – 3500 | 86 |
| 3500 – 4000 | 74 |
| 4000 – 4500 | 62 |
| 4500 – 5000 | 48 |
Find the median life.
Solution:
| Life time | Number of lamps fi | Cumulative frequency (cf) |
| 1500 – 2000 | 14 | 14 |
| 2000 – 2500 | 56 | 70 |
| 2500 – 3000 | 60 | 130(F) |
| 3000 – 3500 | 86 | 216 |
| 3500 – 4000 | 74 | 290 |
| 4000 – 4500 | 62 | 352 |
| 4500 – 5000 | 48 | 400 |
| | N = 400 | |
Now
N = 400
And the cumulative frequency just greater than n/2 (= 200) is 216, which belongs to the class interval 3000 – 3500
Median class = 3000 – 3500. Therefore,
(l) = 3000 and,(f) of median class = 86, (cf) of class preceding median class = 130 and (h) = 500
We have,
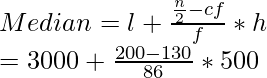
= 3000 + (35000/86)
= 3406.98 hrs, which is the median time of lamps.
Question 9. The distribution below gives the weight of 30 students in a class. Find the median weight of students:
| Weight (in kg): | 40 – 45 | 45 – 50 | 50 – 55 | 55 – 60 | 60 – 65 | 65 – 70 | 70 – 75 |
| No of students: | 2 | 3 | 8 | 6 | 6 | 3 | 2 |
Solution:
| Weight (in kg) | Number of students fi | Cumulative frequency (cf) |
| 40 – 45 | 2 | 2 |
| 45-50 | 3 | 5 |
| 50-55 | 8 | 13 |
| 55-60 | 6 | 19 |
| 60-65 | 6 | 25 |
| 65-70 | 3 | 28 |
| 70-75 | 2 | 30 |
The cf value just greater than n/ 2 (i.e. 30/ 2 = 15) is 19, belongs to class interval 55 – 60.
Therefore,
Median class = 55 – 60
where,
(l) of median class = 55, (f) of median class = 6, (cf) = 13 and (h) = 5
We have,
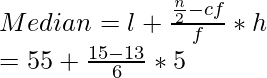
= 55 + 10/6 = 56.666 which is approximately 56.67 kg.
Question 10. Find the missing frequencies and the median for the following distribution if the mean is 1.46
| No. of accidents: | 0 | 1 | 2 | 3 | 4 | 5 | Total |
| Frequencies (no. of days): | 46 | ? | ? | 25 | 10 | 5 | 200 |
Solution:
| No. of accidents (x) | No. of days (f) | fx |
| 0 | 46 | 0 |
| 1 | x | x |
| 2 | y | 2y |
| 3 | 25 | 75 |
| 4 | 10 | 40 |
| 5 | 5 | 25 |
| | N = 200 | Sum = x + 2y + 140 |
Since, we know,
N = 200
Substituting values, we get,
⇒ 46 + x + y + 25 + 10 + 5 = 200
⇒ x + y = 200 – 46 – 25 – 10 – 5
⇒ x + y = 114…… (i)
Also, Mean = 1.46
⇒ Sum/ N = 1.46
Substituting values,
⇒ (x + 2y + 140)/ 200 = 1.46
⇒ x + 2y = 292 – 140
⇒ x + 2y = 152 …….(ii)
Solving from (i) and (ii), we get
x + 2y – x – y = 152 – 114
⇒ y = 38
And, x = 114 – 38 = 76 (from equation (i))
Now, putting the values, we get,
N = 200 N/2 = 200/2 = 100
So, the cumulative frequency just greater than N/2 is 122
And, therefore, the median is 1.
Share your thoughts in the comments
Please Login to comment...