Class 10 NCERT Solutions- Chapter 8 Introduction To Trigonometry – Exercise 8.1

Question 1. In ∆ ABC, right-angled at B, AB = 24 cm, BC = 7 cm. Determine :

(i) sin A, cos A (ii) sin C, cos C

Solution:

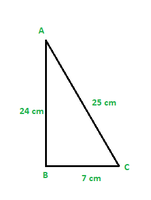
Using Pythagoras theorem for ΔABC

AC² = AB² + BC²

= (24 cm)² + (7 cm)²

= (576 + 49) cm²

= 625 cm²

∴AC = 25 cm       

(i) sin A = opp/hyp

    sin A = 7/25

    cos A = adj/hyp = 24/25

    cos A = 24/25

(ii) sin C = opp/hyp

     sin C = 24/25

     cos C = adj/hyp

     cos C = 7/25

Question 2. In Fig. 8.13, find tan P – cot R.

Solution:

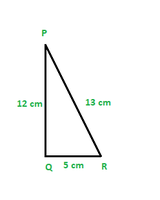
Applying Pythagoras theorem for ΔPQR, we obtain

PR² = PQ² + QR²

(13 cm)² = (12 cm)² + QR²

169 cm² = 144 cm² + QR²

25 cm² = QR²

QR = 5 cm

tan P = opp/adj

tan P = 5/12

cot R = adj/opp

cot R = 5/12

tan P – cot R = 5/12 – 5/12 = 0

Question 3. If sin A = 3/4, calculate cos A and tan A.

Solution:

Using sin²A + cos²A = 1

(3/4)² + cos²A = 1

cos²A = 1 – (3/4)² = 1 – 9/16

cos A = 7^1/2/4

tan A = sin A/cos A

tan A = (3/4)/(7^1/2/4)

tan A = 3/7^1/2

Question 4: Given 15 cot A = 8. Find sin A and sec A

Solution:

Given, 15 cot A = 8

               cot A = 8/15

tan A = 1/cot A

tan A = 15/8

Using, 1 + tan²A = sec²A

           1 + (15/8)² = sec²A

           289/64 = sec²A

           sec A = 17/8

We know, cos²A = 1/sec²A

                cos²A = 64/289

               sin²A = 1 – cos2A

               sin²A = 225/289

sin A = 15/17

Question 5: Given sec θ = 13/12, calculate all other trigonometric ratios.

Solution.

Using Pythagoras theorem,

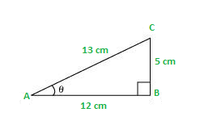
sin θ = 5/13

cos θ = 12/13

tan θ = 5/12

cosec θ = 13/5

cot θ = 12/5

Question 6: If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.

Solution:

Let us consider a ΔABC in which CD ⊥ AB.

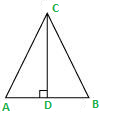
It is given that cos A = cos B

AD/AC = BD/BC     … (1)

We need to prove ∠A = ∠B. To prove this, we need to extend AC to P such that BC = CP.

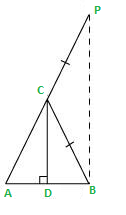
From equation (1), we obtain

AD/BD = AC/BC

AD/BD = AC/CP    (BC = CP by construction)

By using the converse of B.P.T (Basic Proportionality Theorem),

CD||BP

∠ACD = ∠CPB (Corresponding angles) … (3)

And, ∠BCD = ∠CBP (Alternate interior angles) … (4)

By construction, we have BC = CP.

∴ ∠CBP = ∠CPB (Angle opposite to equal sides of a triangle) … (5)

From equations (3), (4), and (5), we obtain

∠ACD = ∠BCD … (6)

In ΔCAD and ΔCBD,

∠ACD = ∠BCD (Using equation (6))

∠CDA = ∠CDB (Both 90°)

Therefore, the remaining angles should be equal.

∴∠CAD = ∠CBD

⇒ ∠A = ∠B

Question 7: If cot θ = 7/8, evaluate

(i) ((1 + sinθ) * (1 – sinθ))/(1 + cosθ) * (1 – cosθ)))

(ii) cot²θ

Solution:

(i) Using (a + b) * (a – b) = a² – b² in numerator and denominator

We get

(1 – sin²θ)/(1 – cos²θ)

Using sin²θ + cos²θ = 1

We get

cos²θ/sin²θ = cot²θ

Now

cot²θ = (7/8)2 = 49/64

(ii) cot²θ = (7/8)2 = 49/64

Question 8. If 3 cot A = 4, Check whether (1 – tan²A)/(1 + tan²A) = cos²A – sin²A

Solution.

We know that, tanA = sinA / cosA   ….(1)

Using (1) on L.H.S

= (1 – sin²A/cos²A)/(1 + sin²A/cos²A)

which on rearranging becomes

= (cos²A – sin²A)/(cos²A + sin²A)

Using the identity,

cos²A + sin²A = 1

LHS becomes

= (cos²A – sin²A)

This is equal to RHS.

LHS = RHS (for every value of cot A)

Hence, Proved.

Question 9: In ΔABC, right-angled at B. If tan A = 1/(3^1/2), find the value of

(i) sin A cos C + cos A sin C

(ii) cos A cos C − sin A sin C

Solution:

Using Pythagoras theorem

(AB)² + (BC)² = (AC)²

(31/2)² + (1)² = (AC)²

which gives

AC = 2 cm

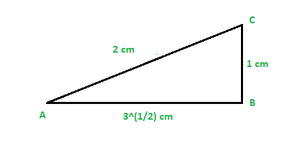
Using formulas

sin A = 1/2

sin C = 3^1/2/2

cos A = 3^1/2/2

cos C = 1/2

Now, (i) sin A cos C + cos A sin C

Substituting the values

= (1/2) * (1/2) + (3^1/2/2) * (3^1/2/2)

= 1/4 + 3/4

= 1

Now, (ii) cos A cos C − sin A sin C

Substituting the values

= (3^1/2/2) * (1/2) – (1/2) * (3^1/2/2)

= 3^1/2/4 – 3^1/2/4

= 0

Question 10: In ΔPQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.

Solution:

Given that, PR + QR = 25

PQ = 5

Let PR be x cm.

Therefore, QR = 25 − x cm

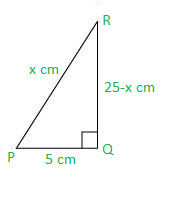
Applying Pythagoras theorem in ΔPQR, we obtain

PR² = PQ² + QR²

x² = (5)² + (25 − x)²

x² = 25 + 625 + x² − 50x

50x = 650

x = 13

Therefore, PR = 13 cm

QR = (25 − 13) cm = 12 cm

Now,

sin P = QR/PR = 12/13

cos P = PQ/PR = 5/13

tan P = QR/PQ = 12/5

Question 11. State whether the following are true or false. Justify your answer.

(i) The value of tan P is always less than 1.

(ii) sec A = 12/5 for some value of angle A.

(iii) cos A is the abbreviation used for the cosecant of angle A.

(iv) cot A is the product of cot and A

(v) sin θ = 4/3, for some angle θ

Solution:

(i) Consider a ΔPQR, right-angled at Q as shown below.

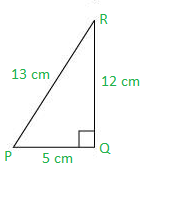
Here tan P = 12/5 which is surely greater than 1.

Therefore, the statement is false.

(ii) Consider ΔABC with AB = 5 cm, AC = 12 cm and BC = x cm

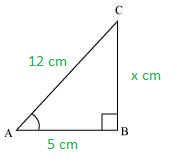
Using Pythagoras theorem in ΔABC

(AB)² + (BC)2 = (AC)2

52 + x2 = 122

x = (144 – 25)1/2

x = (119)1/2

x = 10.9 cm

AB < BC < AC

So this triangle is valid,

Therefore, given statement is true.

(iii) Abbreviation used for cosecant A is cosec A. And cos A is the abbreviation used for cosine A.

Hence, the given statement is false.

(iv) cot A is not the product of cot and A. It is the cotangent of ∠A.

Hence, the given statement is false.

(v) sin θ = 4/3 

In a right-angled triangle, hypotenuse is always greater than the remaining two sides. Therefore, such value of sin θ is not possible.

Hence, the given statement is false