Calculate the average, variance and standard deviation in Python using NumPy
Last Updated :
08 Oct, 2021
Numpy in Python is a general-purpose array-processing package. It provides a high-performance multidimensional array object and tools for working with these arrays. It is the fundamental package for scientific computing with Python. Numpy provides very easy methods to calculate the average, variance, and standard deviation.
Average
Average a number expressing the central or typical value in a set of data, in particular the mode, median, or (most commonly) the mean, which is calculated by dividing the sum of the values in the set by their number. The basic formula for the average of n numbers x1, x2, ……xn is
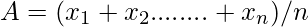
Example:
Suppose there are 8 data points,
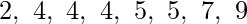
The average of these 8 data points is,
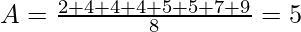
Average in Python Using Numpy:
One can calculate the average by using numpy.average() function in python.
Syntax:
numpy.average(a, axis=None, weights=None, returned=False)
Parameters:
a: Array containing data to be averaged
axis: Axis or axes along which to average a
weights: An array of weights associated with the values in a
returned: Default is False. If True, the tuple is returned, otherwise only the average is returned
Example 1:
Python
import numpy as np
list = [2, 4, 4, 4, 5, 5, 7, 9]
print(np.average(list))
|
Output:
5.0
Example 2:
Python
import numpy as np
list = [2, 40, 2, 502, 177, 7, 9]
print(np.average(list))
|
Output:
105.57142857142857
Variance
Variance is the sum of squares of differences between all numbers and means. The mathematical formula for variance is as follows,
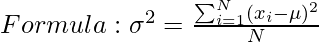
Where,
? is Mean,
N is the total number of elements or frequency of distribution.
Example:
Let’s consider the same dataset that we have taken in average. First, calculate the deviations of each data point from the mean, and square the result of each,
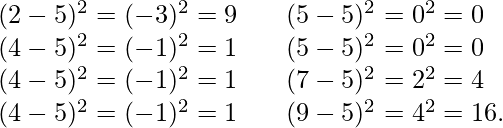
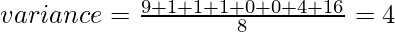
Variance in Python Using Numpy:
One can calculate the variance by using numpy.var() function in python.
Syntax:
numpy.var(a, axis=None, dtype=None, out=None, ddof=0, keepdims=<no value>)
Parameters:
a: Array containing data to be averaged
axis: Axis or axes along which to average a
dtype: Type to use in computing the variance.
out: Alternate output array in which to place the result.
ddof: Delta Degrees of Freedom
keepdims: If this is set to True, the axes which are reduced are left in the result as dimensions with size one
Example 1:
Python
import numpy as np
list = [2, 4, 4, 4, 5, 5, 7, 9]
print(np.var(list))
|
Output:
4.0
Example 2:
Python
import numpy as np
list = [212, 231, 234, 564, 235]
print(np.var(list))
|
Output:
18133.359999999997
Standard Deviation
Standard Deviation is the square root of variance. It is a measure of the extent to which data varies from the mean. The mathematical formula for calculating standard deviation is as follows,
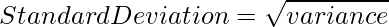
Example:
Standard Deviation for the above data,

Standard Deviation in Python Using Numpy:
One can calculate the standard deviation by using numpy.std() function in python.
Syntax:
numpy.std(a, axis=None, dtype=None, out=None, ddof=0, keepdims=<no value>)
Parameters:
a: Array containing data to be averaged
axis: Axis or axes along which to average a
dtype: Type to use in computing the variance.
out: Alternate output array in which to place the result.
ddof: Delta Degrees of Freedom
keepdims: If this is set to True, the axes which are reduced are left in the result as dimensions with size one
Example 1:
Python
import numpy as np
list = [2, 4, 4, 4, 5, 5, 7, 9]
print(np.std(list))
|
Output:
2.0
Example 2:
Python
import numpy as np
list = [290, 124, 127, 899]
print(np.std(list))
|
Output:
318.35750344541907
Share your thoughts in the comments
Please Login to comment...