Angle between Two Vectors Formula

Last Updated : 10 Apr, 2024

Angle between two vectors is the angle between their tails and this angle can be easily found using cross product and dot product of vector formulas. Angle between two vectors always lies between 0° and 180°.

In this article we will learn about, angle between two vectors, definition, formulas, and examples in detail.

What is Angle Between Two Vectors?

Angle between two vectors is the angle formed at the intersection of their tails. Angle between two vectors can be, acute, right, or obtuse, depending on the direction of the vectors.

Angle between two vectors is found using two formulas:

Using Dot Product of Vectors
Using Cross Product of Vectors

This is explained in the formula below.

Angle Between Two Vectors Formulas

Angle between two vectors is easily and most commonly found using scalar product of vectors.

Two vector A and B

Dot product of A and B is given by,

$\vec{A}.\vec{B}$ = |A| |B| cosθ.

Special Cases

When angle between vectors are 0 degree.

That is θ = 0°

⇒ |A| |B| cosθ

⇒ |A| |B| cos0°

⇒ |A| |B| [cos0° = 1]

When angle between vectors are 180 degree.

⇒ |A| |B| cosθ

⇒ |A| |B| cos180°

⇒ – |A| |B| [cos180° = -1]

When angle between vectors are 90 degree.

⇒ |A| |B| cosθ

⇒ |A| |B| cos90°

⇒ |A| |B| × 0 [cos90° = 0]

⇒ 0

Formula For Angle Between Two Vectors

Cosine of the angle between two vectors is equal to the sum of the product of the individual constituents of the two vectors, divided by the product of the magnitude of the two vectors.

Two Vectors A and B

$\vec{A}.\vec{B}$ =| A | | B | cosθ.

cosθ= $\frac{\vec{A}.\vec{B}}{|A|.|B|}$

θ= cos^-1 $\frac{\vec{A}.\vec{B}}{|A|.|B|}$

In cartesian Form,

A = A_xi + A_yj + A_zk

B= B_xi + B_yj + B_zk

cos θ = $\frac{(Ax.Bx+Ay.By+Az.Bz)}{(\sqrt{Ax^2+Ay^2+Az^2}×\sqrt{Bx^2+By^2+Bz^2})}$

Properties of Dot product

Dot product is commutative

$\vec{A}.\vec{B}=\vec{B}.\vec{A}$

Dot product is Distributive

$\vec{A}.(\vec{B}+\vec{C})=(\vec{A}.\vec{B}+\vec{A}.\vec{C})$

Angle between two vectors lies between 0 ≤ θ ≤ 180. When the tails or heads of both the vectors coincide, then the angle between vectors is calculated.

Tail Coincide

Head Coincide

Sample Problems Angle between Two Vectors Formula

Problem 1: Find the angle between vectors (If they form an equilateral triangle)

a and b vectors
b and c vectors
a and c vectors

Equilateral Triangle formed by a, b, c vector

Solution:

a and b vectors
For vector a and b, head of both the vectors coincide with each other, hence angle between a and b vector is same as the angle between two sides of equilateral triangle = 60°.

b and c vectors:
From the above figure, we see that head or tail of the b and c vector does not coincide with each other.

So, by using the property- A vector remains unchanged if it is transmitted parallel to itself.

Vector c is shifted parallel to itself
Now we see the tail of vectors b and c are coincide with each other, therefore is the same as the exterior angle make with an equilateral triangle = 120°.

a and c vectors
The tail of a and c coincide
For vectors a and c, the tail of both the vectors coincide with each other, hence the angle between the a and c vector is the same as the angle between two sides of the equilateral triangle = 60°.

Problem 2: Find angles between vectors if they form an isosceles right-angle triangle.

a and b vector
b and c vector
a and c vectors

Solution:

a and b vector
Right angle Isosceles Triangle
From the above figure, we see that head or tail of a and b vector does not coincide with each other. So, by using the property- A vector remains unchanged if it is transmitted parallel to itself.

a vector is shifted parallel to itself
Now, a and b vectors tails coincide with each other and make an angle the same as the exterior angle of a right angle isosceles triangle = 135°.

b and c vector
Right angle Isosceles Triangle
From the above figure, b and c vector head or tails does not coincide with each other. So, by using the property, a vector remains unchanged if it is transmitted parallel to itself.

b vector is shifted parallel to itself
Now, b and c vectors tails coincide with each other and make an angle the same as the exterior angle of a right angle isosceles triangle = 135°.

a and c vectors
Right angle Isosceles Triangle
From the above figure, a and c vector head or tails do not coincide with each other. So, by using the property- A vector remains unchanged if it is transmitted parallel to itself.

c vector is moved parallel to itself
Now, a and c vectors tails coincide with each other and make an angle the same as the right angle of isosceles triangle = 90°.

Problem 3: Find angle between the vectors A = i + j + k and vector B = -2i – 2j – 2k.

Solution:

From the formula,

A = A_xi + A_yj + A_zk

B= B_xi + B_yj + B_zk

cosθ= $\frac{(Ax.Bx+Ay.By+Az.Bz)}{(\sqrt{Ax^2+Ay^2+Az^2}×\sqrt{Bx^2+By^2+Bz^2})}$

Here in the Given question,

A= i + j + k

B= -2i -2j -2k

Substituting the values in the formula

⇒ cosθ = $\frac{(1.(-2)+1.(-2)+1.(-2))}{(\sqrt{1^2+1^2+1^2}×\sqrt{(-2)^2+(-2)^2+(-2)^2})}$

⇒ cosθ = $\frac{(-2-2-2)}{(\sqrt{1+1+1}×\sqrt{4+4+4})}$

⇒ cosθ = $\frac{-6}{(\sqrt{3}×\sqrt{12})}$

⇒ cosθ = $\frac{-6}{(\sqrt{36})}$

⇒ cosθ = -6/6

⇒ cosθ= -1

⇒ θ = 180°

Problem 4: Find angle between vector A = 3i + 4j and B = 2i + j

Solution:

A = A_xi + A_yj + A_zk

B = B_xi + B_yj + B_zk

cosθ = $\frac{(Ax.Bx+Ay.By+Az.Bz)}{(\sqrt{Ax^2+Ay^2+Az^2}×\sqrt{Bx^2+By^2+Bz^2})}$

Here Given,

A= 3i + 4j + 0k

B= 2i + j + 0k

Substituting the values in the formula,

⇒ cosθ = $\frac{(3.2+4.1+0.0)}{(\sqrt{3^2+4^2+0^2}×\sqrt{2^2+1^2+0^2})}$

⇒ cosθ = $\frac{(6+4+0)}{(\sqrt{9+16+0}×\sqrt{4+1+0})}$

⇒ cosθ = $\frac{(10)}{(\sqrt{25}×\sqrt{5})}$

⇒ cosθ = $\frac{(10)}{(\sqrt{125})}$

⇒ θ = cos^-1 ( $\frac{(10)}{5.(\sqrt{5})}$ )

⇒ θ = cos^-1 ( $\frac{2}{(\sqrt{5})}$ )

Problem 5: Find the angle between vector A = i + j and Vector B = j + k.

Solution:

From the formula,

A = A_xi + A_yj + A_zk

B = B_xi + B_yj + B_zk

cosθ = 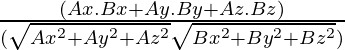$\frac{(Ax.Bx+Ay.By+Az.Bz)}{(\sqrt{Ax^2+Ay^2+Az^2}×\sqrt{Bx^2+By^2+Bz^2})}$

Here in the Given question,

⇒ A = i + j

⇒ B = j + k

⇒ cosθ = 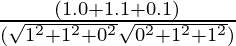$\frac{(1.0+1.1+0.1)}{(\sqrt{1^2+1^2+0^2}×\sqrt{0^2+1^2+1^2})}$

⇒ cosθ = $\frac{(1)}{(\sqrt{1+1+0}×\sqrt{0+1+1})}$

⇒ cosθ = $\frac{1}{(\sqrt{2}×\sqrt{2})}$

⇒ θ = cos^-1 (1/2)

⇒ θ = 60°