What is the Principle of Moments?
Last Updated :
29 Nov, 2022
A body is said to be in equilibrium if the forces and moments applied on the body cancel each other out and there is no net force and moment on the body. It is said to be rotational equilibrium if the net moments applied across it in the clockwise and anti-clockwise directions are zero. This analysis of moments and equilibrium is an integral part of the rotational mechanics. This analysis helps in determining the resulting motion of the rigid bodies. Let’s look at these concepts in detail.
Rigid Body in Equilibrium
A rigid body is said to be in equilibrium if both the linear momentum and angular momentum of the center of gravity are not changing with time. In other words, the net force and the torques on the body are zero. Such a body should not possess any linear or angular acceleration. Consider a body on which forces F1, F2, F3 … Fn and torques T1, T2, T3, T4, …Tn is applied. In this case,
- The Vector sum of all the forces being applied to the body is zero. F1 + F2 + F3 … + Fn = 0
- The vector sum of all the torques being applied to the body is zero. T1 + T2 + T3 … + Tn = 0
If the net forces and torque acting on the body do not change with time, the angular and linear momentum stays constant.
Principle of Moments
Consider an ideal lever, as given in the figure below. An ideal lever is nothing but a light rod (ideally negligible mass) that is pivoted at a point along its length. This point is called a fulcrum. A see-saw for children playing in the parks is an example of a lever system. The figure below shows two forces F1 and F2 acting on the lever. The pivot point of the lever is at a distance of d1 and d2 from the forces F1 and F2 respectively.

Assuming that the lever system is in equilibrium. Let R denote the reaction on body, the suppose at pivot point; R is directed opposite to the forces F1 and F2. Since the body is in both rotational and translation equilibrium,
R – F1 – F2 = 0 …. (1)
d1F1 – d2F2= 0 …. (2)
anti-clockwise moments are taken as negative.
Equation (2) can be re-written as,
d1F1 = d2F2
This equation is called the principle of moments equation for the above system. The ratio 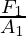 and
and 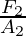 is called the mechanical advantage (M.A).
is called the mechanical advantage (M.A).
Formally, the principle of moments have defined as,
When a number of forces act on a rigid body and the body is in equilibrium, then the algebraic sum of moments in the clockwise direction is equal to the algebraic sum of moments in clockwise direction. In other words, the algebraic sum of moments due to all of the forces is zero.
Sample Problems
Question 1: In the figure given below, the distance and forces are given as d1 = 1m, d2 = 2m, F1 = 2N. Find the value of F2

Answer:
Since the body is in equilibrium, the algebraic sum of moments must be zero.
d1F1 – d1F2= 0
Given: d1 = 1m, d2 = 2m, F1 = 2N and F2 = ?
plugging these values in the equation,
d1F1 – d1F2= 0
⇒ (1)(2) – (2)(F2) = 0
⇒ F2 = 1N
Question 2: In the figure given below, the distance and forces are given as d1 = 1.5m, d2 = 5m, F1 = 10N. Find the value of F2

Answer:
Since the body is in equilibrium, the algebraic sum of moments must be zero.
d1F1 – d1F2= 0
Given: d1 = 1.5m, d2 = 5m, F1 = 10N and F2 = ?
plugging these values in the equation,
d1F1 – d1F2= 0
⇒ (1.5)(10) – (5)(F2) = 0
⇒ F2 = 3N
Question 3: In the figure given below, the distance and forces are given as d1 = 1.5m, d2 = 2m,d3 = 5m F1 = 10N F2 = 5N F3 = 4N. Find the whether the system will be in rotational equilibrium or not.

Answer:
To analyze the equilibrium, principle of moment is used.
Calculating the moments for the system
d1F1 + d2F2 – d3F3
⇒ (1.5)(10) + (2)(5) – (5)(4)
⇒ 15 + 10 -20
⇒ 5N
Since the total sum of moments is not zero. The system is not in rotational equilibrium.
Question 4: In the figure given below, the distance and forces are given as d1 = 5m, d2 = 4m,d3 = 10m F1 = 10N F2 = 5N F3 = 4N. Find the whether the system will be in rotational equilibrium or not.

Answer:
To analyze the equilibrium, principle of moment is used.
Calculating the moments for the system
d1F1 + d2F2 – d3F3
⇒ (5)(10) + (4)(5) – (10)(4)
⇒ 50 + 20 -40
⇒ 30
Since the total sum of moments is not zero. The system is not in rotational equilibrium.
Question 5: A 3m ladder of weight 20Kg is leaning on a frictionless wall. Its feet rest on the floor 1m from the wall. Find the reaction forces from the wall and the floor.

Answer:
Using Pythagoras theorem,
QR = 2√2m
Ladders weight acts from the center of the ladder, force from flow is F2 and from the wall is F1.
F2. is decomposed into normal force N and friction F.
Translational equilibrium,
In the horizontal direction, F- F1. = 0
In the vertical direction, N – W = 0
N = W
⇒ N = (20)(9.8)
⇒ N = 196 N
For rotational equilibrium around point A,
2√2F – (W/2) = 0
⇒ F = W/2√2
F = 34.6N = F1
F2 = 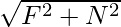
F2 = 199 N
Share your thoughts in the comments
Please Login to comment...