Angular Momentum in Case of Rotation About a Fixed Axis
Last Updated :
21 Jul, 2021
When a rigid body rotates around a fixed axis, it is called rotational motion. Rotational motion can be seen almost everywhere in daily lives. From the wheels of a car to the hands of the clock. All these objects are making rotational motion around a fixed axis. Similar to linear motion, rotation motion also involves velocity, acceleration, and momentum. These quantities are termed angular velocity, angular acceleration, and angular momentum in the case of rotational motion. Let’s look at the concept of angular momentum in detail.
Angular Velocity
Suppose a body is rotating around some fixed axis. Then the body changes its angle with time. Denoting the angle by θ, the angular velocity is defined as the rate of change of the angle of the body. Angular velocity is denoted by 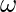 . If the body is rotating at a constant rate, the average angular velocity is used,
. If the body is rotating at a constant rate, the average angular velocity is used,
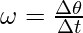
In the cases where the rotational motion is not constant, instantaneous angular velocity is calculated.


As shown in the figure, the angular velocity is directed towards the fixed axis. Linear velocity “v” of the particle can also be expressed in terms of the angular velocity.
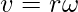
Angular Momentum
The motion of a rigid body is composed of translatory motion and rotational motion. It is known that force is needed to bring the body into translatory motion. Torque is analogous to force in rotational motion. Torque brings a change in the angular momentum of the system. Angular momentum is analogous to linear momentum in the case of translatory motion.
In the figure, a particle is given whose position vector with respect to the origin O is “r”. “p” denotes the linear momentum of the particle moving around that point. In that case, the angular momentum is given by,
l = r × p
This is the cross–product of the position vector and the linear momentum vector.
The magnitude of the vector is given by,
l = rpsin(θ)

The relation between the torque and force can also be derived from these equations. Differentiating the above equation,
l = r × p
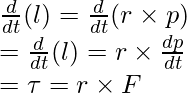
Angular Momentum of a System of Particles
Often, bodies are not point masses. They contain more than one particle. Let us assume that the body consists of n particles each of which has a position vector ri and momentum denoted by pi. In that case, the angular momentum of the system is given by the vector sum of the individual momentum of the particles.
L = l1 + l2 + l3 + .. ln
Each particle has an angular momentum which is given by,
li = ri x pi
L = r1 x p1 + r2 x p2 + r3 x p3 …. rn x pn
Sample Problems
Question 1: Find angular momentum of particle revolving around the origin at a distance of 5 m with linear momentum of 50Kg/s.
Answer:
Angular Momentum is given by,
l = rpsin(θ)
Given: r = 5 m, p = 50Kgm/s and θ = 90°.
l = rpsin(θ)
l = (5)(50)sin(90)
l = 250
Question 2: Find the angular momentum of a particle revolving around the origin at a distance of 10m with linear momentum of 10Kg/s. The angle between the position vector and momentum is 30°.
Answer:
Angular Momentum is given by,
l = rpsin(θ)
Given: r = 10m, p = 10Kgm/
l = rpsin(θ)
l = (10)(10)sin(30)
l = 50
Question 3: Find the angular momentum of a particle revolving around the origin at a distance of 1.5m with a linear momentum of 100Kgm/s. The angle between the position vector and momentum is 60°.
Answer:
Angular Momentum is given by,
l = rpsin(θ)
Given: r = 5 m, p = 50Kgm/s
l = rpsin(θ)
l = (1.5)(100)sin(60)
l = 75√3
Question 4: Position vector and linear momentum of a body is given by r = 3i + 4j + k m and p = 5j Kg/s. Find the angular momentum.
Answer:
Angular Momentum is given by,
l = r × p
Given: r = 3i + 4j + k, p = 5j.

Question 5: Position vector and linear momentum of a body is given by r = i + j + k m and p = i + j Kg/s. Find the angular momentum.
Answer:
Angular Momentum is given by,
l = r × p
Given: r = i + j + k, p = i + j
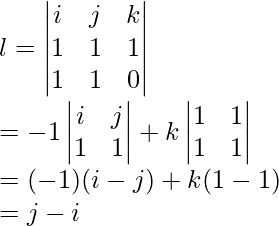
Question 6: Find the angular momentum of the system of two particles revolving around the origin at a distance of 5 m with a linear momentum of 50Kg/s and 10 Kg/s.
Answer:
Angular Momentum is given by,
l = rpsin(θ)
Given: r = 5 m, p1 = 50Kgm/s, p2 = 10Kgm/s and the angle is a right angle.
Since the system consists of two particles. The total angular momentum will be the sum of the angular momentum of these particles.
l = rp1 + rp2
l = (5)(50) + (5)(10)
l = 250 + 50
l = 300
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...