The relation between speed, distance, and time has been taught for a very long time and a very simple formula is known, S = D/T (speed=distance/time), this formula is the most basic formula to find out the speed, distance, or time of an object/body. However, this formula is only valid for the constant velocity, when an object has changing velocity (whether increasing or decreasing), the object is known to be under some acceleration or deceleration respectively.
Acceleration
The acceleration in a body is defined as the rate of change of velocity with respect to time. When the object has no acceleration, it has constant velocity, and when the object has some positive or negative value of acceleration, the body has varied velocity, In such a case, the concept of initial and final velocities are introduced. The equations of motion are applicable for objects undergoing constant acceleration. Although, it is not easy to find an object with constant acceleration in real life, there are still some practical examples. For instance, when a ball is dropped (assume no air resistance), it experiences a constant acceleration due to gravity.
Equations of Motion
Equations of motion were given by Newton. Equations of motion were introduced to define all the unknown possible parameters of a body in motion undergoing some constant acceleration. If all three equations are known, all types of problems can be solved since these three equations cover all parameters.
Newton’s First Equation of Motion
Let the initial velocity be u, final velocity be v, acceleration of the object be a, and the time be t. The first equation of motion will be,
v = u + at
Proof:
a = (v-u)/t
at = v-u
v = u+ at
Newton’s Second Equation of motion
Let the initial velocity of the object be u, acceleration of the object be a, and the displacement covered by the object be S, the second equation will be,
S = ut + 1/2(at2)
Proof:
The average velocity is given as- v+u/2
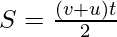
Putting the value of v from first equation of motion here,
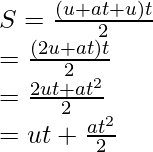
Newton’s Third equation of Motion
Let the initial and final velocities of the object be given as u and v respectively, the acceleration of the object be a, and the displacement covered by the object be given as S. Then, the third equation of motion is given as,
v2 = u2+ 2as
Proof:
The average velocity of an object is ⇢ v+u/2
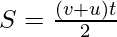
The acceleration of the object can be written as,
a= (v-u)/t
Multiply S and a,
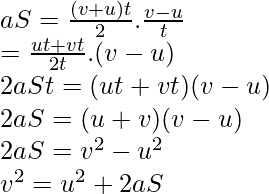
Sample Problems
Question 1: Define Average Speed and Average Velocity?
Answer:
Average Speed
It is defined as the total path covered in total time.
Average Speed= Total Distance/Total Time= D/T
Average Velocity
It is defined as the Total displacement by total time taken.
Average Velocity (v)= S2– S1/ T2– T1 = S/T
Question 2: A Body at rest was accelerated, and it traveled for 5 minutes. The constant acceleration provided to the body was 2 m/sec2. Find the final velocity the object had before coming to a stop. Also, answer the equation of motion used to find out the final velocity.
Solution:
The first equation of motion is the best suitable here to find out the final velocity.
First equation of motion, v=u +at
Initial velocity= 0 m/sec
Time for which object was in motion= 5 minute = 5× 60sec= 300 seconds
The constant acceleration provided to the object= 2 m/sec2
v= u+ at
v= 0+ 2× 300
v= 600m/sec
Question 3: A ball is dropped from a certain height. It took the ball 15 seconds to reach the ground. What is the height at which the ball was initially, also answer which equation of motion is used to answer this question? [Take g=10m/sec2]
Answer:
The second equation of motion is the best suitable for answering this type of question,
Second equation of motion, S= ut + 1/2(at2)
The height at which ball is dropped= h
As the ball is dropped, u= 0 m/sec
a=g (acceleration due to gravity), g= 10m/sec2
h= 0+ 1/2(gt2)
h= 1/2(10× 15×15)
h= 1125meters
The height at which ball was present initially was 1.125kms.
Question 4: What does the statement tells “The Average velocity of a body is equal to the instantaneous velocity”?
Answer:
The statement “The average velocity of a body is equal to its instantaneous velocity” means that there is no variation in the velocity of the object whatsoever throughout its motion.
Hence, it can be concluded from the statement that the body has a constant velocity.
Question 5: A Car with an initial speed of 1 m/sec was in motion for 10 minutes, and then it came to a stop, the velocity right before it stopped was 5 m/sec. What was the constant acceleration of the car?
Solution:
Initial Velocity= 1 m/sec
Final Velocity= 5 m/sec
Time for which the car was in motion = 10 mint
Acceleration = ?
Using First equation of motion,
v = u+ at
5 = 1+ a× (10×60)
a × 600 = 4
a = 4/600
a = 0.0066 m/sec2
Question 6: A cycle covered 2 km in 8 minutes and the initial velocity of the cycle was 1 m/sec. Find the acceleration that the cycle had in its motion.
Solution:
Displacement covered= 2km
Total Time Taken = 8minutes= 8× 60= 480 seconds.
Initial Velocity= 1 m/sec
Using Second equation of motion to find the acceleration of the cycle,
Second Equation of motion, S= ut + 1/2(at2)
2000= 1× 480 + 1/2(a×4802)
2000= 480+ 115200a
1520= 115200a
a= 0.0139m/sec2
Question 7: A toy is accidentally dropped by a kid from his roof. The final velocity of the toy before it reached the ground was 8m/sec. Find the height of the building.
Solution:
Acceleration of the toy is equal to the acceleration due to gravity.
a = g = 9.8m/sec2
Final velocity= 8m/sec
Initial velocity= 0m/sec
Applying Third equation of motion, v2= u2+ 2aS
82 = 0+ 2×9.8 × S
S = 64/9.8×2
S = 3.26 meters
Hence, the height of the building is 3.26 meters.
Question 8: Can an object having varied acceleration will be considered a good example for equations of motion?
Answer:
No. The equations of motion are applicable only for the body undergoing constant acceleration. Acceleration changing with respect to time is called as jerk and a body undergoing jerk will not be suitable in the equations of motion.
Question 9: Find the final velocity of an object that traveled a distance of 500meter with an initial speed of 2m/sec and acceleration of the object was 0.5m/sec2.
Solution:
The third equation of motion is suitable for this example,
Third equation of motion, v2= u2+2aS
v= ?, u=2m/sec, a=0.5m/sec2, S= 500m
v2= 25+2× 0.5 × 500
v2= 504
v= 22.4m/sec
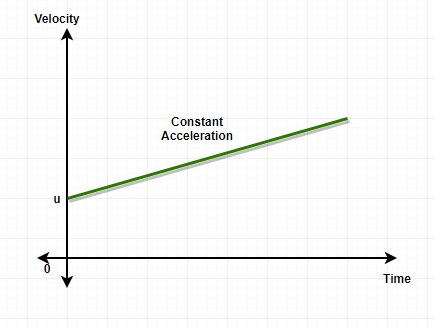
Question 10: Draw the velocity-time graph for zero acceleration and constant acceleration.
Answer:
The slope for zero acceleration on velocity time graph is zero and hence the graph is parallel to x-axis.

The slope for constant acceleration will have a constant value on velocity time graph and hence, the graph will be a straight line.
Share your thoughts in the comments
Please Login to comment...