What is the least number by which 8640 is divided so that the quotient is a complete cube number?
Last Updated :
12 Jan, 2023
A number system is a method of showing numbers by writing, which is a mathematical way of representing the numbers of a given set, by using the numbers or symbols in a mathematical manner. The writing system for denoting numbers using digits or symbols in a logical manner is defined as a number system, which Represents a useful set of numbers also Reflects the arithmetic and algebraic structure of a number, and Provides standard representation.
Prime Factorization
It is a process of factoring a number in terms of prime numbers i.e. the factors will be prime numbers. Here are some of the prime factorization concepts,
First, the simplest algorithm to find the prime factors of a number is to keep on dividing the original number by prime factors until we get the remainder equal to 1. For example, prime factorizing the number 70 we get, 70/2 =35 , 35/5 = 7, 7/7 = 1. Since we received the remainder, it cannot be further factorized. Therefore, 70 = 2 x 5 x 7, where 2, 5 and 7 are prime factors. There are few prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, and so on. These prime numbers when multiplied with any of the natural numbers produce composite numbers.
Prime Factorization Method
Prime factorization is a way of showing a number as a product of its prime factors. A prime number is a number that has exactly two factors, 1 and the number itself. It is also defined as a way of finding the prime factors of a number, such that the original number is evenly divisible by these factors. As we all know, a composite number has more than two factors, therefore, this method is applicable only for composite numbers and not for prime numbers. For example, here the prime factors of 126 will be 2, 3, and 7 as 2 × 3 × 3 × 7 = 126, and 2, 3, 7 are prime numbers. An example of the number 40 is 5 × 8, but 8 is not a prime number. The number 8 is expressed as 2 ×2 × 2 since 5 and 2 are prime numbers. Therefore, the prime factorization of 40 is 2 × 2 × 2 × 5 = 23 × 5.
Some of the commonly used prime factorization methods
Division Method
Steps to calculate the prime factors of a number is similar to the process of finding the factors of a large number. Follow the below steps to find the prime factors of a number using the division method: Some of the steps are
- First, find the smallest prime number that exactly divides the given number.
- Then, repeat the same for quotient i.e. divide the quotient by the smallest prime number.
- Repeat the above steps until the quotient becomes 1.
- Multiply all the prime factors.
Question: Do the prime factorization of 460.
Solution:
Detailed step-by-step process of prime factorization by taking 460.
Step 1: Divide 460 by the least prime number i.e. 2.
So, 460 ÷ 2 = 230
Step 2: Again Divide 230 with the least prime number (which is again 2).
230 ÷ 2 = 115
Step 3: Divide again with the least prime number which will be 5.
115 ÷ 5 = 23
Step 4: As 23 is a prime number, divide it by itself to get 1.
Now, the prime factors of 460 will be 22 × 5 × 23
Factor Tree Method
In this method, the factors of a number are found and then those numbers are further factorized until we reach the prime numbers. For the evaluation of the prime factorization of a number using the factor tree method, here are the steps given below:
- The top of the factor tree is considered the root of the tree.
- Make the corresponding pair of factors as the branches of the tree.
- Factorize the composite factors that are found in step 2, and make the pair of factors as the next branches of the tree.
- Repeat step 3 to get the prime factors of all the composite factors.
Question: What is the prime factorization of 70 and 300 using the Factor tree method?
Solution:
Number 70 is first factorized into two numbers i.e. 7 and 10. Again, 7 and 10 is factorized to get the prime factors of 7 and 10, such that; 7 is 7, and 10 = 2 × 5
So we can write the prime factors of 70 altogether, then;
70 = 7 × 10
= 7 × 2 × 5
So prime factors of 70 are 7 × 2 × 5
The same is the second case for number 300, such as;
300 = 2 × 150
= 2 × 15 × 10 and further once again
= 2 × 3 × 5 × 2 × 5
= 22 × 3 × 52 are the prime factors of 300
So in both above cases, a tree structure is formed,

PRIME FACTORS OF 70 AND 300 BY FACTOR TREE METHOD
What is the least number by which 8640 is divided, the quotient as a complete cube number?
Solution:
The prime factorization method is seen to be the easiest method of finding the factors, let’s use the prime factorization method to find the least number.

8640 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 × 5
= 23 × 23 × 33 × 5
here, there is triplet of 2 and 3 but there is no triplet of 5 .. so, we can say here 5 occurs as a prime number only once. According to prime factorization method here 5 is the smallest number by which 8640 must be divided so that the quotient is a perfect cube.
Similar Problems
Question 1: Find the least number by which 7803 is divided, the quotient as a complete cube number?
Solution:
To find the least number by which 7803 is divided, the quotient as a complete cube number, use the prime factorization division method to find the least number.
Write as 7803 = 3 × 3 × 3 × 17 × 17
= 33 × 172
Here you can see 7803 is not a perfect square as you can see in attached image :

Divide it by 172 = 289 to make the quotient a perfect cube, which gives us 27 as quotient which is a perfect cube.
So here 289 is the required smallest number.
Question 2: What is the least number by which 107811 is divided, the quotient as a complete cube number?
Solution:
107811 = 3 × 3 × 3 × 3 × 11 × 11 × 11
= 33 × 113 × 3
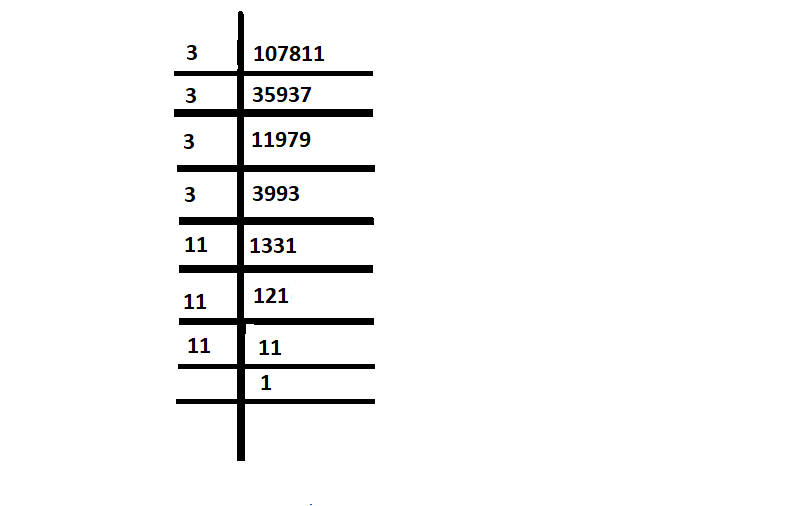
Hence, see 107811 is not a perfect cube.
Divide it by 3 to make the quotient a perfect cube, which gives 35937 as quotient which is a perfect cube.
So here, 3 is the required smallest number.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...