Reverse Level Order Traversal
Last Updated :
17 Apr, 2024
We have discussed the level-order traversal of a tree in the previous post. The idea is to print the last level first, then the second last level, and so on. Like Level order traversal, every level is printed from left to right.
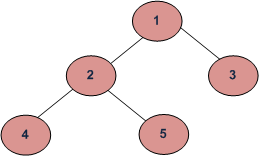
The reverse Level order traversal of the above tree is “4 5 2 3 1”.
Both methods for normal level order traversal can be easily modified to do reverse level order traversal.
METHOD 1 (Recursive function to print a given level)
We can easily modify method 1 of the normal level order traversal. In method 1, we have a method printGivenLevel() which prints a given level number. The only thing we need to change is, instead of calling printGivenLevel() from the first level to the last level, we call it from the last level to the first level.
C++
// A recursive C++ program to print
// REVERSE level order traversal
#include <bits/stdc++.h>
using namespace std;
/* A binary tree node has data,
pointer to left and right child */
class node
{
public:
int data;
node* left;
node* right;
};
/*Function prototypes*/
void printGivenLevel(node* root, int level);
int height(node* node);
node* newNode(int data);
/* Function to print REVERSE
level order traversal a tree*/
void reverseLevelOrder(node* root)
{
int h = height(root);
int i;
for (i=h; i>=1; i--) //THE ONLY LINE DIFFERENT FROM NORMAL LEVEL ORDER
printGivenLevel(root, i);
}
/* Print nodes at a given level */
void printGivenLevel(node* root, int level)
{
if (root == NULL)
return;
if (level == 1)
cout << root->data << " ";
else if (level > 1)
{
printGivenLevel(root->left, level - 1);
printGivenLevel(root->right, level - 1);
}
}
/* Compute the "height" of a tree -- the number of
nodes along the longest path from the root node
down to the farthest leaf node.*/
int height(node* node)
{
if (node == NULL)
return 0;
else
{
/* compute the height of each subtree */
int lheight = height(node->left);
int rheight = height(node->right);
/* use the larger one */
if (lheight > rheight)
return(lheight + 1);
else return(rheight + 1);
}
}
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
node* newNode(int data)
{
node* Node = new node();
Node->data = data;
Node->left = NULL;
Node->right = NULL;
return(Node);
}
/* Driver code*/
int main()
{
node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
cout << "Level Order traversal of binary tree is \n";
reverseLevelOrder(root);
return 0;
}
// This code is contributed by rathbhupendra
// A recursive C program to print REVERSE level order traversal
#include <stdio.h>
#include <stdlib.h>
/* A binary tree node has data, pointer to left and right child */
struct node
{
int data;
struct node* left;
struct node* right;
};
/*Function prototypes*/
void printGivenLevel(struct node* root, int level);
int height(struct node* node);
struct node* newNode(int data);
/* Function to print REVERSE level order traversal a tree*/
void reverseLevelOrder(struct node* root)
{
int h = height(root);
int i;
for (i=h; i>=1; i--) //THE ONLY LINE DIFFERENT FROM NORMAL LEVEL ORDER
printGivenLevel(root, i);
}
/* Print nodes at a given level */
void printGivenLevel(struct node* root, int level)
{
if (root == NULL)
return;
if (level == 1)
printf("%d ", root->data);
else if (level > 1)
{
printGivenLevel(root->left, level-1);
printGivenLevel(root->right, level-1);
}
}
/* Compute the "height" of a tree -- the number of
nodes along the longest path from the root node
down to the farthest leaf node.*/
int height(struct node* node)
{
if (node==NULL)
return 0;
else
{
/* compute the height of each subtree */
int lheight = height(node->left);
int rheight = height(node->right);
/* use the larger one */
if (lheight > rheight)
return(lheight+1);
else return(rheight+1);
}
}
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
struct node* newNode(int data)
{
struct node* node = (struct node*)
malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return(node);
}
/* Driver program to test above functions*/
int main()
{
struct node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
printf("Level Order traversal of binary tree is \n");
reverseLevelOrder(root);
return 0;
}
// A recursive java program to print reverse level order traversal
// A binary tree node
class Node
{
int data;
Node left, right;
Node(int item)
{
data = item;
left = right;
}
}
class BinaryTree
{
Node root;
/* Function to print REVERSE level order traversal a tree*/
void reverseLevelOrder(Node node)
{
int h = height(node);
int i;
for (i = h; i >= 1; i--)
//THE ONLY LINE DIFFERENT FROM NORMAL LEVEL ORDER
{
printGivenLevel(node, i);
}
}
/* Print nodes at a given level */
void printGivenLevel(Node node, int level)
{
if (node == null)
return;
if (level == 1)
System.out.print(node.data + " ");
else if (level > 1)
{
printGivenLevel(node.left, level - 1);
printGivenLevel(node.right, level - 1);
}
}
/* Compute the "height" of a tree -- the number of
nodes along the longest path from the root node
down to the farthest leaf node.*/
int height(Node node)
{
if (node == null)
return 0;
else
{
/* compute the height of each subtree */
int lheight = height(node.left);
int rheight = height(node.right);
/* use the larger one */
if (lheight > rheight)
return (lheight + 1);
else
return (rheight + 1);
}
}
// Driver program to test above functions
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
// Let us create trees shown in above diagram
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
System.out.println("Level Order traversal of binary tree is : ");
tree.reverseLevelOrder(tree.root);
}
}
// This code has been contributed by Mayank Jaiswal
# A recursive Python program to print REVERSE level order traversal
# A binary tree node
class Node:
# Constructor to create a new node
def __init__(self, data):
self.data = data
self.left = None
self.right = None
# Function to print reverse level order traversal
def reverseLevelOrder(root):
h = height(root)
for i in reversed(range(1, h+1)):
printGivenLevel(root,i)
# Print nodes at a given level
def printGivenLevel(root, level):
if root is None:
return
if level ==1 :
print root.data,
elif level>1:
printGivenLevel(root.left, level-1)
printGivenLevel(root.right, level-1)
# Compute the height of a tree-- the number of
# nodes along the longest path from the root node
# down to the farthest leaf node
def height(node):
if node is None:
return 0
else:
# Compute the height of each subtree
lheight = height(node.left)
rheight = height(node.right)
# Use the larger one
if lheight > rheight :
return lheight + 1
else:
return rheight + 1
# Driver program to test above function
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
print "Level Order traversal of binary tree is"
reverseLevelOrder(root)
# This code is contributed by Nikhil Kumar Singh(nickzuck_007)
// A recursive C# program to print
// reverse level order traversal
using System;
// A binary tree node
class Node
{
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = right;
}
}
class BinaryTree
{
Node root;
/* Function to print REVERSE
level order traversal a tree*/
void reverseLevelOrder(Node node)
{
int h = height(node);
int i;
for (i = h; i >= 1; i--)
// THE ONLY LINE DIFFERENT
// FROM NORMAL LEVEL ORDER
{
printGivenLevel(node, i);
}
}
/* Print nodes at a given level */
void printGivenLevel(Node node, int level)
{
if (node == null)
return;
if (level == 1)
Console.Write(node.data + " ");
else if (level > 1)
{
printGivenLevel(node.left, level - 1);
printGivenLevel(node.right, level - 1);
}
}
/* Compute the "height" of a tree --
the number of nodes along the longest
path from the root node down to the
farthest leaf node.*/
int height(Node node)
{
if (node == null)
return 0;
else
{
/* compute the height of each subtree */
int lheight = height(node.left);
int rheight = height(node.right);
/* use the larger one */
if (lheight > rheight)
return (lheight + 1);
else
return (rheight + 1);
}
}
// Driver Code
static public void Main(String []args)
{
BinaryTree tree = new BinaryTree();
// Let us create trees shown
// in above diagram
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
Console.WriteLine("Level Order traversal " +
"of binary tree is : ");
tree.reverseLevelOrder(tree.root);
}
}
// This code is contributed
// by Arnab Kundu
<script>
// A recursive JavaScript program to print
// reverse level order traversal
// A binary tree node
class Node {
constructor(item) {
this.data = item;
this.left = null;
this.right = null;
}
}
class BinaryTree {
constructor() {
this.root = null;
}
/* Function to print REVERSE
level order traversal a tree*/
reverseLevelOrder(node) {
var h = this.height(node);
var i;
for (
i = h;
i >= 1;
i-- // THE ONLY LINE DIFFERENT // FROM NORMAL LEVEL ORDER
) {
this.printGivenLevel(node, i);
}
}
/* Print nodes at a given level */
printGivenLevel(node, level) {
if (node == null) return;
if (level == 1) document.write(node.data + " ");
else if (level > 1) {
this.printGivenLevel(node.left, level - 1);
this.printGivenLevel(node.right, level - 1);
}
}
/* Compute the "height" of a tree --
the number of nodes along the longest
path from the root node down to the
farthest leaf node.*/
height(node) {
if (node == null) return 0;
else {
/* compute the height of each subtree */
var lheight = this.height(node.left);
var rheight = this.height(node.right);
/* use the larger one */
if (lheight > rheight) return lheight + 1;
else return rheight + 1;
}
}
}
// Driver Code
var tree = new BinaryTree();
// Let us create trees shown
// in above diagram
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
document.write(
"Level Order traversal " + "of binary tree is : <br>"
);
tree.reverseLevelOrder(tree.root);
</script>
OutputLevel Order traversal of binary tree is
4 5 2 3 1
Time Complexity: O(n^2)
Auxiliary Space: O(h), where h is the height of the tree, this space is due to the recursive call stack.
METHOD 2 (Using Queue and Stack)
The idea is to use a deque(double-ended queue) to get the reverse level order. A deque allows insertion and deletion at both ends. If we do normal level order traversal and instead of printing a node, push the node to a stack and then print the contents of the deque, we get “5 4 3 2 1” for the above example tree, but the output should be “4 5 2 3 1”. So to get the correct sequence (left to right at every level), we process the children of a node in reverse order, we first push the right subtree to the deque, then process the left subtree.
C++
// A C++ program to print REVERSE level order traversal using stack and queue
// This approach is adopted from following link
// http://tech-queries.blogspot.in/2008/12/level-order-tree-traversal-in-reverse.html
#include <bits/stdc++.h>
using namespace std;
/* A binary tree node has data, pointer to left and right children */
struct node
{
int data;
struct node* left;
struct node* right;
};
/* Given a binary tree, print its nodes in reverse level order */
void reverseLevelOrder(node* root)
{
stack <node *> S;
queue <node *> Q;
Q.push(root);
// Do something like normal level order traversal order. Following are the
// differences with normal level order traversal
// 1) Instead of printing a node, we push the node to stack
// 2) Right subtree is visited before left subtree
while (Q.empty() == false)
{
/* Dequeue node and make it root */
root = Q.front();
Q.pop();
S.push(root);
/* Enqueue right child */
if (root->right)
Q.push(root->right); // NOTE: RIGHT CHILD IS ENQUEUED BEFORE LEFT
/* Enqueue left child */
if (root->left)
Q.push(root->left);
}
// Now pop all items from stack one by one and print them
while (S.empty() == false)
{
root = S.top();
cout << root->data << " ";
S.pop();
}
}
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
node* newNode(int data)
{
node* temp = new node;
temp->data = data;
temp->left = NULL;
temp->right = NULL;
return (temp);
}
/* Driver program to test above functions*/
int main()
{
struct node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
root->right->right = newNode(7);
cout << "Level Order traversal of binary tree is \n";
reverseLevelOrder(root);
return 0;
}
// A recursive java program to print reverse level order traversal
// using stack and queue
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;
/* A binary tree node has data, pointer to left and right children */
class Node
{
int data;
Node left, right;
Node(int item)
{
data = item;
left = right;
}
}
class BinaryTree
{
Node root;
/* Given a binary tree, print its nodes in reverse level order */
void reverseLevelOrder(Node node)
{
Stack<Node> S = new Stack();
Queue<Node> Q = new LinkedList();
Q.add(node);
// Do something like normal level order traversal order.Following
// are the differences with normal level order traversal
// 1) Instead of printing a node, we push the node to stack
// 2) Right subtree is visited before left subtree
while (Q.isEmpty() == false)
{
/* Dequeue node and make it root */
node = Q.peek();
Q.remove();
S.push(node);
/* Enqueue right child */
if (node.right != null)
// NOTE: RIGHT CHILD IS ENQUEUED BEFORE LEFT
Q.add(node.right);
/* Enqueue left child */
if (node.left != null)
Q.add(node.left);
}
// Now pop all items from stack one by one and print them
while (S.empty() == false)
{
node = S.peek();
System.out.print(node.data + " ");
S.pop();
}
}
// Driver program to test above functions
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
// Let us create trees shown in above diagram
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.right.left = new Node(6);
tree.root.right.right = new Node(7);
System.out.println("Level Order traversal of binary tree is :");
tree.reverseLevelOrder(tree.root);
}
}
// This code has been contributed by Mayank Jaiswal
# Python program to print REVERSE level order traversal using
# stack and queue
from collections import deque
# A binary tree node
class Node:
# Constructor to create a new node
def __init__(self, data):
self.data = data
self.left = None
self.right = None
# Given a binary tree, print its nodes in reverse level order
def reverseLevelOrder(root):
# we can use a double ended queue which provides O(1) insert at the beginning
# using the appendleft method
# we do the regular level order traversal but instead of processing the
# left child first we process the right child first and the we process the left child
# of the current Node
# we can do this One pass reduce the space usage not in terms of complexity but intuitively
q = deque()
q.append(root)
ans = deque()
while q:
node = q.popleft()
if node is None:
continue
ans.appendleft(node.data)
if node.right:
q.append(node.right)
if node.left:
q.append(node.left)
return ans
# Driver program to test above function
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)
print "Level Order traversal of binary tree is"
deq = reverseLevelOrder(root)
for key in deq:
print (key),
# This code is contributed by Nikhil Kumar Singh(nickzuck_007)
// A recursive C# program to print reverse
// level order traversal using stack and queue
using System.Collections.Generic;
using System;
/* A binary tree node has data,
pointer to left and right children */
public class Node
{
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = right;
}
}
public class BinaryTree
{
Node root;
/* Given a binary tree, print its
nodes in reverse level order */
void reverseLevelOrder(Node node)
{
Stack<Node> S = new Stack<Node>();
Queue<Node> Q = new Queue<Node>();
Q.Enqueue(node);
// Do something like normal level
// order traversal order.Following
// are the differences with normal
// level order traversal
// 1) Instead of printing a node, we push the node to stack
// 2) Right subtree is visited before left subtree
while (Q.Count>0)
{
/* Dequeue node and make it root */
node = Q.Peek();
Q.Dequeue();
S.Push(node);
/* Enqueue right child */
if (node.right != null)
// NOTE: RIGHT CHILD IS ENQUEUED BEFORE LEFT
Q.Enqueue(node.right);
/* Enqueue left child */
if (node.left != null)
Q.Enqueue(node.left);
}
// Now pop all items from stack
// one by one and print them
while (S.Count>0)
{
node = S.Peek();
Console.Write(node.data + " ");
S.Pop();
}
}
// Driver code
public static void Main()
{
BinaryTree tree = new BinaryTree();
// Let us create trees shown in above diagram
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.right.left = new Node(6);
tree.root.right.right = new Node(7);
Console.WriteLine("Level Order traversal of binary tree is :");
tree.reverseLevelOrder(tree.root);
}
}
/* This code contributed by PrinciRaj1992 */
<script>
// A recursive javascript program to print
// reverse level order traversal
// using stack and queue
/* A binary tree node has data, pointer to left
and right children */
class Node
{
constructor(item)
{
this.data = item;
this.left = this.right=null;
}
}
let root;
/* Given a binary tree, print its nodes in reverse level order */
function reverseLevelOrder(node)
{
let S = [];
let Q = [];
Q.push(node);
// Do something like normal
// level order traversal order.Following
// are the differences with normal
// level order traversal
// 1) Instead of printing a node,
// we push the node to stack
// 2) Right subtree is visited before left subtree
while (Q.length != 0)
{
/* Dequeue node and make it root */
node = Q[0];
Q.shift();
S.push(node);
/* Enqueue right child */
if (node.right != null)
// NOTE: RIGHT CHILD IS ENQUEUED BEFORE LEFT
Q.push(node.right);
/* Enqueue left child */
if (node.left != null)
Q.push(node.left);
}
// Now pop all items from stack
// one by one and print them
while (S.length != 0)
{
node = S.pop();
document.write(node.data + " ");
}
}
// Driver program to test above functions
// Let us create trees shown in above diagram
root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
document.write("Level Order traversal of binary tree is :<br>");
reverseLevelOrder(root);
// This code is contributed by avanitrachhadiya2155
</script>
OutputLevel Order traversal of binary tree is
4 5 6 7 2 3 1
Time Complexity: O(n), where n is the number of nodes in the binary tree.
Auxiliary Space: O(n), for stack and queue.
Method 3: ( Using a Hash_Map)
The basic idea behind this approach is to use a hashmap to store the nodes at each level of the binary tree, and then iterate over the hashmap in reverse order of the levels to obtain the reverse level order traversal.
Follow the steps to implement above idea:
- Define a Node struct to represent a binary tree node.
- Define a recursive function addNodesToMap that takes a binary tree node, a level, and a reference to an unordered map, and adds the node to the vector of nodes at its level in the unordered map. This function should then recursively call itself on the left and right subtrees.
- Define the main reverseLevelOrder function that takes the root of the binary tree as input, and returns a vector containing the nodes in reverse level order.
- Inside the reverseLevelOrder function, create an unordered map to store the nodes at each level of the binary tree.
- Call the addNodesToMap function on the root of the binary tree, with level 0 and a reference to the unordered map, to populate the map with nodes.
- Iterate over the unordered map in reverse order of the levels, and add the nodes to the result vector in the order they appear in the vectors in the unordered map.
- Return the result vector containing the nodes in reverse level order.
Below is the implementation:
C++
// C++ code to implement the hash_map approach
#include <bits/stdc++.h>
#include <unordered_map>
using namespace std;
// Definition of a binary tree node
struct Node {
int data;
Node* left;
Node* right;
Node(int val)
{
data = val;
left = right = nullptr;
}
};
// Recursive function to traverse the binary
// tree and add nodes to the hashmap
void addNodesToMap(
Node* node, int level,
unordered_map<int, vector<int> >& nodeMap)
{
if (node == nullptr) {
return;
}
// Add the current node to the vector of
// nodes at its level in the hashmap
nodeMap[level].push_back(node->data);
// Recursively traverse the left and
// right subtrees
addNodesToMap(node->left, level + 1, nodeMap);
addNodesToMap(node->right, level + 1, nodeMap);
}
vector<int> reverseLevelOrder(Node* root)
{
vector<int> result;
// Create an unordered_map to store the
// nodes at each level of the binary tree
unordered_map<int, vector<int> > nodeMap;
// Traverse the binary tree recursively and
// add nodes to the hashmap
addNodesToMap(root, 0, nodeMap);
// Iterate over the hashmap in reverse order of the
// levels and add nodes to the result vector
for (int level = nodeMap.size() - 1; level >= 0;
level--) {
vector<int> nodesAtLevel = nodeMap[level];
for (int i = 0; i < nodesAtLevel.size(); i++) {
result.push_back(nodesAtLevel[i]);
}
}
return result;
}
// Driver code
int main()
{
// Create the binary tree
Node* root = new Node(10);
root->left = new Node(20);
root->right = new Node(30);
root->left->left = new Node(40);
root->left->right = new Node(60);
// Find the reverse level order traversal
// of the binary tree
vector<int> result = reverseLevelOrder(root);
cout << "Level Order traversal of binary tree is:"
<< endl;
// Print the result
for (int i = 0; i < result.size(); i++) {
cout << result[i] << " ";
}
cout << endl;
return 0;
}
//This code is contributed by Veerendra_Singh_Rajpoot
import java.util.*;
// Definition of a binary tree node
class Node {
int data;
Node left;
Node right;
Node(int val) {
data = val;
left = right = null;
}
}
class Main {
// Recursive function to traverse the binary
// tree and add nodes to the hashmap
static void addNodesToMap(Node node, int level, Map<Integer, List<Integer>> nodeMap) {
if (node == null) {
return;
}
// Add the current node to the list of
// nodes at its level in the hashmap
if (!nodeMap.containsKey(level)) {
nodeMap.put(level, new ArrayList<>());
}
nodeMap.get(level).add(node.data);
// Recursively traverse the left and
// right subtrees
addNodesToMap(node.left, level + 1, nodeMap);
addNodesToMap(node.right, level + 1, nodeMap);
}
static List<Integer> reverseLevelOrder(Node root) {
List<Integer> result = new ArrayList<>();
// Create a map to store the nodes at each level of the binary tree
Map<Integer, List<Integer>> nodeMap = new HashMap<>();
// Traverse the binary tree recursively and
// add nodes to the hashmap
addNodesToMap(root, 0, nodeMap);
// Iterate over the hashmap in reverse order of the
// levels and add nodes to the result list
for (int level = nodeMap.size() - 1; level >= 0; level--) {
List<Integer> nodesAtLevel = nodeMap.get(level);
for (int i = 0; i < nodesAtLevel.size(); i++) {
result.add(nodesAtLevel.get(i));
}
}
return result;
}
// Driver code
public static void main(String[] args) {
// Create the binary tree
Node root = new Node(10);
root.left = new Node(20);
root.right = new Node(30);
root.left.left = new Node(40);
root.left.right = new Node(60);
// Find the reverse level order traversal
// of the binary tree
List<Integer> result = reverseLevelOrder(root);
System.out.println("Level Order traversal of binary tree is:");
// Print the result
for (int i = 0; i < result.size(); i++) {
System.out.print(result.get(i) + " ");
}
System.out.println();
}
}
// This code is contributed by Veerendra_Singh_Rajpoot
class Node:
def __init__(self, val):
self.data = val
self.left = None
self.right = None
# Recursive function to traverse the binary
def addNodesToMap(node, level, nodeMap):
if node is None:
return
if level in nodeMap:
nodeMap[level].append(node.data)
else:
nodeMap[level] = [node.data]
# Recursively traverse the left and right subtrees
addNodesToMap(node.left, level + 1, nodeMap)
addNodesToMap(node.right, level + 1, nodeMap)
def GFG(root):
result = []
nodeMap = {}
# Traverse the binary tree recursively
addNodesToMap(root, 0, nodeMap)
# Iterate over the dictionary in reverse order
for level in range(len(nodeMap) - 1, -1, -1):
nodesAtLevel = nodeMap[level]
result.extend(nodesAtLevel)
return result
# Driver code
if __name__ == "__main__":
# Create the binary tree
root = Node(10)
root.left = Node(20)
root.right = Node(30)
root.left.left = Node(40)
root.left.right = Node(60)
# Find the reverse level order traversal of the binary tree
result = GFG(root)
print("Level Order traversal of binary tree is:")
# Print the result without brackets
print(" ".join(map(str, result)))
using System;
using System.Collections.Generic;
// Definition of a binary tree node
class Node {
public int data;
public Node left;
public Node right;
public Node(int val)
{
data = val;
left = right = null;
}
}
class Program {
// Recursive function to traverse the binary
// tree and add nodes to the hashmap
static void
AddNodesToMap(Node node, int level,
Dictionary<int, List<int> > nodeMap)
{
if (node == null) {
return;
}
// Add the current node to the list of
// nodes at its level in the hashmap
if (!nodeMap.ContainsKey(level)) {
nodeMap[level] = new List<int>();
}
nodeMap[level].Add(node.data);
// Recursively traverse the left and
// right subtrees
AddNodesToMap(node.left, level + 1, nodeMap);
AddNodesToMap(node.right, level + 1, nodeMap);
}
static List<int> ReverseLevelOrder(Node root)
{
List<int> result = new List<int>();
// Create a dictionary to store the
// nodes at each level of the binary tree
Dictionary<int, List<int> > nodeMap
= new Dictionary<int, List<int> >();
// Traverse the binary tree recursively and
// add nodes to the dictionary
AddNodesToMap(root, 0, nodeMap);
// Iterate over the dictionary in reverse order of
// the levels and add nodes to the result list
for (int level = nodeMap.Count - 1; level >= 0;
level--) {
List<int> nodesAtLevel = nodeMap[level];
for (int i = 0; i < nodesAtLevel.Count; i++) {
result.Add(nodesAtLevel[i]);
}
}
return result;
}
// Driver code
static void Main()
{
// Create the binary tree
Node root = new Node(10);
root.left = new Node(20);
root.right = new Node(30);
root.left.left = new Node(40);
root.left.right = new Node(60);
// Find the reverse level order traversal
// of the binary tree
List<int> result = ReverseLevelOrder(root);
Console.WriteLine(
"Level Order traversal of binary tree is:");
// Print the result
foreach(int val in result)
{
Console.Write(val + " ");
}
Console.WriteLine();
}
}
// Definition of a binary tree node
class Node {
constructor(val) {
this.data = val;
this.left = null;
this.right = null;
}
}
// Recursive function to traverse the binary
// tree and add nodes to the hashmap
function addNodesToMap(node, level, nodeMap) {
if (node === null) {
return;
}
// Add the current node to the vector of
// nodes at its level in the hashmap
if (!nodeMap[level]) {
nodeMap[level] = [];
}
nodeMap[level].push(node.data);
// Recursively traverse the left and
// right subtrees
addNodesToMap(node.left, level + 1, nodeMap);
addNodesToMap(node.right, level + 1, nodeMap);
}
function reverseLevelOrder(root) {
const result = [];
// Create an object to store the nodes at each level of the binary tree
const nodeMap = {};
// Traverse the binary tree recursively and
// add nodes to the hashmap
addNodesToMap(root, 0, nodeMap);
// Iterate over the hashmap in reverse order of the
// levels and add nodes to the result array
const levels = Object.keys(nodeMap).map(Number);
levels.sort((a, b) => b - a); // Sort levels in reverse order
for (const level of levels) {
result.push(...nodeMap[level]);
}
return result;
}
// Driver code
// Create the binary tree
const root = new Node(10);
root.left = new Node(20);
root.right = new Node(30);
root.left.left = new Node(40);
root.left.right = new Node(60);
// Find the reverse level order traversal
// of the binary tree
const result = reverseLevelOrder(root);
console.log("Level Order traversal of binary tree is:");
// Print the result
console.log(result.join(" "));
// This code is contributed by Veerendra_Singh_Rajpoot
OutputLevel Order traversal of binary tree is:
40 60 20 30 10
Time complexity: O(n) – where n is the number of nodes in the binary tree.
Auxiliary Space: O(n) – where n is the number of nodes in the binary tree.
Method 4: Using One Queue
The idea here is to traverse the tree level by level using a single queue. However, we need to modify the way we process nodes at each level to achieve reverse level order traversal.
Follow the steps to implement above idea:
- Start by enqueuing the root node.
- While the queue is not empty, perform the following steps:
- Enqueue all the children of the nodes in the queue (if they exist) from right to left.
- Dequeue a node from the front of the queue and push it onto a stack.
- Once the queue is empty, pop nodes from the stack and collect them in the result vector.
This approach ensures that nodes at each level are processed from right to left, thereby achieving reverse level order traversal.
Below is the implementation:
C++
#include <iostream>
#include <queue>
#include <stack>
#include <vector>
using namespace std;
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
vector<int> reverseLevelOrder(TreeNode* root) {
vector<int> result;
if (root == nullptr)
return result;
queue<TreeNode*> q;
stack<TreeNode*> s;
q.push(root);
while (!q.empty()) {
TreeNode* node = q.front();
q.pop();
// Push the node onto the stack
s.push(node);
// Enqueue right child first if exists
if (node->right)
q.push(node->right);
// Enqueue left child if exists
if (node->left)
q.push(node->left);
}
// Pop nodes from stack and collect them in the result vector
while (!s.empty()) {
result.push_back(s.top()->val);
s.pop();
}
return result;
}
int main() {
// Example usage
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
vector<int> result = reverseLevelOrder(root);
// Print the result
for (int val : result) {
cout << val << " ";
}
// Clean up memory (not shown in the original method)
delete root->left->left;
delete root->left->right;
delete root->left;
delete root->right;
delete root;
return 0;
}
#include <stdio.h>
#include <stdlib.h>
// Define the structure of a binary tree node
struct TreeNode {
int val;
struct TreeNode* left;
struct TreeNode* right;
};
// Function to create a new node
struct TreeNode* newNode(int val) {
struct TreeNode* node = (struct TreeNode*)malloc(sizeof(struct TreeNode));
node->val = val;
node->left = NULL;
node->right = NULL;
return node;
}
// Function to perform reverse level order traversal
int* reverseLevelOrder(struct TreeNode* root, int* returnSize) {
if (root == NULL) {
*returnSize = 0;
return NULL;
}
// Allocate memory for the result array
int* result = (int*)malloc(1000 * sizeof(int));
int idx = 0;
// Create a queue and a stack for traversal
struct TreeNode* queue[1000];
int front = 0, rear = -1;
struct TreeNode* stack[1000];
int top = -1;
// Enqueue the root node
queue[++rear] = root;
// Perform level order traversal
while (front <= rear) {
struct TreeNode* node = queue[front++];
// Push the node onto the stack
stack[++top] = node;
// Enqueue right child first if exists
if (node->right)
queue[++rear] = node->right;
// Enqueue left child if exists
if (node->left)
queue[++rear] = node->left;
}
// Pop nodes from the stack and collect their values in the result array
while (top >= 0) {
result[idx++] = stack[top--]->val;
}
// Set the size of the result array
*returnSize = idx;
return result;
}
int main() {
// Example usage
struct TreeNode* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
int returnSize;
int* result = reverseLevelOrder(root, &returnSize);
// Print the result
for (int i = 0; i < returnSize; i++) {
printf("%d ", result[i]);
}
// Free dynamically allocated memory
free(result);
free(root->left->left);
free(root->left->right);
free(root->left);
free(root->right);
free(root);
return 0;
}
import java.util.*;
class TreeNode {
int val;
TreeNode left, right;
TreeNode(int x) {
val = x;
left = right = null;
}
}
public class ReverseLevelOrder {
public List<Integer> reverseLevelOrder(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null)
return result;
Queue<TreeNode> queue = new LinkedList<>();
Stack<TreeNode> stack = new Stack<>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
// Push the node onto the stack
stack.push(node);
// Enqueue right child first if exists
if (node.right != null)
queue.offer(node.right);
// Enqueue left child if exists
if (node.left != null)
queue.offer(node.left);
}
// Pop nodes from stack and collect them in the result list
while (!stack.isEmpty()) {
result.add(stack.pop().val);
}
return result;
}
public static void main(String[] args) {
// Example usage
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
ReverseLevelOrder solution = new ReverseLevelOrder();
List<Integer> result = solution.reverseLevelOrder(root);
// Print the result
for (int val : result) {
System.out.print(val + " ");
}
}
}
from collections import deque
class TreeNode:
def __init__(self, val):
self.val = val
self.left = None
self.right = None
def reverse_level_order(root):
result = []
if not root:
return result
queue = deque()
stack = []
queue.append(root)
while queue:
node = queue.popleft()
# Push the node onto the stack
stack.append(node)
# Enqueue right child first if exists
if node.right:
queue.append(node.right)
# Enqueue left child if exists
if node.left:
queue.append(node.left)
# Pop nodes from stack and collect their values in the result list
while stack:
result.append(stack.pop().val)
return result
# Example usage
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
result = reverse_level_order(root)
# Print the result
print(*result)
using System;
using System.Collections.Generic;
public class TreeNode {
public int val;
public TreeNode left, right;
public TreeNode(int x) {
val = x;
left = right = null;
}
}
public class ReverseLevelOrder {
public List<int> ReverseLevelOrderTraversal(TreeNode root) {
List<int> result = new List<int>();
if (root == null)
return result;
Queue<TreeNode> queue = new Queue<TreeNode>();
Stack<TreeNode> stack = new Stack<TreeNode>();
queue.Enqueue(root);
while (queue.Count > 0) {
TreeNode node = queue.Dequeue();
// Push the node onto the stack
stack.Push(node);
// Enqueue right child first if exists
if (node.right != null)
queue.Enqueue(node.right);
// Enqueue left child if exists
if (node.left != null)
queue.Enqueue(node.left);
}
// Pop nodes from stack and collect their values in the result list
while (stack.Count > 0) {
result.Add(stack.Pop().val);
}
return result;
}
public static void Main(string[] args) {
// Example usage
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
ReverseLevelOrder solution = new ReverseLevelOrder();
List<int> result = solution.ReverseLevelOrderTraversal(root);
// Print the result
foreach (int val in result) {
Console.Write(val + " ");
}
}
}
class TreeNode {
constructor(val) {
this.val = val;
this.left = null;
this.right = null;
}
}
function reverseLevelOrder(root) {
const result = [];
if (!root)
return result;
const queue = [];
const stack = [];
queue.push(root);
while (queue.length > 0) {
const node = queue.shift();
// Push the node onto the stack
stack.push(node);
// Enqueue right child first if exists
if (node.right)
queue.push(node.right);
// Enqueue left child if exists
if (node.left)
queue.push(node.left);
}
// Pop nodes from stack and collect their values in the result array
while (stack.length > 0) {
result.push(stack.pop().val);
}
return result;
}
// Example usage
const root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
const result = reverseLevelOrder(root);
// Print the result
console.log(result.join(" "));
Output:
4 5 2 3 1
Time Complexity: O(n) – where n is the number of nodes in the binary tree.
Auxiliary Space: O(n) – where n is the number of nodes in the binary tree. The space complexity is primarily due to the stack and queue used for traversal, both of which can potentially hold up to all the nodes in the tree in the worst case.
Share your thoughts in the comments
Please Login to comment...