Enumeration of Binary Trees
Last Updated :
26 Oct, 2021
A Binary Tree is labeled if every node is assigned a label and a Binary Tree is unlabelled if nodes are not assigned any label.
Below two are considered same unlabelled trees
o o
/ \ / \
o o o o
Below two are considered different labelled trees
A C
/ \ / \
B C A B
How many different Unlabelled Binary Trees can be there with n nodes?
For n = 1, there is only one tree
o
For n = 2, there are two trees
o o
/ \
o o
For n = 3, there are five trees
o o o o o
/ \ / \ / \
o o o o o o
/ \ \ /
o o o o
The idea is to consider all possible pairs of counts for nodes in left and right subtrees and multiply the counts for a particular pair. Finally, add the results of all pairs.
For example, let T(n) be count for n nodes.
T(0) = 1 [There is only 1 empty tree]
T(1) = 1
T(2) = 2
T(3) = T(0)*T(2) + T(1)*T(1) + T(2)*T(0) = 1*2 + 1*1 + 2*1 = 5
T(4) = T(0)*T(3) + T(1)*T(2) + T(2)*T(1) + T(3)*T(0)
= 1*5 + 1*2 + 2*1 + 5*1
= 14
The above pattern basically represents n’th Catalan Numbers. First few Catalan numbers are 1 1 2 5 14 42 132 429 1430 4862,…
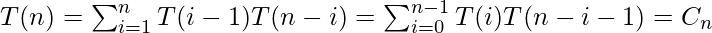
Here,
T(i-1) represents the number of nodes on the left-sub-tree
T(n?i-1) represents the number of nodes on the right-sub-tree
n’th Catalan Number can also be evaluated using the direct formula.
T(n) = (2n)! / (n+1)!n!
The number of Binary Search Trees (BST) with n nodes is also the same as the number of unlabelled trees. The reason for this is simple, in BST also we can make any key a root, If the root is i’th key in sorted order, then i-1 keys can go on one side, and (n-i) keys can go on another side.
How many labeled Binary Trees can be there with n nodes?
To count labeled trees, we can use the above count for unlabelled trees. The idea is simple, every unlabelled tree with n nodes can create n! different labeled trees by assigning different permutations of labels to all nodes.
Therefore,
Number of Labelled Trees = (Number of unlabelled trees) * n!
= [(2n)! / (n+1)!n!] × n!
For example for n = 3, there are 5 * 3! = 5*6 = 30 different labelled trees
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...