Check if a Binary Tree contains duplicate subtrees of size 2 or more
Last Updated :
30 Apr, 2024
Given a Binary Tree, check whether the Binary tree contains a duplicate sub-tree of size 2 or more.
Note: Two same leaf nodes are not considered as the subtree size of a leaf node is one.
Input : Binary Tree
A
/ \
B C
/ \ \
D E B
/ \
D E
Output : Yes
Asked in : Google Interview
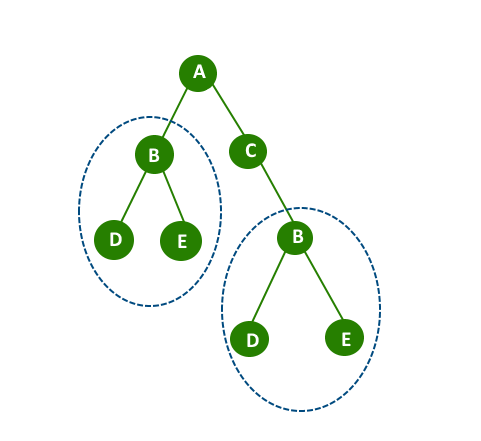
Tree with duplicate Sub-Tree [ highlight by blue color ellipse ]
Method 1 :
A simple solution is that, we pick every node of tree and try to find is any sub-tree of given tree is present in tree which is identical with that sub-tree. Here we can use below post to find if a subtree is present anywhere else in tree.
Check if a binary tree is subtree of another binary tree
[Method 2 ]( Efficient solution )
An Efficient solution based on tree serialization and hashing. The idea is to serialize subtrees as strings and store the strings in hash table. Once we find a serialized tree (which is not a leaf) already existing in hash-table, we return true.
Below The implementation of above idea.
C++
// C++ program to find if there is a duplicate
// sub-tree of size 2 or more.
#include <bits/stdc++.h>
using namespace std;
// Separator node
const char MARKER = '$';
// Structure for a binary tree node
struct Node {
char key;
Node *left, *right;
};
// A utility function to create a new node
Node* newNode(char key)
{
Node* node = new Node;
node->key = key;
node->left = node->right = NULL;
return node;
}
unordered_set<string> subtrees;
// This function returns empty string if tree
// contains a duplicate subtree of size 2 or more.
string dupSubUtil(Node* root)
{
string s = "";
// If current node is NULL, return marker
if (root == NULL)
return s + MARKER;
// If left subtree has a duplicate subtree.
string lStr = dupSubUtil(root->left);
if (lStr.compare(s) == 0)
return s;
// Do same for right subtree
string rStr = dupSubUtil(root->right);
if (rStr.compare(s) == 0)
return s;
// Serialize current subtree
s = s + root->key + lStr + rStr;
// If current subtree already exists in hash
// table. [Note that size of a serialized tree
// with single node is 3 as it has two marker
// nodes.
if (s.length() > 3
&& subtrees.find(s) != subtrees.end())
return "";
subtrees.insert(s);
return s;
}
// Driver program to test above functions
int main()
{
Node* root = newNode('A');
root->left = newNode('B');
root->right = newNode('C');
root->left->left = newNode('D');
root->left->right = newNode('E');
root->right->right = newNode('B');
root->right->right->right = newNode('E');
root->right->right->left = newNode('D');
string str = dupSubUtil(root);
(str.compare("") == 0) ? cout << " Yes "
: cout << " No ";
return 0;
}
// Java program to find if there is a duplicate
// sub-tree of size 2 or more.
import java.util.HashSet;
public class Main {
static char MARKER = '$';
// This function returns empty string if tree
// contains a duplicate subtree of size 2 or more.
public static String
dupSubUtil(Node root, HashSet<String> subtrees)
{
String s = "";
// If current node is NULL, return marker
if (root == null)
return s + MARKER;
// If left subtree has a duplicate subtree.
String lStr = dupSubUtil(root.left, subtrees);
if (lStr.equals(s))
return s;
// Do same for right subtree
String rStr = dupSubUtil(root.right, subtrees);
if (rStr.equals(s))
return s;
// Serialize current subtree
// Append random char in between the value to
// differentiate from 11,1 and 1,11
s = s + root.data + "%" + lStr + "%" + rStr;
// If current subtree already exists in hash
// table. [Note that size of a serialized tree
// with single node is 7 (3+4 accounting for special
// chars appended) as it has two marker nodes.
if (s.length() > 7 && subtrees.contains(s))
return "";
subtrees.add(s);
return s;
}
// Function to find if the Binary Tree contains
// duplicate subtrees of size 2 or more
public static String dupSub(Node root)
{
HashSet<String> subtrees = new HashSet<>();
return dupSubUtil(root, subtrees);
}
public static void main(String args[])
{
Node root = new Node('A');
root.left = new Node('B');
root.right = new Node('C');
root.left.left = new Node('D');
root.left.right = new Node('E');
root.right.right = new Node('B');
root.right.right.right = new Node('E');
root.right.right.left = new Node('D');
String str = dupSub(root);
if (str.equals(""))
System.out.print(" Yes ");
else
System.out.print(" No ");
}
}
// A binary tree Node has data,
// pointer to left child
// and a pointer to right child
class Node {
int data;
Node left, right;
Node(int data) { this.data = data; }
};
// This code is contributed by Gaurav Tiwari
# Structure for a binary tree node
class Node:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
# Separator node
MARKER = '$'
# A utility function to create a new node
def newNode(key):
return Node(key)
subtrees = set()
# This function returns empty string if tree
# contains a duplicate subtree of size 2 or more.
def dupSubUtil(root):
if not root:
return MARKER
# If left subtree has a duplicate subtree.
lStr = dupSubUtil(root.left)
if lStr == "":
return ""
# Do same for right subtree
rStr = dupSubUtil(root.right)
if rStr == "":
return ""
# Serialize current subtree
s = root.key + lStr + rStr
# If current subtree already exists in hash table.
if len(s) > 3 and s in subtrees:
return ""
subtrees.add(s)
return s
# Driver program to test above functions
if __name__ == "__main__":
root = newNode('A')
root.left = newNode('B')
root.right = newNode('C')
root.left.left = newNode('D')
root.left.right = newNode('E')
root.right.right = newNode('B')
root.right.right.right = newNode('E')
root.right.right.left = newNode('D')
str = dupSubUtil(root)
if str == "":
print("Yes")
else:
print("No")
// C# program to find if there is a duplicate
// sub-tree of size 2 or more.
using System;
using System.Collections.Generic;
class GFG
{
static char MARKER = '$';
// This function returns empty string if tree
// contains a duplicate subtree of size 2 or more.
public static String dupSubUtil(Node root,
HashSet<String> subtrees)
{
String s = "";
// If current node is NULL, return marker
if (root == null)
return s + MARKER;
// If left subtree has a duplicate subtree.
String lStr = dupSubUtil(root.left,subtrees);
if (lStr.Equals(s))
return s;
// Do same for right subtree
String rStr = dupSubUtil(root.right,subtrees);
if (rStr.Equals(s))
return s;
// Serialize current subtree
s = s + root.data + lStr + rStr;
// If current subtree already exists in hash
// table. [Note that size of a serialized tree
// with single node is 3 as it has two marker
// nodes.
if (s.Length > 3 && subtrees.Contains(s))
return "";
subtrees.Add(s);
return s;
}
// Function to find if the Binary Tree contains
// duplicate subtrees of size 2 or more
public static String dupSub(Node root)
{
HashSet<String> subtrees = new HashSet<String>();
return dupSubUtil(root,subtrees);
}
// Driver code
public static void Main(String []args)
{
Node root = new Node('A');
root.left = new Node('B');
root.right = new Node('C');
root.left.left = new Node('D');
root.left.right = new Node('E');
root.right.right = new Node('B');
root.right.right.right = new Node('E');
root.right.right.left= new Node('D');
String str = dupSub(root);
if(str.Equals(""))
Console.Write(" Yes ");
else
Console.Write(" No ");
}
}
// A binary tree Node has data,
// pointer to left child
// and a pointer to right child
public class Node
{
public int data;
public Node left,right;
public Node(int data)
{
this.data = data;
}
};
// This code is contributed by 29AjayKumar
// Javascript program to find if there is a duplicate
// sub-tree of size 2 or more.
let MARKER = '$';
// A binary tree Node has data,
// pointer to left child
// and a pointer to right child
class Node {
constructor(data)
{
this.data=data;
}
}
// This function returns empty string if tree
// contains a duplicate subtree of size 2 or more.
function dupSubUtil(root,subtrees)
{
let s = "";
// If current node is NULL, return marker
if (root == null)
return s + MARKER;
// If left subtree has a duplicate subtree.
let lStr = dupSubUtil(root.left,subtrees);
if (lStr==(s))
return s;
// Do same for right subtree
let rStr = dupSubUtil(root.right,subtrees);
if (rStr==(s))
return s;
// Serialize current subtree
s = s + root.data + lStr + rStr;
// If current subtree already exists in hash
// table. [Note that size of a serialized tree
// with single node is 3 as it has two marker
// nodes.
if (s.length > 3 && subtrees.has(s))
return "";
subtrees.add(s);
return s;
}
//Function to find if the Binary Tree contains duplicate
//subtrees of size 2 or more
function dupSub(root)
{
let subtrees=new Set();
return dupSubUtil(root,subtrees);
}
let root = new Node('A');
root.left = new Node('B');
root.right = new Node('C');
root.left.left = new Node('D');
root.left.right = new Node('E');
root.right.right = new Node('B');
root.right.right.right = new Node('E');
root.right.right.left= new Node('D');
let str = dupSub(root);
if(str==(""))
console.log(" Yes ");
else
console.log(" No ");
// This code is contributed by unknown2108
Time Complexity: O(n)
Auxiliary Space: O(n)
Share your thoughts in the comments
Please Login to comment...