Types of Binary Tree

We have discussed Introduction to Binary Tree in set 1 and the Properties of Binary Tree in Set 2. In this post, common types of Binary Trees are discussed. 

Types of Binary Tree based on the number of children:

Following are the types of Binary Tree based on the number of children:

1. Full Binary Tree
2. Degenerate Binary Tree
3. Skewed Binary Trees

1. Full Binary Tree

 A Binary Tree is a full binary tree if every node has 0 or 2 children. The following are examples of a full binary tree. We can also say a full binary tree is a binary tree in which all nodes except leaf nodes have two children. 

A full Binary tree is a special type of binary tree in which every parent node/internal node has either two or no children. It is also known as a proper binary tree.

Full Binary Tree

Program to implement Full Binary tree

C++

#include <iostream>

class Node {
 public:
  int value;
  Node* left;
  Node* right;
  Node(int val) : value(val), left(NULL), right(NULL) {}
};

class FullBinaryTree {
 public:
  Node* root;
  FullBinaryTree() : root(NULL) {}
  void insert(int value) {
    Node* new_node = new Node(value);
    if (!root) {
      root = new_node;
    } else {
      Node* current_node = root;
      while (true) {
        if (!current_node->left) {
          current_node->left = new_node;
          break;
        } else if (!current_node->right) {
          current_node->right = new_node;
          break;
        } else {
          current_node = current_node->left;
        }
      }
    }
  }
};

int main() {
  FullBinaryTree tree;
  tree.insert(1);
  tree.insert(2);
  tree.insert(3);
  tree.insert(4);
  return 0;
}

2. Degenerate (or pathological) tree

A Tree where every internal node has one child. Such trees are performance-wise same as linked list. A degenerate or pathological tree is a tree having a single child either left or right.

Degenerate (or pathological) tree

Program to implement degenerate tree

C++

#include <iostream>
#include <vector>

class Node {
 public:
  int value;
  Node* next;
  Node(int val) : value(val), next(NULL) {}
};

class DegenerateTree {
 public:
  std::vector<Node*> nodes;
  DegenerateTree() {}
  void insert(int value) {
    Node* new_node = new Node(value);
    if (nodes.empty()) {
      nodes.push_back(new_node);
    } else {
      Node* last_node = nodes.back();
      last_node->next = new_node;
      nodes.push_back(new_node);
    }
  }
};

int main() {
  DegenerateTree tree;
  tree.insert(1);
  tree.insert(2);
  tree.insert(3);
  tree.insert(4);
  return 0;
}

3. Skewed Binary Tree

A skewed binary tree is a pathological/degenerate tree in which the tree is either dominated by the left nodes or the right nodes. Thus, there are two types of skewed binary tree: left-skewed binary tree and right-skewed binary tree.

Skewed Binary Tree

Refer to this article to read about more on Skewed Binary Tree

C++

#include <iostream>

class Node {
 public:
  int value;
  Node* right;
  Node(int val) : value(val), right(NULL) {}
};

class SkewedTree {
 public:
  Node* root;
  SkewedTree() : root(NULL) {}
  void insert(int value) {
    Node* new_node = new Node(value);
    if (!root) {
      root = new_node;
    } else {
      Node* current_node = root;
      while (current_node->right) {
        current_node = current_node->right;
      }
      current_node->right = new_node;
    }
  }
};

int main() {
  SkewedTree tree;
  tree.insert(1);
  tree.insert(2);
  tree.insert(3);
  tree.insert(4);
  return 0;
}

Types of Binary Tree On the basis of the completion of levels:

1. Complete Binary Tree
2. Perfect Binary Tree
3. Balanced Binary Tree

1. Complete Binary Tree

 A Binary Tree is a Complete Binary Tree if all the levels are completely filled except possibly the last level and the last level has all keys as left as possible.

A complete binary tree is just like a full binary tree, but with two major differences:

• Every level must be completely filled
• All the leaf elements must lean towards the left.
• The last leaf element might not have a right sibling i.e. a complete binary tree doesn’t have to be a full binary tree.

Complete Binary Tree

Refer to this article to read about more on Complete Tree

2. Perfect Binary Tree

A Binary tree is a Perfect Binary Tree in which all the internal nodes have two children and all leaf nodes are at the same level. 
The following are examples of Perfect Binary Trees. 

A perfect binary tree is a type of binary tree in which every internal node has exactly two child nodes and all the leaf nodes are at the same level.

Perfect Binary Tree

In a Perfect Binary Tree, the number of leaf nodes is the number of internal nodes plus 1   

 L = I + 1 Where L = Number of leaf nodes, I = Number of internal nodes.

A Perfect Binary Tree of height h (where the height of the binary tree is the number of edges in the longest path from the root node to any leaf node in the tree, height of root node is 0) has 2^h+1 – 1 node. 

An example of a Perfect binary tree is ancestors in the family. Keep a person at root, parents as children, parents of parents as their children. 

Refer to this article to read about more on Perfect Tree

3. Balanced Binary Tree

A binary tree is balanced if the height of the tree is O(Log n) where n is the number of nodes. For Example, the AVL tree maintains O(Log n) height by making sure that the difference between the heights of the left and right subtrees is at most 1. Red-Black trees maintain O(Log n) height by making sure that the number of Black nodes on every root to leaf paths is the same and that there are no adjacent red nodes. Balanced Binary Search trees are performance-wise good as they provide O(log n) time for search, insert and delete. 

Example of Balanced and Unbalanced Binary Tree

It is a type of binary tree in which the difference between the height of the left and the right subtree for each node is either 0 or 1. In the figure above, the root node having a value 0 is unbalanced with a depth of 2 units.

Some Special Types of Trees:

On the basis of node values, the Binary Tree can be classified into the following special types:

1. Binary Search Tree
2. AVL Tree
3. Red Black Tree
4. B Tree
5. B+ Tree
6. Segment Tree

Below Image Shows Important Special cases of binary Trees:

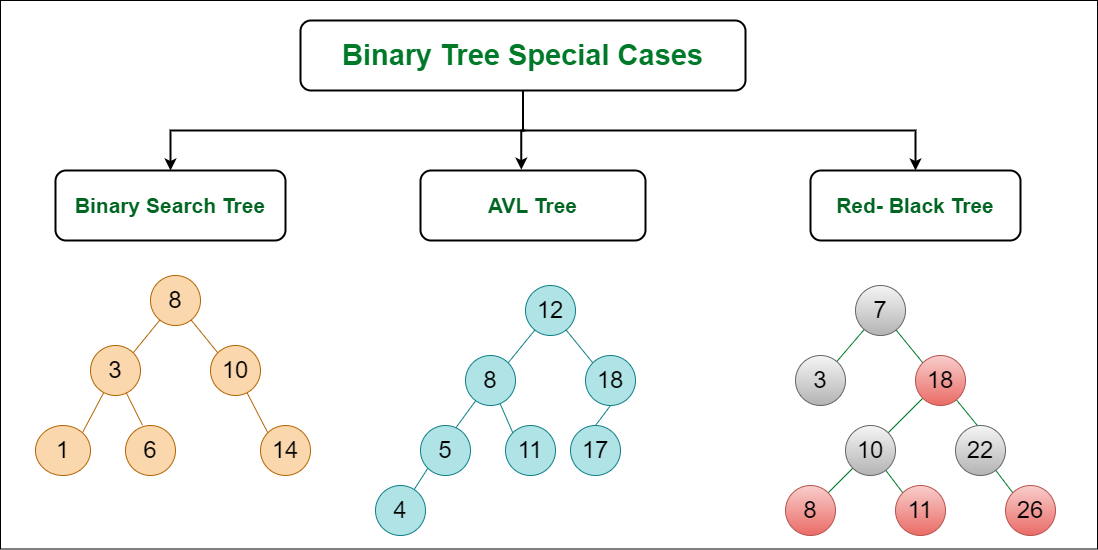
Binary Tree Special cases

1. Binary Search Tree

Binary Search Tree is a node-based binary tree data structure that has the following properties:

• The left subtree of a node contains only nodes with keys lesser than the node’s key.
• The right subtree of a node contains only nodes with keys greater than the node’s key.
• The left and right subtree each must also be a binary search tree.

Binary Search Tree

 2. AVL Tree

AVL tree is a self-balancing Binary Search Tree (BST) where the difference between heights of left and right subtrees cannot be more than one for all nodes. 

Example of AVL Tree shown below: 
The below tree is AVL because the differences between the heights of left and right subtrees for every node are less than or equal to 1

AVL Tree

3. Red Black Tree

A red-black tree is a kind of self-balancing binary search tree where each node has an extra bit, and that bit is often interpreted as the color (red or black). These colors are used to ensure that the tree remains balanced during insertions and deletions. Although the balance of the tree is not perfect, it is good enough to reduce the searching time and maintain it around O(log n) time, where n is the total number of elements in the tree. This tree was invented in 1972 by Rudolf Bayer. 

Red Black Tree

4. B – Tree

B-Tree is a self-balancing search tree. In most of the other self-balancing search trees (like AVL and Red-Black Trees), it is assumed that everything is in the main memory. 
To understand the use of B-Trees, we must think of the huge amount of data that cannot fit in the main memory. When the number of keys is high, the data is read from the disk in the form of blocks. Disk access time is very high compared to the main memory access time. The main idea of using B-Trees is to reduce the number of disk accesses. Most of the tree operations (search, insert, delete, max, min, ..etc ) require O(h) disk accesses where h is the height of the tree. B-tree is a fat tree. The height of B-Trees is kept low by putting the maximum possible keys in a B-Tree node. Generally, the B-Tree node size is kept equal to the disk block size. Since the height of the B-tree is low so total disk accesses for most of the operations are reduced significantly compared to balanced Binary Search Trees like AVL Tree, Red-Black Tree, etc.

Refer to this article to read about more on B-Tree

5. B+ Tree

B-Tree is a self-balancing search tree. In most of the other self-balancing search trees (like AVL and Red-Black Trees), it is assumed that everything is in the main memory. 

To understand the use of B-Trees, we must think of the huge amount of data that cannot fit in the main memory. When the number of keys is high, the data is read from the disk in the form of blocks. Disk access time is very high compared to the main memory access time. The main idea of using B-Trees is to reduce the number of disk accesses. Most of the tree operations (search, insert, delete, max, min, ..etc ) require O(h) disk accesses where h is the height of the tree. B-tree is a fat tree. The height of B-Trees is kept low by putting the maximum possible keys in a B-Tree node. Generally, the B-Tree node size is kept equal to the disk block size. Since the height of the B-tree is low so total disk accesses for most of the operations are reduced significantly compared to balanced Binary Search Trees like AVL Tree, Red-Black Tree, etc.

Refer to this article to read about more on B+ Tree

6. Segment Tree

In computer science, a Segment Tree, also known as a statistic tree, is a tree data structure used for storing information about intervals, or segments. It allows querying which of the stored segments contain a given point. It is, in principle, a static structure; that is, it’s a structure that cannot be modified once it’s built. A similar data structure is the interval tree.

A segment tree for a set I of n intervals uses O(n log n) storage and can be built in O(n log n) time. Segment trees support searching for all the intervals that contain a query point in time O(log n + k), k being the number of retrieved intervals or segments.

Segment Tree

Refer to this article to read about more on Segment Tree