Level Order Traversal (Breadth First Search or BFS) of Binary Tree
Last Updated :
19 Apr, 2024
Level Order Traversal technique is defined as a method to traverse a Tree such that all nodes present in the same level are traversed completely before traversing the next level.
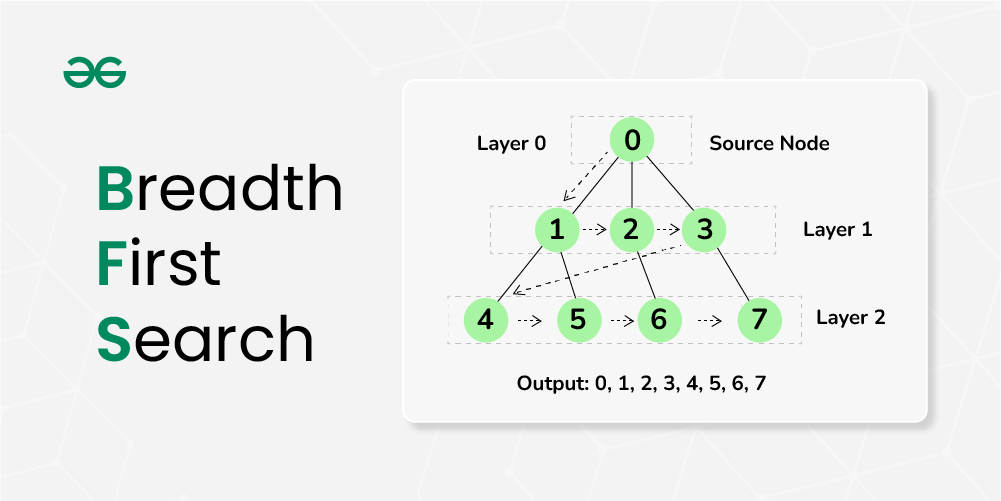
Example:
Input:
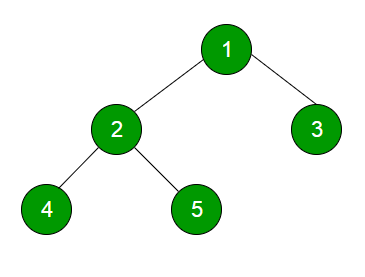
Output:
1
2 3
4 5
How does Level Order Traversal work?
The main idea of level order traversal is to traverse all the nodes of a lower level before moving to any of the nodes of a higher level. This can be done in any of the following ways:
- the naive one (finding the height of the tree and traversing each level and printing the nodes of that level)
- efficiently using a queue.
Level Order Traversal (Naive approach):
Find height of tree. Then for each level, run a recursive function by maintaining current height. Whenever the level of a node matches, print that node.
Below is the implementation of the above approach:
C++
// Recursive CPP program for level
// order traversal of Binary Tree
#include <bits/stdc++.h>
using namespace std;
// A binary tree node has data,
// pointer to left child
// and a pointer to right child
class node {
public:
int data;
node *left, *right;
};
// Function prototypes
void printCurrentLevel(node* root, int level);
int height(node* node);
node* newNode(int data);
// Function to print level order traversal a tree
void printLevelOrder(node* root)
{
int h = height(root);
int i;
for (i = 1; i <= h; i++)
printCurrentLevel(root, i);
}
// Print nodes at a current level
void printCurrentLevel(node* root, int level)
{
if (root == NULL)
return;
if (level == 1)
cout << root->data << " ";
else if (level > 1) {
printCurrentLevel(root->left, level - 1);
printCurrentLevel(root->right, level - 1);
}
}
// Compute the "height" of a tree -- the number of
// nodes along the longest path from the root node
// down to the farthest leaf node.
int height(node* node)
{
if (node == NULL)
return 0;
else {
// Compute the height of each subtree
int lheight = height(node->left);
int rheight = height(node->right);
// Use the larger one
if (lheight > rheight) {
return (lheight + 1);
}
else {
return (rheight + 1);
}
}
}
// Helper function that allocates
// a new node with the given data and
// NULL left and right pointers.
node* newNode(int data)
{
node* Node = new node();
Node->data = data;
Node->left = NULL;
Node->right = NULL;
return (Node);
}
// Driver code
int main()
{
node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
cout << "Level Order traversal of binary tree is \n";
printLevelOrder(root);
return 0;
}
// This code is contributed by rathbhupendra
// Recursive C program for level
// order traversal of Binary Tree
#include <stdio.h>
#include <stdlib.h>
// A binary tree node has data,
// pointer to left child
// and a pointer to right child
struct node {
int data;
struct node *left, *right;
};
// Function prototypes
void printCurrentLevel(struct node* root, int level);
int height(struct node* node);
struct node* newNode(int data);
// Function to print level order traversal a tree
void printLevelOrder(struct node* root)
{
int h = height(root);
int i;
for (i = 1; i <= h; i++)
printCurrentLevel(root, i);
}
// Print nodes at a current level
void printCurrentLevel(struct node* root, int level)
{
if (root == NULL)
return;
if (level == 1)
printf("%d ", root->data);
else if (level > 1) {
printCurrentLevel(root->left, level - 1);
printCurrentLevel(root->right, level - 1);
}
}
// Compute the "height" of a tree -- the number of
// nodes along the longest path from the root node
// down to the farthest leaf node
int height(struct node* node)
{
if (node == NULL)
return 0;
else {
// Compute the height of each subtree
int lheight = height(node->left);
int rheight = height(node->right);
// Use the larger one
if (lheight > rheight)
return (lheight + 1);
else
return (rheight + 1);
}
}
// Helper function that allocates a new node with the
// given data and NULL left and right pointers.
struct node* newNode(int data)
{
struct node* node
= (struct node*)malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
// Driver program to test above functions
int main()
{
struct node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
printf("Level Order traversal of binary tree is \n");
printLevelOrder(root);
return 0;
}
// Recursive Java program for level
// order traversal of Binary Tree
// Class containing left and right child of current
// node and key value
class Node {
int data;
Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
class BinaryTree {
// Root of the Binary Tree
Node root;
public BinaryTree() { root = null; }
// Function to print level order traversal of tree
void printLevelOrder()
{
int h = height(root);
int i;
for (i = 1; i <= h; i++)
printCurrentLevel(root, i);
}
// Compute the "height" of a tree -- the number of
// nodes along the longest path from the root node
// down to the farthest leaf node.
int height(Node root)
{
if (root == null)
return 0;
else {
// Compute height of each subtree
int lheight = height(root.left);
int rheight = height(root.right);
// use the larger one
if (lheight > rheight)
return (lheight + 1);
else
return (rheight + 1);
}
}
// Print nodes at the current level
void printCurrentLevel(Node root, int level)
{
if (root == null)
return;
if (level == 1)
System.out.print(root.data + " ");
else if (level > 1) {
printCurrentLevel(root.left, level - 1);
printCurrentLevel(root.right, level - 1);
}
}
// Driver program to test above functions
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
System.out.println("Level order traversal of"
+ "binary tree is ");
tree.printLevelOrder();
}
}
# Recursive Python program for level
# order traversal of Binary Tree
# A node structure
class Node:
# A utility function to create a new node
def __init__(self, key):
self.data = key
self.left = None
self.right = None
# Function to print level order traversal of tree
def printLevelOrder(root):
h = height(root)
for i in range(1, h+1):
printCurrentLevel(root, i)
# Print nodes at a current level
def printCurrentLevel(root, level):
if root is None:
return
if level == 1:
print(root.data, end=" ")
elif level > 1:
printCurrentLevel(root.left, level-1)
printCurrentLevel(root.right, level-1)
# Compute the height of a tree--the number of nodes
# along the longest path from the root node down to
# the farthest leaf node
def height(node):
if node is None:
return 0
else:
# Compute the height of each subtree
lheight = height(node.left)
rheight = height(node.right)
# Use the larger one
if lheight > rheight:
return lheight+1
else:
return rheight+1
# Driver program to test above function
if __name__ == '__main__':
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
print("Level order traversal of binary tree is -")
printLevelOrder(root)
# This code is contributed by Nikhil Kumar Singh(nickzuck_007)
// Recursive c# program for level
// order traversal of Binary Tree
using System;
// Class containing left and right
// child of current node and key value
public class Node {
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
class GFG {
// Root of the Binary Tree
public Node root;
public void BinaryTree() { root = null; }
// Function to print level order
// traversal of tree
public virtual void printLevelOrder()
{
int h = height(root);
int i;
for (i = 1; i <= h; i++) {
printCurrentLevel(root, i);
}
}
// Compute the "height" of a tree --
// the number of nodes along the longest
// path from the root node down to the
// farthest leaf node.
public virtual int height(Node root)
{
if (root == null) {
return 0;
}
else {
// Compute height of each subtree
int lheight = height(root.left);
int rheight = height(root.right);
// use the larger one
if (lheight > rheight) {
return (lheight + 1);
}
else {
return (rheight + 1);
}
}
}
// Print nodes at the current level
public virtual void printCurrentLevel(Node root,
int level)
{
if (root == null) {
return;
}
if (level == 1) {
Console.Write(root.data + " ");
}
else if (level > 1) {
printCurrentLevel(root.left, level - 1);
printCurrentLevel(root.right, level - 1);
}
}
// Driver Code
public static void Main(string[] args)
{
GFG tree = new GFG();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
Console.WriteLine("Level order traversal "
+ "of binary tree is ");
tree.printLevelOrder();
}
}
// This code is contributed by Shrikant13
// Recursive javascript program for level
// order traversal of Binary Tree
// Class containing left and right child of current
// node and key value
class Node {
constructor(val) {
this.data = val;
this.left = null;
this.right = null;
}
}
// Root of the Binary Tree
var root= null;
// Function to print level order traversal of tree
function printLevelOrder() {
var h = height(root);
var i;
for (i = 1; i <= h; i++)
printCurrentLevel(root, i);
}
// Compute the "height" of a tree -- the number
// of nodes along the longest path
// from the root node down to the farthest leaf node.
function height(root) {
if (root == null)
return 0;
else {
// Compute height of each subtree
var lheight = height(root.left);
var rheight = height(root.right);
// Use the larger one
if (lheight > rheight)
return (lheight + 1);
else
return (rheight + 1);
}
}
// Print nodes at the current level
function printCurrentLevel(root , level) {
if (root == null)
return;
if (level == 1)
console.log(root.data + " ");
else if (level > 1) {
printCurrentLevel(root.left, level - 1);
printCurrentLevel(root.right, level - 1);
}
}
// Driver program to test above functions
root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
console.log("Level order traversal of binary tree is ");
printLevelOrder();
// This code is contributed by umadevi9616
OutputLevel Order traversal of binary tree is
1 2 3 4 5
Time Complexity: O(N), where N is the number of nodes in the skewed tree.
Auxiliary Space: O(1) If the recursion stack is considered the space used is O(N).
Level Order Traversal using Queue
We need to visit the nodes in a lower level before any node in a higher level, this idea is quite similar to that of a queue. Push the nodes of a lower level in the queue. When any node is visited, pop that node from the queue and push the child of that node in the queue.
This ensures that the node of a lower level are visited prior to any node of a higher level.
Below is the Implementation of the above approach:
C++
// C++ program to print level order traversal
#include <bits/stdc++.h>
using namespace std;
// A Binary Tree Node
struct Node {
int data;
struct Node *left, *right;
};
// Iterative method to find height of Binary Tree
void printLevelOrder(Node* root)
{
// Base Case
if (root == NULL)
return;
// Create an empty queue for level order traversal
queue<Node*> q;
// Enqueue Root and initialize height
q.push(root);
while (q.empty() == false) {
// Print front of queue and remove it from queue
Node* node = q.front();
cout << node->data << " ";
q.pop();
// Enqueue left child
if (node->left != NULL)
q.push(node->left);
// Enqueue right child
if (node->right != NULL)
q.push(node->right);
}
}
// Utility function to create a new tree node
Node* newNode(int data)
{
Node* temp = new Node;
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
// Driver program to test above functions
int main()
{
// Let us create binary tree shown in above diagram
Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
cout << "Level Order traversal of binary tree is \n";
printLevelOrder(root);
return 0;
}
// Iterative Queue based C program
// to do level order traversal
// of Binary Tree
#include <stdio.h>
#include <stdlib.h>
#define MAX_Q_SIZE 500
// A binary tree node has data,
// pointer to left child
// and a pointer to right child
struct node {
int data;
struct node* left;
struct node* right;
};
// Function prototypes
struct node** createQueue(int*, int*);
void enQueue(struct node**, int*, struct node*);
struct node* deQueue(struct node**, int*);
// Given a binary tree, print its nodes in level order
// using array for implementing queue
void printLevelOrder(struct node* root)
{
int rear, front;
struct node** queue = createQueue(&front, &rear);
struct node* temp_node = root;
while (temp_node) {
printf("%d ", temp_node->data);
// Enqueue left child
if (temp_node->left)
enQueue(queue, &rear, temp_node->left);
// Enqueue right child
if (temp_node->right)
enQueue(queue, &rear, temp_node->right);
// Dequeue node and make it temp_node
temp_node = deQueue(queue, &front);
}
}
// Utility functions
struct node** createQueue(int* front, int* rear)
{
struct node** queue = (struct node**)malloc(
sizeof(struct node*) * MAX_Q_SIZE);
*front = *rear = 0;
return queue;
}
void enQueue(struct node** queue, int* rear,
struct node* new_node)
{
queue[*rear] = new_node;
(*rear)++;
}
struct node* deQueue(struct node** queue, int* front)
{
(*front)++;
return queue[*front - 1];
}
// Helper function that allocates a new node with the
// given data and NULL left and right pointers.
struct node* newNode(int data)
{
struct node* node
= (struct node*)malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
// Driver program to test above functions
int main()
{
struct node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
printf("Level Order traversal of binary tree is \n");
printLevelOrder(root);
return 0;
}
// Iterative Queue based Java program
// to do level order traversal
// of Binary Tree
import java.util.LinkedList;
import java.util.Queue;
// Class to represent Tree node
class Node {
int data;
Node left, right;
public Node(int item)
{
data = item;
left = null;
right = null;
}
}
// Class to print Level Order Traversal
class BinaryTree {
Node root;
// Given a binary tree. Print
// its nodes in level order
// using array for implementing queue
void printLevelOrder()
{
Queue<Node> queue = new LinkedList<Node>();
queue.add(root);
while (!queue.isEmpty()) {
// poll() removes the present head.
Node tempNode = queue.poll();
System.out.print(tempNode.data + " ");
// Enqueue left child
if (tempNode.left != null) {
queue.add(tempNode.left);
}
// Enqueue right child
if (tempNode.right != null) {
queue.add(tempNode.right);
}
}
}
public static void main(String args[])
{
// Creating a binary tree and entering
// the nodes
BinaryTree tree_level = new BinaryTree();
tree_level.root = new Node(1);
tree_level.root.left = new Node(2);
tree_level.root.right = new Node(3);
tree_level.root.left.left = new Node(4);
tree_level.root.left.right = new Node(5);
System.out.println("Level order traversal of binary tree is - ");
tree_level.printLevelOrder();
}
}
# Python program to print level
# order traversal using Queue
# A node structure
class Node:
# A utility function to create a new node
def __init__(self, key):
self.data = key
self.left = None
self.right = None
# Iterative Method to print the
# height of a binary tree
def printLevelOrder(root):
# Base Case
if root is None:
return
# Create an empty queue
# for level order traversal
queue = []
# Enqueue Root and initialize height
queue.append(root)
while(len(queue) > 0):
# Print front of queue and
# remove it from queue
print(queue[0].data, end=" ")
node = queue.pop(0)
# Enqueue left child
if node.left is not None:
queue.append(node.left)
# Enqueue right child
if node.right is not None:
queue.append(node.right)
# Driver Program to test above function
if __name__ == '__main__':
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
print("Level Order Traversal of binary tree is -")
printLevelOrder(root)
# This code is contributed by Nikhil Kumar Singh(nickzuck_007)
// Iterative Queue based C# program
// to do level order traversal
// of Binary Tree
using System;
using System.Collections.Generic;
// Class to represent Tree node
public class Node {
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = null;
right = null;
}
}
// Class to print Level Order Traversal
public class BinaryTree {
Node root;
// Given a binary tree. Print
// its nodes in level order using
// array for implementing queue
void printLevelOrder()
{
Queue<Node> queue = new Queue<Node>();
queue.Enqueue(root);
while (queue.Count != 0) {
Node tempNode = queue.Dequeue();
Console.Write(tempNode.data + " ");
// Enqueue left child
if (tempNode.left != null) {
queue.Enqueue(tempNode.left);
}
// Enqueue right child
if (tempNode.right != null) {
queue.Enqueue(tempNode.right);
}
}
}
// Driver code
public static void Main()
{
// Creating a binary tree and entering
// the nodes
BinaryTree tree_level = new BinaryTree();
tree_level.root = new Node(1);
tree_level.root.left = new Node(2);
tree_level.root.right = new Node(3);
tree_level.root.left.left = new Node(4);
tree_level.root.left.right = new Node(5);
Console.WriteLine("Level order traversal "
+ "of binary tree is - ");
tree_level.printLevelOrder();
}
}
// This code contributed by PrinciRaj1992
class Node {
constructor(val) {
this.data = val;
this.left = null;
this.right = null;
}
}
// Class to represent a deque (double-ended queue)
class Deque {
constructor() {
this.queue = [];
}
// Method to add an element to the end of the queue
enqueue(item) {
this.queue.push(item);
}
// Method to remove and return the first element of the queue
dequeue() {
return this.queue.shift();
}
// Method to check if the queue is empty
isEmpty() {
return this.queue.length === 0;
}
}
// Function to perform level order traversal of a binary tree
function printLevelOrder(root) {
// Create a deque to store nodes for traversal
const queue = new Deque();
// Add the root node to the queue
queue.enqueue(root);
// Continue traversal until the queue is empty
while (!queue.isEmpty()) {
// Remove and get the first node from the queue
const tempNode = queue.dequeue();
// Print the data of the current node
console.log(tempNode.data + " ");
// Enqueue the left child if it exists
if (tempNode.left !== null) {
queue.enqueue(tempNode.left);
}
// Enqueue the right child if it exists
if (tempNode.right !== null) {
queue.enqueue(tempNode.right);
}
}
}
// Create a binary tree and enter the nodes
const root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
// Print the level order traversal of the binary tree
console.log("Level order traversal of binary tree is - ");
printLevelOrder(root);
OutputLevel Order traversal of binary tree is
1 2 3 4 5
Time Complexity: O(N) where N is the number of nodes in the binary tree.
Auxiliary Space: O(N) where N is the number of nodes in the binary tree.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...