Angular Velocity Formula

Average angular velocity is defined as the ratio of angular displacement to the time taken by the object to undergo the displacement. It is denoted by ω_av.

                                                           ω_av = angular displacement / time travel

Consider the movement of a particle on a circular path with a centre at O.

Let us assume that in time Δt the particle displaces by an angle of Δθ.

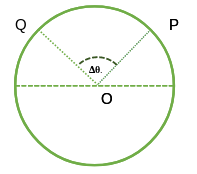
then the average angular velocity ω_av = Δθ/ Δt 

Since Δθ is scalar, average angular velocity is a scalar quantity.

Instantaneous angular velocity

It is the limiting value of the average angular velocity of the object in a small time interval, as the time interval approaches zero. It is denoted by ω.

ω = Lt_{t -> 0} Δθ/ Δt = dθ/dt 

Angular velocity is measured in radian per second and its unit is rad/s.

Since dθ is a vector, ω is also a vector.

Relation between angular velocity and linear velocity.

Linear velocity is the cross product of angular velocity and radius of the circular path.

v  =  ω x r

where,

v = linear velocity,

ω = angular velocity &

r = position vector from the centre of the circular path (radius).

The terms time period and frequency are synonymous with angular velocity, therefore it’s necessary to define them alongside angular velocity.

Time Period 

The time taken to complete one revolution or to displace by an angle of 2π radians is called time period and is denoted by T.   

as angular velocity ω is equal to  angular displacement/time, hence time period is related to angular velocity as 

ω = 2π/T

T = 2π/ω

Frequency 

The frequency of an object is the number of revolutions completed in a second. It is denoted by the Greek letter nu (ν).

ν = 1/T = ω/2π

Sample Problems

Problem 1: Calculate the angular velocity of the minute hand of a clock.

The minute hand completes one rotation in 60 minutes.

=> it displaces by 2π radians in 60*60 seconds

=> ω = 2π/3600 = 1.74 * 10^-3 rad/sec.

Problem 2: A ball is revolving in a circle of diameter 4 m with velocity 20 m/s find its angular velocity.

radius of circle = diameter/2 = 4/2 = 2m

linear velocity = 20 m/s

angular velocity = v / r

ω = 20 / 2 = 10 rad/sec

Problem 3: An object revolves in a horizontal circle of radius 12 m with a frequency of 4 hz. Find its linear speed.

Linear speed v = ω * r

frequency (f) = ω/2π

=> ω = 2π * f

=> v = 2π * f * r

=> v = 301.59 m/s.

Problem 4: An object has a constant angular velocity of 5 rad/s. What is its angular displacement in radians after 12 seconds?

Angular velocity = angular displacement/ time

=> angular displacement = angular velocity * time

=> angular displacement =  5 * 12 = 60 radians.